Lasketun kentän lisääminen Excelin pivot-taulukkoon
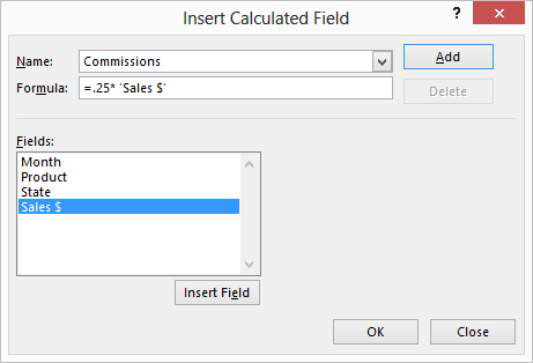
Tutustu, kuinka voit lisätä lasketun kentän Excelin pivot-taulukkoon ja laskea myynnistä syntyviä palkkioita tehokkaasti.
Useamman kuin kahden näytteen käyttäminen Excelissä: Kruskal-Wallis One-Way ANOVA
Excel osaa auttaa, kun näytteitä on enemmän kuin kaksi. FarKlemt Robotics, Inc. tutkii työntekijöilleen heidän tyytyväisyyttään työhönsä. He pyytävät kehittäjiä, johtajia, huoltotyöntekijöitä ja teknisiä kirjoittajia arvioimaan työtyytyväisyyttä asteikolla 1 (vähiten tyytyväinen) 100:aan (tyytyväisin).
Kussakin kategoriassa on kuusi työntekijää. Alla olevassa kuvassa on laskentataulukko, jossa on sarakkeiden A–D riveillä 1–7 olevat tiedot. Nollahypoteesi on, että kaikki näytteet ovat peräisin samasta populaatiosta. Vaihtoehtoinen hypoteesi on, että he eivät.
Kruskal-Wallis yksisuuntainen varianssianalyysi.
Sopiva ei-parametrinen testi on Kruskal-Wallis One-Way Variance-analyysi. Aloita asettamalla kaikki 24 pistettä nousevaan järjestykseen. Jälleen, jos nollahypoteesi pitää paikkansa, arvot tulisi jakaa suunnilleen tasaisesti ryhmiin.
Tämän tilaston kaava on
N on pisteiden kokonaismäärä ja n on kunkin ryhmän pisteiden määrä. Jotta asiat olisivat helppoja, määrität jokaiseen ryhmään saman määrän pisteitä, mutta se ei ole välttämätöntä tässä testissä. R on ryhmän sijoituksien summa. H jakautuu suunnilleen khin-neliöön, jossa df = ryhmien lukumäärä — 1, kun jokainen n on suurempi kuin 5.
Kuvaa taaksepäin katsottuna tietojen arvot ovat sarakkeiden A–D riveillä 9–15. Rivillä 16 on kunkin ryhmän sijoittelujen summat. Määritä N_Total solun F2 arvon nimeksi, tulosten kokonaismääräksi. Määritä n_ryhmä G2:n arvon nimeksi, kunkin ryhmän pisteiden lukumääräksi.
Laskeaksesi H , kirjoita
=(12/(N_Yhteensä*(N_Yhteensä+1)))*(SUMSQ(A16:D16)/n_ryhmä)-3*(N_Yhteensä+1)
soluun G6.
Kirjoita hypoteesitestiä varten
=CHISQ.JAKAUMA.RT(G6,3)
G7:ään. Tulos on pienempi kuin 0,05, joten hylkäät nollahypoteesin.
Microsoft Teamsin lataaminen, asentaminen ja avaaminen
Opi käyttämään Microsoft Teamsia: verkkopohjaista sovellusta, asiakkaana kannettavalla tietokoneella tai pöytätietokoneella tai Teams-mobiilisovellusta älypuhelimella tai tabletilla.
Kuinka estää Microsoft Wordia avaamasta tiedostoja vain luku -tilassa Windowsissa
Kuinka estää Microsoft Wordia avaamasta tiedostoja vain luku -tilassa Windowsissa Microsoft Word avaa tiedostot vain luku -tilassa, jolloin niiden muokkaaminen on mahdotonta? Älä huoli, menetelmät ovat alla
Microsoft Word -asiakirjojen virheellisen tulostuksen korjaaminen
Virheiden korjaaminen virheellisten Microsoft Word -asiakirjojen tulostuksessa. Virheet tulostettaessa Word-asiakirjoja, joissa on muuttuneet fontit, sotkuiset kappaleet, puuttuva teksti tai kadonnut sisältö ovat melko yleisiä. Älä kuitenkaan
Pyyhi kynä- ja korostuspiirrokset PowerPoint-dioistasi
Jos olet piirtänyt PowerPoint-dioihin esityksen aikana kynää tai korostuskynää, voit tallentaa piirustukset seuraavaa esitystä varten tai poistaa ne, jotta seuraavan kerran näytät ne. Aloitat puhtailla PowerPoint-dioilla. Pyyhi kynä- ja korostuskynäpiirrokset noudattamalla näitä ohjeita: Pyyhi rivit yksi kerrallaan […]
Tyylikirjaston sisältö SharePoint 2010:ssä
Tyylikirjasto sisältää CSS-tiedostoja, Extensible Stylesheet Language (XSL) -tiedostoja ja kuvia, joita käyttävät ennalta määritetyt sivupohjat, sivuasettelut ja säätimet SharePoint 2010:ssä. CSS-tiedostojen etsiminen julkaisusivuston tyylikirjastosta: Valitse Sivuston toiminnot→ Näytä Kaikki sivuston sisältö. Sivuston sisältö tulee näkyviin. Style-kirjasto sijaitsee […]
Muotoile numerot tuhansiksi ja miljooniksi Excel-raporteissa
Älä hukuta yleisöäsi jättimäisillä numeroilla. Microsoft Excelissä voit parantaa koontinäyttöjesi ja raporttiesi luettavuutta muotoilemalla numerot näyttämään tuhansia tai miljoonia.
SharePoint-sivustojen jakaminen ja seuraaminen
Opi käyttämään SharePointin sosiaalisen verkostoitumisen työkaluja, joiden avulla yksilöt ja ryhmät voivat kommunikoida, tehdä yhteistyötä, jakaa ja pitää yhteyttä.
Kuinka muuntaa päivämäärät Julian-muotoihin Excelissä
Juliaanisia päivämääriä käytetään usein valmistusympäristöissä aikaleimana ja pikaviitteenä eränumerolle. Tämän tyyppisen päivämääräkoodauksen avulla jälleenmyyjät, kuluttajat ja huoltoedustajat voivat tunnistaa tuotteen valmistusajankohdan ja siten tuotteen iän. Julian-päivämääriä käytetään myös ohjelmoinnissa, armeijassa ja tähtitiedessä. Erilainen […]
Access-verkkosovelluksen luominen
Voit luoda verkkosovelluksen Access 2016:ssa. Mikä verkkosovellus sitten on? No, verkko tarkoittaa, että se on verkossa, ja sovellus on vain lyhenne sanoista "sovellus". Mukautettu verkkosovellus on online-tietokantasovellus, jota käytetään pilvestä selaimen avulla. Rakennat ja ylläpidät verkkosovellusta työpöytäversiossa […]