Lasketun kentän lisääminen Excelin pivot-taulukkoon
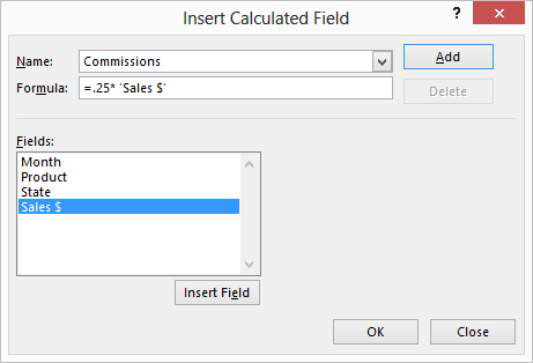
Tutustu, kuinka voit lisätä lasketun kentän Excelin pivot-taulukkoon ja laskea myynnistä syntyviä palkkioita tehokkaasti.
Mistä tiedät, onko ennustetrendi todellinen? Jos näet perusviivan, joka näyttää ajautuvan ylös tai alas, edustaako se todellista trendiä vai onko se vain satunnaista vaihtelua? Vastataksesi näihin kysymyksiin sinun on perehdyttävä todennäköisyyksiin ja tilastoihin. Onneksi sinun ei tarvitse mennä niihin liian pitkälle - ehkä ranteeseen asti.
Perusajatuksenkulku menee näin:
Käytä Exceliä kertoaksesi, mikä korrelaatio on myyntitulojen ja niihin liittyvien ajanjaksojen välillä.
Sillä ei ole väliä, edustanko ajanjaksoa tammikuussa 2011, helmikuussa 2011, maaliskuussa 2011 . . . joulukuuta 2016 tai 1., 2., 3. . . 72.
Jos tulojen ja ajanjakson välillä ei ole korrelaatiolla mitattua suhdetta, trendiä ei ole, eikä sinun tarvitse huolehtia siitä.
Jos on on suhde tulojen ja tiettyinä aikoina, sinun täytyy valita paras tapa käsitellä suuntaus.
Kun Excel on laskenut korrelaation, sinun on päätettävä, edustaako se todellista suhdetta ajanjakson ja tulon määrän välillä vai onko se vain onnenpotku.
Jos todennäköisyys, että se on vain onnea, on alle 5 prosenttia, se on todellinen trendi. (Ei myöskään 5 prosentissa mitään ihmeellistä – se on tavanomaista. Jotkut ihmiset käyttävät mieluummin yhtä prosenttia kriteerinä – se on konservatiivisempi kuin 5 prosenttia, ja he tuntevat olonsa hieman turvallisemmaksi.) Tämä nostaa esiin kysymyksen tilastollisesta merkitsevyydestä: mikä todennäköisyystaso tarvitsetko ennen kuin päätät, että jokin (tässä korrelaatio) on todellinen McCoy?
Korrelaatiokertoimen tilastollisen merkitsevyyden testaamiseen on olemassa erilaisia menetelmiä. Tässä on kolme suosittua menetelmää:
Muita suosittuja menetelmiä korrelaatiokertoimen tilastollisen merkitsevyyden testaamiseen on olemassa. Jokainen antaa hieman erilaisen tuloksen. Käytännössä teet melkein aina saman päätöksen (korrelaatio on tai ei eroa merkittävästi nollasta) riippumatta valitsemastasi menetelmästä.
Jos päätät, että korrelaatiomittausten trendi on todellinen (ja kun todennäköisyys, että korrelaatio on haamu, on alle 1 prosentti, sinun pitäisi luultavasti hyväksyä tämä johtopäätös), sinulla on vielä kaksi kysymystä kysyttäväsi itseltäsi:
Jos kilpailijan tulot putoavat samalla tavalla kuin sinun (tai jos molemmat tulot kasvavat), löydät todennäköisesti merkittävän korrelaation tulojesi ja kilpailijoiden välillä. Mutta on täysin mahdollista – jopa todennäköistä – että heidän tulojensa ja sinun tulojesi välillä ei ole todellista syy-yhteyttä. Saattaa olla, että sekä sinun että heidän omasi korreloivat todellisen syy-tekijän kanssa: kokonaismarkkinoiden koko muuttuu. Siinä tapauksessa sinun olisi todennäköisesti paljon parempi käyttää markkinoiden kokonaiskoon mittaa ennustemuuttujana. Tässä skenaariossa markkinoiden koolla on suora syy-yhteys tuloihisi, kun taas kilpailijoiden tuloilla on vain epäsuora suhde tuloihisi.
Tapa käsitellä tällainen tilanne on detrendoida molemmat muuttujat ensin muunnoksen avulla.
Tai voit mieluummin tehdä ennusteen käyttämällä lähestymistapaa, joka ei välttämättä käsittele trendejä hyvin, kuten liukuvat keskiarvot tai yksinkertainen eksponentiaalinen tasoitus. Yksi syy tähän on se, että saatat huomata, että tietojoukkosi regressiomenetelmä ei ole yhtä tarkka ennustaja kuin liukuvat keskiarvot tai tasoitus. Katso jälleen, voitko muuttaa tietoja trendin poistamiseksi.
Tutustu, kuinka voit lisätä lasketun kentän Excelin pivot-taulukkoon ja laskea myynnistä syntyviä palkkioita tehokkaasti.
Opi käyttämään Microsoft Teamsia: verkkopohjaista sovellusta, asiakkaana kannettavalla tietokoneella tai pöytätietokoneella tai Teams-mobiilisovellusta älypuhelimella tai tabletilla.
Kuinka estää Microsoft Wordia avaamasta tiedostoja vain luku -tilassa Windowsissa Microsoft Word avaa tiedostot vain luku -tilassa, jolloin niiden muokkaaminen on mahdotonta? Älä huoli, menetelmät ovat alla
Virheiden korjaaminen virheellisten Microsoft Word -asiakirjojen tulostuksessa. Virheet tulostettaessa Word-asiakirjoja, joissa on muuttuneet fontit, sotkuiset kappaleet, puuttuva teksti tai kadonnut sisältö ovat melko yleisiä. Älä kuitenkaan
Jos olet piirtänyt PowerPoint-dioihin esityksen aikana kynää tai korostuskynää, voit tallentaa piirustukset seuraavaa esitystä varten tai poistaa ne, jotta seuraavan kerran näytät ne. Aloitat puhtailla PowerPoint-dioilla. Pyyhi kynä- ja korostuskynäpiirrokset noudattamalla näitä ohjeita: Pyyhi rivit yksi kerrallaan […]
Tyylikirjasto sisältää CSS-tiedostoja, Extensible Stylesheet Language (XSL) -tiedostoja ja kuvia, joita käyttävät ennalta määritetyt sivupohjat, sivuasettelut ja säätimet SharePoint 2010:ssä. CSS-tiedostojen etsiminen julkaisusivuston tyylikirjastosta: Valitse Sivuston toiminnot→ Näytä Kaikki sivuston sisältö. Sivuston sisältö tulee näkyviin. Style-kirjasto sijaitsee […]
Älä hukuta yleisöäsi jättimäisillä numeroilla. Microsoft Excelissä voit parantaa koontinäyttöjesi ja raporttiesi luettavuutta muotoilemalla numerot näyttämään tuhansia tai miljoonia.
Opi käyttämään SharePointin sosiaalisen verkostoitumisen työkaluja, joiden avulla yksilöt ja ryhmät voivat kommunikoida, tehdä yhteistyötä, jakaa ja pitää yhteyttä.
Juliaanisia päivämääriä käytetään usein valmistusympäristöissä aikaleimana ja pikaviitteenä eränumerolle. Tämän tyyppisen päivämääräkoodauksen avulla jälleenmyyjät, kuluttajat ja huoltoedustajat voivat tunnistaa tuotteen valmistusajankohdan ja siten tuotteen iän. Julian-päivämääriä käytetään myös ohjelmoinnissa, armeijassa ja tähtitiedessä. Erilainen […]
Voit luoda verkkosovelluksen Access 2016:ssa. Mikä verkkosovellus sitten on? No, verkko tarkoittaa, että se on verkossa, ja sovellus on vain lyhenne sanoista "sovellus". Mukautettu verkkosovellus on online-tietokantasovellus, jota käytetään pilvestä selaimen avulla. Rakennat ja ylläpidät verkkosovellusta työpöytäversiossa […]