Lasketun kentän lisääminen Excelin pivot-taulukkoon
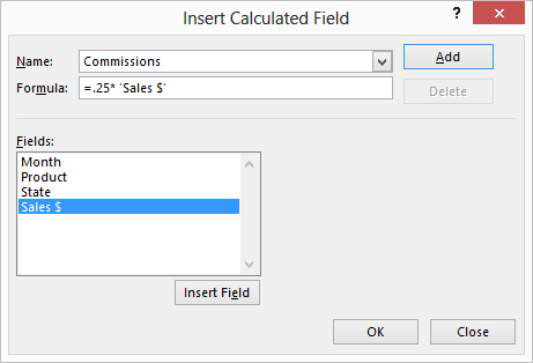
Tutustu, kuinka voit lisätä lasketun kentän Excelin pivot-taulukkoon ja laskea myynnistä syntyviä palkkioita tehokkaasti.
Kuinka löytää korrelaatio Excelissä
Spearmanin korrelaatiokerroin, rS, oli aikaisin arvoihin perustuva ei-parametrinen testi. Kun kyseessä on otos yksilöistä, jotka on mitattu kahdella Excelin muuttujalla, ideana on asettaa kukin pistemäärä omassa muuttujassaan. Sitten jokaisesta yksilöstä yksi arvo vähennetään toisesta. Jos korrelaatio on täydellinen (positiiviseen suuntaan), kaikki erot ovat nollia.
Alla olevassa kuvassa on esimerkki. Teollisuuspsykologi arvioi FarDrate Timepiece Corporationin 20 työntekijän sosiaalisuuden. Asteikko vaihteli 1:stä (vähiten seurallinen) 100:aan (seurallisin). Jokainen FarDraten työntekijä arvioi työtyytyväisyytensä myös asteikolla 1 (vähiten tyytyväisyys) 80:een (enin tyytyväisyys). Nollahypoteesi on, että sosiaalisuus ei korreloi työtyytyväisyyden kanssa. Vaihtoehtoinen hypoteesi on, että nämä kaksi muuttujaa korreloivat.
Tiedot ovat sarakkeissa B ja C, ja arvot ovat sarakkeissa E ja F. Kunkin riviparin erot ovat sarakkeessa G.
Spearmanin rS.
Kaava on
missä d on parien välinen ero. Kuten säännöllisen korrelaatiokertoimen tapauksessa, jos nollahypoteesi pitää paikkansa, rS:n arvon tulisi olla nollan tienoilla.
Laskeaksesi rivit sarakkeessa E, kirjoita
=RANK.AVG(B2,$B$2:$B$21,1)
E2:een ja täytetään automaattisesti. Kirjoita sarakkeen E riveille
=RANK.AVG(C2,$C$2:$C$21,1)
F2:een ja täytetään automaattisesti.
Sinun ei tarvitse kirjoittaa monimutkaista Excel-kaavaa soluun J4 laskeaksesi korrelaatiokertoimen. Miksi? Koska Excel ja matemaattiset tilastot yhdistävät yllätyksen: Sinun tarvitsee vain kirjoittaa
=KORREL(E2:E21,F2:F21)
kohtaan J4. Siinä kaikki. CORRELin käyttäminen riveissä antaa saman vastauksen kuin yllä oleva kaava. (Joten ei todellakaan ole tarpeen laskea parien välisiä arvoeroja sarakkeessa G.)
Laskea
N on parien lukumäärä ja testillä on N-2 vapausastetta.
Voit määrittää parien_määrä solun I2 arvon nimeksi. Joten kirjoita
=J4*SQRT(parien_määrä-2)/SQRT(1-J4^2)
J6:een ja
=T.JAKAUMA.2T(J6,parien_luku-2)
kohtaan J7. Voit käyttää kaksisuuntaista t-jakaumafunktiota, jos et tiedä korrelaation suuntaa etukäteen. Ja jälleen kerran, pieni p-arvo käskee hylätä nollahypoteesin.
Microsoft Teamsin lataaminen, asentaminen ja avaaminen
Opi käyttämään Microsoft Teamsia: verkkopohjaista sovellusta, asiakkaana kannettavalla tietokoneella tai pöytätietokoneella tai Teams-mobiilisovellusta älypuhelimella tai tabletilla.
Kuinka estää Microsoft Wordia avaamasta tiedostoja vain luku -tilassa Windowsissa
Kuinka estää Microsoft Wordia avaamasta tiedostoja vain luku -tilassa Windowsissa Microsoft Word avaa tiedostot vain luku -tilassa, jolloin niiden muokkaaminen on mahdotonta? Älä huoli, menetelmät ovat alla
Microsoft Word -asiakirjojen virheellisen tulostuksen korjaaminen
Virheiden korjaaminen virheellisten Microsoft Word -asiakirjojen tulostuksessa. Virheet tulostettaessa Word-asiakirjoja, joissa on muuttuneet fontit, sotkuiset kappaleet, puuttuva teksti tai kadonnut sisältö ovat melko yleisiä. Älä kuitenkaan
Pyyhi kynä- ja korostuspiirrokset PowerPoint-dioistasi
Jos olet piirtänyt PowerPoint-dioihin esityksen aikana kynää tai korostuskynää, voit tallentaa piirustukset seuraavaa esitystä varten tai poistaa ne, jotta seuraavan kerran näytät ne. Aloitat puhtailla PowerPoint-dioilla. Pyyhi kynä- ja korostuskynäpiirrokset noudattamalla näitä ohjeita: Pyyhi rivit yksi kerrallaan […]
Tyylikirjaston sisältö SharePoint 2010:ssä
Tyylikirjasto sisältää CSS-tiedostoja, Extensible Stylesheet Language (XSL) -tiedostoja ja kuvia, joita käyttävät ennalta määritetyt sivupohjat, sivuasettelut ja säätimet SharePoint 2010:ssä. CSS-tiedostojen etsiminen julkaisusivuston tyylikirjastosta: Valitse Sivuston toiminnot→ Näytä Kaikki sivuston sisältö. Sivuston sisältö tulee näkyviin. Style-kirjasto sijaitsee […]
Muotoile numerot tuhansiksi ja miljooniksi Excel-raporteissa
Älä hukuta yleisöäsi jättimäisillä numeroilla. Microsoft Excelissä voit parantaa koontinäyttöjesi ja raporttiesi luettavuutta muotoilemalla numerot näyttämään tuhansia tai miljoonia.
SharePoint-sivustojen jakaminen ja seuraaminen
Opi käyttämään SharePointin sosiaalisen verkostoitumisen työkaluja, joiden avulla yksilöt ja ryhmät voivat kommunikoida, tehdä yhteistyötä, jakaa ja pitää yhteyttä.
Kuinka muuntaa päivämäärät Julian-muotoihin Excelissä
Juliaanisia päivämääriä käytetään usein valmistusympäristöissä aikaleimana ja pikaviitteenä eränumerolle. Tämän tyyppisen päivämääräkoodauksen avulla jälleenmyyjät, kuluttajat ja huoltoedustajat voivat tunnistaa tuotteen valmistusajankohdan ja siten tuotteen iän. Julian-päivämääriä käytetään myös ohjelmoinnissa, armeijassa ja tähtitiedessä. Erilainen […]
Access-verkkosovelluksen luominen
Voit luoda verkkosovelluksen Access 2016:ssa. Mikä verkkosovellus sitten on? No, verkko tarkoittaa, että se on verkossa, ja sovellus on vain lyhenne sanoista "sovellus". Mukautettu verkkosovellus on online-tietokantasovellus, jota käytetään pilvestä selaimen avulla. Rakennat ja ylläpidät verkkosovellusta työpöytäversiossa […]