Lasketun kentän lisääminen Excelin pivot-taulukkoon
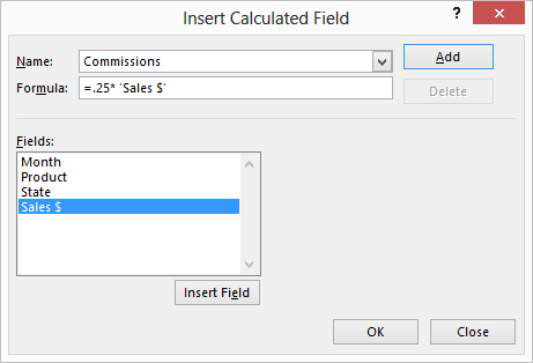
Tutustu, kuinka voit lisätä lasketun kentän Excelin pivot-taulukkoon ja laskea myynnistä syntyviä palkkioita tehokkaasti.
Excelissä binomijakaumien avulla voit laskea todennäköisyyksiä kahdessa tilanteessa. Lisäksi sinun tulee tuntea ainoa hypergeometrinen jakaumafunktio, koska se liittyy binomiaalisiin funktioihin. Käyttäisit binomijakaumia seuraavissa tilanteissa:
Kun sinulla on rajoitettu määrä riippumattomia kokeita tai testejä, jotka voivat joko onnistua tai epäonnistua
Kun jonkin kokeen onnistuminen tai epäonnistuminen on riippumaton muista kokeista
BINOM.JAKAUMA-funktio etsii binomiaalisen jakauman todennäköisyyden. Funktio käyttää syntaksia
=BINOM.JAKAUMA(numerot,kokeet,todennäköisyys_s,kumulatiivinen)
jossa luku_s on määritetty määrä onnistumisia, jotka haluat, kokeilut ovat tarkasteltavien kokeiden lukumäärää, probability_s on yhtä suuri kuin kokeilun onnistumisen todennäköisyys ja kumulatiivinen on kytkin, joka on asetettu joko loogiseen arvoon TOSI (jos haluat laskea kumulatiivisen todennäköisyyden) tai loogisen arvon EPÄTOSI (jos haluat laskea tarkan todennäköisyyden).
Esimerkiksi, jos kustantaja haluaa tietää todennäköisyyden julkaista kolme myydyintä kirjaa kymmenen kirjan sarjasta, kun myydyimmän kirjan julkaisun todennäköisyys on kymmenen prosenttia, kaava on
=BINOM.JAKAUMA(3;10;.1;EPÄTOSI)
joka palauttaa arvon. Tämä osoittaa, että on noin 6 prosentin todennäköisyys, että kustantaja julkaisee kymmenen kirjan sarjassa täsmälleen kolme myydyintä kirjaa.
Laskeaksesi todennäköisyyden, että kustantaja julkaisee joko yhden, kaksi tai kolme bestselleriä kymmenen kirjan sarjassa, kaava on
=BINOM.JAKAUMA(3;10;.1;TOSI)
joka palauttaa arvon , joka osoittaa, että on noin 99 prosentin todennäköisyys, että kustantaja julkaisee yhdestä kolmeen bestselleriä kymmenen kirjan sarjassa.
BINOM.INV-funktiot etsivät pienimmän arvon, jonka kumulatiivinen binomijakauma on yhtä suuri tai suurempi kuin määritetty kriteeri tai alfa-arvo. Funktio käyttää syntaksia
=BINOM.INV(kokeet,todennäköisyys_s,alfa)
jossa kokeet on yhtä suuri kuin tarkasteltavien Bernoulli-kokeiden lukumäärä, probability_s on kokeen onnistumisen todennäköisyys ja alfa on kriteerin arvo, jonka haluat täyttää tai voittaa.
Jos asetat kokeiden arvoksi 10, todennäköisyydeksi 0,5 ja kriteerin arvoksi 0,75, kaava on
=BINOM.INV(10;0,5;0,75)
joka palauttaa arvon 6.
BINOM.JAKAUMA.ALUE-funktio etsii koetuloksen todennäköisyyden tai kokeilutulosalueen binomijakauman osalta. Funktio käyttää syntaksia
=BINOM.JAKAUMA.ALUE(kokeet,todennäköisyys_s,luku_s,[luku_s2])
jossa kokeet on yhtä suuri kuin tarkasteltavien kokeiden lukumäärä, todennäköisyys_s on kokeen onnistumisen todennäköisyys, luku_s määrittää onnistuneiden kokeiden määrän ja luku_s2 (joka on valinnainen argumentti) määrittää onnistuneiden kokeiden enimmäismäärän.
Jos määrität kokeiden arvoksi 10, todennäköisyydeksi 0,5 ja onnistuneiden kokeiden lukumääräksi esimerkiksi 3, kaava on
=BINOM.JAKAUMA.ALUE(10;0.5;3)
joka palauttaa arvon 0,11718, mikä tarkoittaa, että täsmälleen kolmen onnistuneen kokeen todennäköisyys on noin 12 %.
Jos asetat kokeiden arvoksi 10, todennäköisyydeksi 0,5 ja onnistuneiden kokeiden määräksi esimerkiksi 3-10, kaava on
=BINOM.JAKAUMA.ALUE(10;0.5;3;10)
joka palauttaa arvon , mikä tarkoittaa, että onnistuneiden kokeiden lukumäärän todennäköisyys vaihtelee välillä 3–10, mikä vastaa noin 95 prosenttia.
NEGBINOM.JAKAUMA-funktio etsii todennäköisyyden, että tietty määrä epäonnistumisia tapahtuu ennen tiettyä määrää onnistumisia onnistumistodennäköisyysvakion perusteella. Funktio käyttää syntaksia
=NEGBINOM.JAKAUMA(luku_f,luku_s,todennäköisyys_s)
jossa luku_f on määritetty epäonnistumisten lukumäärä, luku_s on määritetty määrä onnistumisia, todennäköisyys_s on onnistumisen todennäköisyys ja kumulatiivinen on kytkin, jonka asetat arvoon 0 tai EPÄTOSI, jos haluat kumulatiivisen jakauman ja arvoon 1 tai TOSI, jos haluat todennäköisyysjakauma.
Oletetaan esimerkiksi, että olet villikissaöljyoperaattori ja haluat tietää mahdollisuuden, ettei öljyä löydy tasan kymmenestä kaivosta, ennen kuin löydät öljyä täsmälleen yhdestä kaivosta. Jos onnistumisen mahdollisuus on 5 prosenttia, voit löytää mahdollisuuden epäonnistumiseen kymmenen kertaa ennen kuin poraat ja etsit öljyä kaavan avulla
=NEGBINOM.JAKAUMA(10;2;.05;0)
joka palauttaa arvon 0,016465266, mikä osoittaa, että on alle 2 prosentin mahdollisuus, että epäonnistut kymmenen kertaa ennen kuin osut gusheriin.
CRITBINOM-funktio, joka on todella vanha Excel-toiminto ja joka on saatavilla Excelin uusimmissa versioissa taaksepäin yhteensopivuuden vuoksi, löytää pienimmän arvon, jonka kumulatiivinen binomijakauma on yhtä suuri tai suurempi kuin kriteerin arvo. Funktio käyttää syntaksia
=CRITBINOM(kokeet,todennäköisyys_s,alfa)
jossa kokeet on Bernoulli-kokeiden lukumäärä, todennäköisyys_s on kunkin kokeen onnistumisen todennäköisyys ja alfa on sama kuin kriteerisi arvo. Sekä probability_s- että alfa- argumenttien on oltava välillä 0 ja 1.
HYPERGEOMETRIA-funktio palauttaa todennäköisyyden tietylle määrälle näytteiden onnistumisia. Hypergeometrinen jakauma muistuttaa binomijakaumaa lukuun ottamatta hienovaraista eroa. Hypergeometrisessa jakaumassa menestys yhdessä kokeessa vaikuttaa menestykseen toisessa kokeessa. Yleensä käytät HYPGEOM.DIST-funktiota, kun otat näytteitä rajallisesta populaatiosta etkä vaihda näytteitä myöhempiä kokeita varten. Funktio käyttää syntaksia
=HYPGEOM.JAKAUMA(näytteen_määrät,näytteen_määrä,populaatiot,numeroponnahdus,kumulatiiviset)
jossa sample_s vastaa tietty määrä näytettä onnistumisia, number_sample antaa otoksen koko, population_s antaa onnistumisten lukumäärä väestössä, number_pop antaa väestön kokoa, ja kumulatiivinen on kytkin, joka kertoo Excel palauttaa joko kertymän (ilmaistu argumentin arvolla 1 tai TOSI) tai todennäköisyystiheydellä (ilmaistu argumentilla 0 tai EPÄTOSI).
Esimerkkinä hypergeometrisesta jakaumasta oletetaan, että haluat laskea todennäköisyyden, että 30 kohteen otoksesta 5 onnistuu. Oletetaan lisäksi, että tiedät, että 4 000 esineen väestöstä 1 000 menestyy. Käytät seuraavaa kaavaa tämän laskelman tekemiseen:
=HYPGEOM.JAKAUMA(5;30;1000;4000;0)
joka palauttaa arvon 0,0104596, mikä osoittaa, että todennäköisyys, että täsmälleen 5 kohdetta onnistuu 30 kohteen joukossa perusjoukon ominaisuuksien perusteella, on noin 10 prosenttia.
Tutustu, kuinka voit lisätä lasketun kentän Excelin pivot-taulukkoon ja laskea myynnistä syntyviä palkkioita tehokkaasti.
Opi käyttämään Microsoft Teamsia: verkkopohjaista sovellusta, asiakkaana kannettavalla tietokoneella tai pöytätietokoneella tai Teams-mobiilisovellusta älypuhelimella tai tabletilla.
Kuinka estää Microsoft Wordia avaamasta tiedostoja vain luku -tilassa Windowsissa Microsoft Word avaa tiedostot vain luku -tilassa, jolloin niiden muokkaaminen on mahdotonta? Älä huoli, menetelmät ovat alla
Virheiden korjaaminen virheellisten Microsoft Word -asiakirjojen tulostuksessa. Virheet tulostettaessa Word-asiakirjoja, joissa on muuttuneet fontit, sotkuiset kappaleet, puuttuva teksti tai kadonnut sisältö ovat melko yleisiä. Älä kuitenkaan
Jos olet piirtänyt PowerPoint-dioihin esityksen aikana kynää tai korostuskynää, voit tallentaa piirustukset seuraavaa esitystä varten tai poistaa ne, jotta seuraavan kerran näytät ne. Aloitat puhtailla PowerPoint-dioilla. Pyyhi kynä- ja korostuskynäpiirrokset noudattamalla näitä ohjeita: Pyyhi rivit yksi kerrallaan […]
Tyylikirjasto sisältää CSS-tiedostoja, Extensible Stylesheet Language (XSL) -tiedostoja ja kuvia, joita käyttävät ennalta määritetyt sivupohjat, sivuasettelut ja säätimet SharePoint 2010:ssä. CSS-tiedostojen etsiminen julkaisusivuston tyylikirjastosta: Valitse Sivuston toiminnot→ Näytä Kaikki sivuston sisältö. Sivuston sisältö tulee näkyviin. Style-kirjasto sijaitsee […]
Älä hukuta yleisöäsi jättimäisillä numeroilla. Microsoft Excelissä voit parantaa koontinäyttöjesi ja raporttiesi luettavuutta muotoilemalla numerot näyttämään tuhansia tai miljoonia.
Opi käyttämään SharePointin sosiaalisen verkostoitumisen työkaluja, joiden avulla yksilöt ja ryhmät voivat kommunikoida, tehdä yhteistyötä, jakaa ja pitää yhteyttä.
Juliaanisia päivämääriä käytetään usein valmistusympäristöissä aikaleimana ja pikaviitteenä eränumerolle. Tämän tyyppisen päivämääräkoodauksen avulla jälleenmyyjät, kuluttajat ja huoltoedustajat voivat tunnistaa tuotteen valmistusajankohdan ja siten tuotteen iän. Julian-päivämääriä käytetään myös ohjelmoinnissa, armeijassa ja tähtitiedessä. Erilainen […]
Voit luoda verkkosovelluksen Access 2016:ssa. Mikä verkkosovellus sitten on? No, verkko tarkoittaa, että se on verkossa, ja sovellus on vain lyhenne sanoista "sovellus". Mukautettu verkkosovellus on online-tietokantasovellus, jota käytetään pilvestä selaimen avulla. Rakennat ja ylläpidät verkkosovellusta työpöytäversiossa […]