Lasketun kentän lisääminen Excelin pivot-taulukkoon
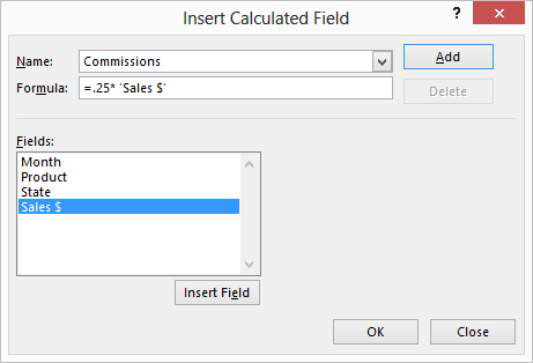
Tutustu, kuinka voit lisätä lasketun kentän Excelin pivot-taulukkoon ja laskea myynnistä syntyviä palkkioita tehokkaasti.
Tilastojen maailma on täynnä sudenkuoppia, mutta se on myös täynnä mahdollisuuksia. Olitpa tilastojen käyttäjä tai joku, jonka on tulkittava niitä, on mahdollista pudota sudenkuoppiin. Niiden ympärillä on myös mahdollista kävellä. Tässä on kymmenen vihjettä ja ansaa hypoteesien testaamisen, regression, korrelaation ja kaavion aloilta.
Merkitys on monella tapaa huonosti valittu termi. Kun tilastollinen testi tuottaa merkittävän tuloksen ja päätös on hylätä H0, se ei takaa, että tietojen taustalla oleva tutkimus on tärkeä. Tilastot voivat auttaa vain päätöksenteossa lukuja ja päätelmiä niistä prosesseista, jotka ovat tuottaneet ne. He eivät voi tehdä noista prosesseista tärkeitä tai maata mullistavia. Tärkeys on asia, jonka sinun on arvioitava itse – eikä mikään tilastollinen testi voi tehdä sitä puolestasi.
Kun regressiomallia yritetään sovittaa sirontakaavioon, houkutus on käyttää välittömästi suoraa. Tämä on parhaiten ymmärretty regressiomalli, ja kun saat siitä käsin, rinteet ja katkokset eivät ole niin pelottavia.
Mutta lineaarinen regressio ei ole ainoa regression muoto. On mahdollista sovittaa käyrä sirontakuvaajan läpi. Älä mene lankaan: Käyräviivaisen regression taustalla olevat tilastolliset käsitteet ovat vaikeampia ymmärtää kuin lineaarisen regression taustalla olevat käsitteet.
Näiden käsitteiden hallitsemiseen kannattaa kuitenkin varata aikaa. Joskus käyrä sopii paljon paremmin kuin viiva.
Työskenteletpä sitten lineaarisen tai kaarevan regression kanssa, muista, että ei ole tarkoituksenmukaista yleistää sirontakaavion rajojen ulkopuolelle.
Oletetaan, että olet luonut vankan ennustussuhteen matematiikan soveltuvuustestin ja matematiikan kurssien suorituskyvyn välille, ja sirontakaaviosi kattaa vain suppean matematiikan soveltuvuuden alueen. Et voi tietää, kestääkö suhde tämän alueen ulkopuolella. Tämän alueen ulkopuolella olevat ennusteet eivät kelpaa.
Paras vaihtoehto on laajentaa hajakuvaa testaamalla useampia ihmisiä. Saatat huomata, että alkuperäinen suhde kertoo vain osan tarinasta.
Jäännösten huolellinen analyysi (erot havaittujen ja ennustettujen arvojen välillä) voi kertoa paljon siitä, kuinka hyvin rivi sopii dataan. Perusoletus on, että vaihtelu regressioviivan ympärillä on sama ylös- ja alaspäin. Jos näin ei ole, malli ei ehkä ole niin ennustava kuin luulet. Jos vaihtelu on systemaattista (suurempi vaihtelu toisessa päässä kuin toisessa), käyräviivainen regressio saattaa olla sopivampi kuin lineaarinen. Arvioinnin keskivirhe ei aina ole indikaattori.
Usko tai älä, näin tapahtuu joskus korrelaatiokertoimien kanssa. Hyvin suuri otos voi tehdä pienestä korrelaatiokertoimesta tilastollisesti merkitsevän.
Mutta mitä tuo korrelaatiokerroin todella tarkoittaa? Determinaatiokerroin —r2 — on vain 0,038, mikä tarkoittaa, että SSRegressio on alle 4 prosenttia SSTtotalista. Se on hyvin pieni yhdistys.
Bottom line: Kun tarkastelet korrelaatiokerrointa, ota huomioon otoskoko. Jos se on tarpeeksi suuri, se voi saada triviaalin assosioinnin osoittautumaan tilastollisesti merkitseväksi. (Hmmm... merkitys – siinä se taas on!)
Kun katsot kaaviota, varmista, että tiedät, mitä kullakin akselilla on. Varmista, että ymmärrät mittayksiköt. Ymmärrätkö riippumattoman muuttujan? Ymmärrätkö riippuvaisen muuttujan? Voitko kuvailla jokaista omin sanoin? Jos vastaus johonkin näistä kysymyksistä on "Ei", et ymmärrä katsomaasi kaaviota.
Kun katsot kaaviota TV-mainoksessa, ole erittäin varovainen, jos se katoaa liian nopeasti, ennen kuin näet, mitä akseleilla on. Mainostaja saattaa yrittää luoda pysyvän väärän kuvan väärästä suhteesta kaavion sisällä. Graafinen suhde voi olla yhtä pätevä kuin muutkin TV-mainonnan osat – tieteellistä näyttöä piirretyllä sarjakuvalla: Pienet animoidut kuorintaharjat, jotka puhdistavat sarjakuvan hampaita, eivät välttämättä takaa sinulle valkoisempia hampaita, jos ostat tuotteen.
Joten olet juuri valmis kilpailemaan Rock-Paper-Scissors World Series -sarjassa. Valmistaudut tähän kansainväliseen turnaukseen, olet laskenut kaikki ottelusi viimeisen kymmenen vuoden ajalta ja listannut prosenttiosuuden, kuinka monta kertaa voitit pelatessasi jokaista roolia.
Voit tehdä yhteenvedon kaikista tuloksista luomalla kaavion Excelin grafiikkaominaisuuksien avulla.
Niin monet ihmiset luovat tällaisia kaavioita – ihmisiä, joiden pitäisi tietää paremmin. Kaavion viiva merkitsee jatkuvuutta pisteestä toiseen. Näillä tiedoilla se on tietysti mahdotonta. Mitä on kiven ja paperin välillä? Miksi ne ovat yhtä suuret yksiköt toisistaan? Miksi kolme luokkaa ovat tässä järjestyksessä?
Yksinkertaisesti sanottuna viivakaavio ei ole oikea kaavio, kun vähintään yksi muuttujistasi on joukko luokkia. Luo sen sijaan sarakekaavio. Ympyräkaavio toimii myös tässä, koska tiedot ovat prosentteja ja sinulla on vain muutama siivu.
Kun kaaviosi pisteet edustavat keskiarvoja, varmista, että kaavio sisältää kunkin keskiarvon keskivirheen. Tämä antaa katsojalle käsityksen tietojen vaihtelevuudesta – mikä on datan tärkeä näkökohta.
Keinot itsessään eivät aina kerro koko tarinaa. Käytä kaikki tilaisuus tutkia varianssit ja keskihajonnat. Saatat löytää piilotettuja kimpaleita. Systemaattinen vaihtelu – esimerkiksi suuriin keskiarvoihin liittyvät suuret varianssiarvot – saattaa olla vihje suhteesta, jota et nähnyt aiemmin.
Jos olet tosissaan tekemässä tilastotyötä, sinulla on luultavasti tilaisuus tutkia tilastotekstiä tai kaksi. Muista, että joidenkin tilastoalueiden symbolit eivät ole vakioita.
Oppikirjakäsitteiden yhdistäminen Excelin tilastotoimintoihin voi olla haaste tekstien ja Excelin takia. Viestit valintaikkunoissa ja ohjetiedostoissa voivat sisältää muita symboleja kuin ne, joista olet lukenut, tai ne voivat käyttää samoja symboleja, mutta eri tavalla. Tämä ristiriita saattaa johtaa siihen, että syötät väärän parametrin valintaikkunassa, mikä johtaa virheeseen, jota on vaikea jäljittää.
Tutustu, kuinka voit lisätä lasketun kentän Excelin pivot-taulukkoon ja laskea myynnistä syntyviä palkkioita tehokkaasti.
Opi käyttämään Microsoft Teamsia: verkkopohjaista sovellusta, asiakkaana kannettavalla tietokoneella tai pöytätietokoneella tai Teams-mobiilisovellusta älypuhelimella tai tabletilla.
Kuinka estää Microsoft Wordia avaamasta tiedostoja vain luku -tilassa Windowsissa Microsoft Word avaa tiedostot vain luku -tilassa, jolloin niiden muokkaaminen on mahdotonta? Älä huoli, menetelmät ovat alla
Virheiden korjaaminen virheellisten Microsoft Word -asiakirjojen tulostuksessa. Virheet tulostettaessa Word-asiakirjoja, joissa on muuttuneet fontit, sotkuiset kappaleet, puuttuva teksti tai kadonnut sisältö ovat melko yleisiä. Älä kuitenkaan
Jos olet piirtänyt PowerPoint-dioihin esityksen aikana kynää tai korostuskynää, voit tallentaa piirustukset seuraavaa esitystä varten tai poistaa ne, jotta seuraavan kerran näytät ne. Aloitat puhtailla PowerPoint-dioilla. Pyyhi kynä- ja korostuskynäpiirrokset noudattamalla näitä ohjeita: Pyyhi rivit yksi kerrallaan […]
Tyylikirjasto sisältää CSS-tiedostoja, Extensible Stylesheet Language (XSL) -tiedostoja ja kuvia, joita käyttävät ennalta määritetyt sivupohjat, sivuasettelut ja säätimet SharePoint 2010:ssä. CSS-tiedostojen etsiminen julkaisusivuston tyylikirjastosta: Valitse Sivuston toiminnot→ Näytä Kaikki sivuston sisältö. Sivuston sisältö tulee näkyviin. Style-kirjasto sijaitsee […]
Älä hukuta yleisöäsi jättimäisillä numeroilla. Microsoft Excelissä voit parantaa koontinäyttöjesi ja raporttiesi luettavuutta muotoilemalla numerot näyttämään tuhansia tai miljoonia.
Opi käyttämään SharePointin sosiaalisen verkostoitumisen työkaluja, joiden avulla yksilöt ja ryhmät voivat kommunikoida, tehdä yhteistyötä, jakaa ja pitää yhteyttä.
Juliaanisia päivämääriä käytetään usein valmistusympäristöissä aikaleimana ja pikaviitteenä eränumerolle. Tämän tyyppisen päivämääräkoodauksen avulla jälleenmyyjät, kuluttajat ja huoltoedustajat voivat tunnistaa tuotteen valmistusajankohdan ja siten tuotteen iän. Julian-päivämääriä käytetään myös ohjelmoinnissa, armeijassa ja tähtitiedessä. Erilainen […]
Voit luoda verkkosovelluksen Access 2016:ssa. Mikä verkkosovellus sitten on? No, verkko tarkoittaa, että se on verkossa, ja sovellus on vain lyhenne sanoista "sovellus". Mukautettu verkkosovellus on online-tietokantasovellus, jota käytetään pilvestä selaimen avulla. Rakennat ja ylläpidät verkkosovellusta työpöytäversiossa […]