Az f-eloszlások olyan valószínűségi eloszlások az Excelben, amelyek összehasonlítják a különböző sokaságokból vett minták szórásának arányát. Ez az összehasonlítás következtetést von le arra vonatkozóan, hogy az alapul szolgáló populációk eltérései hasonlítanak-e egymásra.
F.DIST: Balra irányú f-eloszlási valószínűség
Az F.ELOSZTÁS függvény azt a balra irányú valószínűséget adja vissza, hogy két minta eltérésének aránya akkora, mint egy megadott f-érték. A függvény a szintaxist használja
=F.DIST(x;szabadságfok1;szabadságfok2;halmozott)
ahol x a tesztelni kívánt f-érték; szabadságfok1 az első vagy számláló minta szabadsági fokai; A deg_freedom2 a szabadságfokok a másodikban, vagy a nevező, a minta, a kumulatív pedig egy logikai érték (0 vagy 1), amely megmondja az Excelnek, hogy a kumulatív eloszlást (ezt a kumulatív 0-ra állítja) vagy a valószínűségi sűrűséget ( a kumulatív 1-re állítása jelzi).
Tegyük fel, hogy összehasonlítja két minta varianciáját, az egyik egyenlő a másikkal egyenlő, mint például az F.DIST függvény működésére. Ez azt jelenti, hogy az f-érték egyenlő. Tegyük fel továbbá, hogy mindkét minta 10 elemből áll, ami azt jelenti, hogy mindkét minta szabadsági foka egyenlő, és kumulatív valószínűséget kíván kiszámítani. A képlet
=F.ELOSZTÁS(2/4;9;9;0)
a 0,6851816 értéket adja vissza.
F.DIST.RT: Jobboldali f-eloszlási valószínűség
Az F.DIST.RT funkció hasonlít az F.DIST funkcióra. Az F.DIST.RT azt a jobb oldali valószínűséget adja vissza, hogy két minta eltérésének aránya akkora, mint egy megadott f-érték. A függvény a szintaxist használja
=F.DIST.RT(x,szabadságfok1,szabadságfok2,halmozott)
ahol x a tesztelni kívánt f-érték; deg_freedom1 a szabadsági fokok az első, vagy a számláló, minta; A deg_freedom2 a szabadságfokok a másodikban, vagy a nevező, a minta, a kumulatív pedig egy logikai érték (0 vagy 1), amely megmondja az Excelnek, hogy a kumulatív eloszlást (ezt a kumulatív 0-ra állítja ) vagy a valószínűségi sűrűséget ( a kumulatív 1- re állítása jelzi ).
Példaként az F.DIST.RT függvény működésére, tegyük fel, hogy összehasonlítja két minta varianciáját, az egyik egyenlő a másikkal egyenlő. Ez azt jelenti, hogy az f-érték egyenlő. Tegyük fel továbbá, hogy mindkét minta 10 elemből áll, ami azt jelenti, hogy mindkét minta szabadsági foka egyenlő, és kumulatív valószínűséget kíván kiszámítani. A képlet
=F.ELOSZ.RT(2/4;9;9)
a 0,841761 értéket adja vissza, ami azt sugallja, hogy nagyjából 84 százalék a valószínűsége annak, hogy olyan nagy f-értéket észlel, mintha a minták eltérései ekvivalensek lennének.
F.INV: Balra irányú f-érték adott f-eloszlási valószínűséggel
Az F.INV függvény egy adott f-eloszlási valószínűségnek megfelelő balra irányú f-értéket adja vissza. A függvény a szintaxist használja
=F.INV(valószínűség,szabadságfok1,szabadságfok2)
ahol a valószínűség a megtalálni kívánt f érték valószínűsége; deg_freedom1 a szabadsági fokok az első, vagy a számláló, minta; és a deg_freedom2 a szabadságfokok a második vagy nevező mintában.
F.INV.RT:Jobbra irányú f-érték adott f-eloszlási valószínűséggel
Az F.INV.RT függvény egy adott f-eloszlási valószínűségnek megfelelő jobboldali f-értéket adja vissza. A függvény a szintaxist használja
=F.INV.RT(valószínűség,szabadságfok1,szabadságfok2)
ahol a valószínűség a megtalálni kívánt f-érték valószínűsége; deg_freedom1 a szabadsági fokok az első, vagy a számláló, minta; deg_freedom2 és a szabadságfokok a második vagy nevező mintában.
F.TESZT: A valószínűségi adatkészlet szórása nem különbözik
Az F.TEST függvény összehasonlítja két minta szórását, és visszaadja annak valószínűségét, hogy a szórások nem különböznek szignifikánsan. A függvény a szintaxist használja
=F.TESZT(tömb1;tömb2)
ahol a tömb1 az első mintát tartalmazó munkalap tartomány, és a második mintát tartalmazó munkalap tartomány.
Hogyan kell használni az F elosztási függvényt az Excelben?
Az F.DIST függvény használatának megértéséhez nézzünk meg egy példát:
Példa
Tegyük fel, hogy a következő adatokat kapjuk:
- Érték, amelyen a függvényt értékelni kívánjuk: 14.569
- Számoló szabadságfok: 4
- A szabadságfok nevezője: 2
Az F valószínűség meghatározásához a kumulatív eloszlásfüggvénnyel, amely az IGAZ kumulatív argumentum, a következő képletet használjuk:
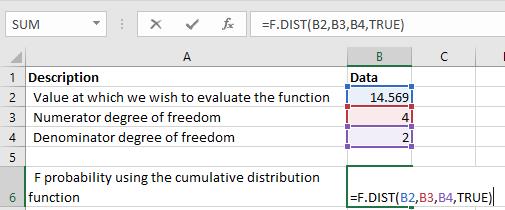
Az alábbi eredményt kapjuk:
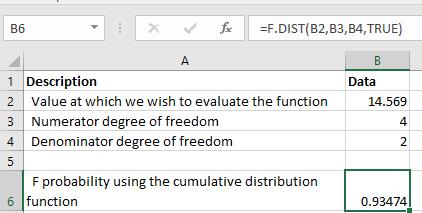
Az F valószínűség meghatározásához a valószínűségi sűrűségfüggvény segítségével, amely a HAMIS kumulatív argumentum, a következő képletet használjuk:
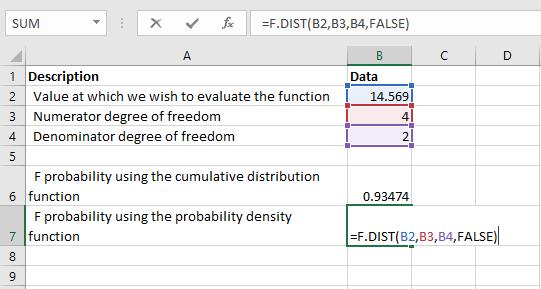
Az alábbi eredményt kapjuk:
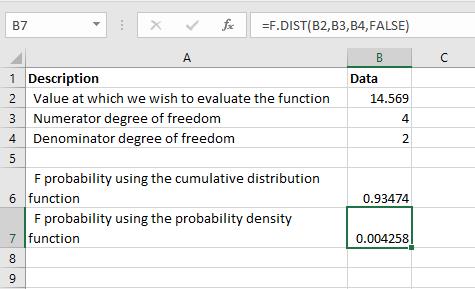
Amit emlékezni kell az F.DIST funkcióval kapcsolatban
- Ha a szabadságfok1 vagy a szabadságfok2 egy decimális szám, akkor az Excel egész számokra csonkolja.
- #SZÁM! hiba – Akkor fordul elő, ha valamelyik:
- Az x megadott értéke kisebb, mint 0.
- A szabadságfok1 vagy a szabadságfok2 értéke kisebb, mint 1.
- #ÉRTÉK! hiba – Akkor fordul elő, ha a megadott argumentumok bármelyike nem numerikus.