A Poisson nagyon hasznos eszköz lehet az Excel statisztikai elemzéséhez. Nem mutatja meg, hogyan működik? Íme az Excel POISSON.DIST használatának lépései:
Jelöljön ki egy cellát a POISSON.DIST válaszához.
A Statisztikai függvények menüben válassza ki a POISSON.DIST elemet a Függvényargumentumok párbeszédpanel megnyitásához.
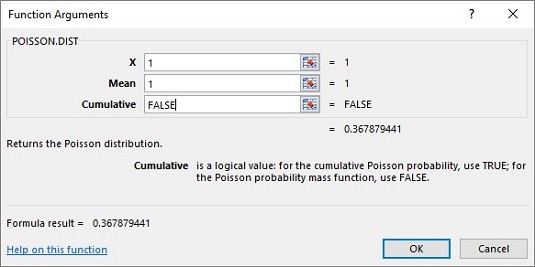
A Függvényargumentumok párbeszédpanelen adja meg az argumentumok megfelelő értékeit.
Az X mezőbe írja be azoknak az eseményeknek a számát, amelyek valószínűségét meghatározza. Ebben a példában a pr (1) értéket keresi , ezért írja be az 1-et.
Az Átlag mezőbe írja be a folyamat átlagát, ami ebben a példában 1.
A Kumulatív mezőben vagy IGAZ a kumulatív valószínűségre, vagy HAMIS, csak az események számának valószínűségére. Írja be a HAMIS.
Az X, Mean és Kumulative bejegyzésekkel a válasz megjelenik a párbeszédpanelen. A válasz erre a példára: .367879441.
Kattintson az OK gombra, hogy a választ a kijelölt cellába helyezze.
A példában a két hibás kötés valószínűségét 1000-ben, a valószínűségét pedig háromban látja. A számítások elvégzéséhez írja be a 2- t az X mezőbe a pr (2) kiszámításához , és a 3-at a pr (3) kereséséhez .
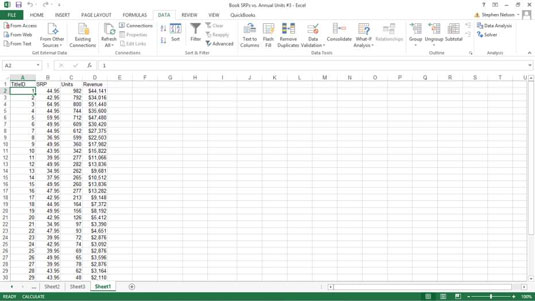
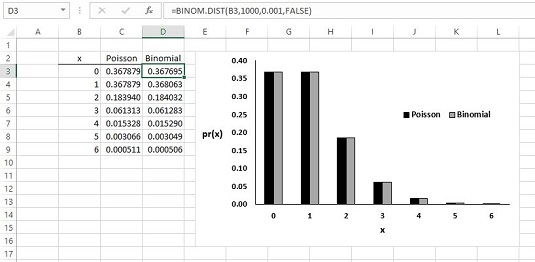
A 21. században nagyon könnyű közvetlenül kiszámítani a binomiális valószínűségeket. Az alábbi képen a Poisson és a binomiális valószínűségek láthatók a B oszlopban szereplő számokhoz, valamint a példa feltételei. A valószínűségek grafikonon vannak ábrázolva, így láthatja, mennyire közel áll a kettő valójában. A D3 cella lett kiválasztva, így a Képlet sáv megmutatja, hogyan használták a BINOM.DIST-t a binomiális valószínűségek kiszámításához.
Bár a Poisson-féle közelítés használhatósága elavult, önálló életet élt. Úgy tűnik, a Poisson-eloszlásokba illeszkednek az olyan széles körben eltérő jelenségek, mint a pszichológiai kísérletek reakcióidő-adatai, a radioaktív anyagok degenerációja és a professzionális jégkorongjátékok pontszámai. Az üzleti elemzők és tudományos kutatók ezért szeretnek erre az elosztásra alapozni a modelleket.
Lábjegyzetek és végjegyzetek létrehozása a Word 2013-ban. Részletes útmutató, hogyan készíthet különféle stílusú jegyzeteket bibliográfiai információkhoz vagy magyarázó megjegyzésekhez.
Tudjon meg mindent arról, hogyan lehet az Excelben kiemelni a statisztikailag kiugró értékeket, mégpedig egyszerű eszközökkel és módszerekkel. Kiemelt figyelmet fordítunk a kiugró értékek azonosítására és kezelésére.
Az Excel Mintavételi eszközével véletlenszerűen kiválaszthat elemeket egy adatkészletből vagy választhat minden n-edik elemet. Ismerje meg, hogyan használhatja ezt a hasznos funkciót az adatelemzéshez!
Fedezze fel a Microsoft Word 2019 legjobb trükkjeit, amelyek segítenek a hatékonyabb munkavégzésben. Tudd meg, hogyan használhatod ki a program funkcióit!
A Word 2019-ben a bekezdések igazítása és behúzása kulcsfontosságú a dokumentumok megfelelő megjelenítéséhez. Ismerje meg a formázási lehetőségeket és tippeket a hatékonyabb munkához.
Fedezze fel, hogyan használhatja az Excel 2019 Solver bővítményt a komplex problémák megoldására. A célcella, változócellák és kényszerek beállítása lépésről lépésre.
A Word lehetővé teszi dinamikus elemek hozzáadását a dokumentumhoz. Fedezze fel, hogyan lehet különböző mezőket használni a Word programban a dinamikus tartalom létrehozásához.
A SharePoint 2010 oszlopai az adatok tárolására szolgálnak. Fedezze fel a különböző oszlop típusokat és azok alkalmazását a SharePoint rendszeren belül.
A Word 2013 szövegtörlésének képessége kulcsfontosságú, legyen szó szövegalkotásról vagy törlésről. Ismerje meg a hatékony szövegtörlési módszereket!
A fotóalbum funkció a PowerPoint 2016-ban lehetővé teszi, hogy egyszerre több fényképet illesszen be egy prezentációba, megkönnyítve ezzel a többszörös képek kezelését.
