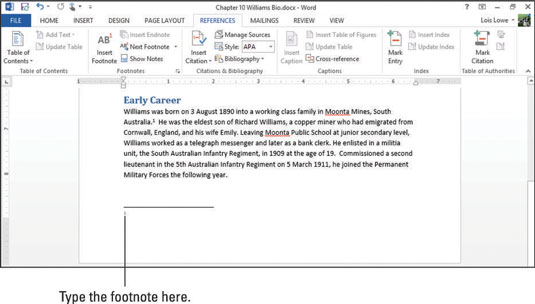
Az Excel 2016 PV (jelenérték), NPV (nettó jelenérték) és FV (jövő érték) függvényei a szalag Képletek lapján található Pénzügyi gomb legördülő menüjében (Alt+MI) lehetővé teszik a jövedelmezőség meghatározását. egy befektetésről.
A PV vagy jelenérték függvény egy befektetés jelenértékét adja vissza, amely az a teljes összeg, amelyet egy sor jövőbeli kifizetés jelenleg megér. A PV függvény szintaxisa a következő:
=PV(árfolyam,nper,pmt,[fv],[típus])
Az fv és type argumentumok nem kötelező argumentumok a függvényben (ezeket szögletes zárójelek jelzik). Az fv argumentum az a jövőbeli érték vagy készpénzegyenleg, amelyet az utolsó befizetése után szeretne megszerezni. Ha kihagyja az fv argumentumot, az Excel nulla (0) jövőbeli értéket vesz fel. A type argumentum jelzi, hogy a fizetés az időszak elején vagy végén történik-e: Írjon be 0-t (vagy hagyja ki a type argumentumot), ha a fizetés az időszak végén történik, és használja az 1-et, ha az időszak elején történik. a periódus.
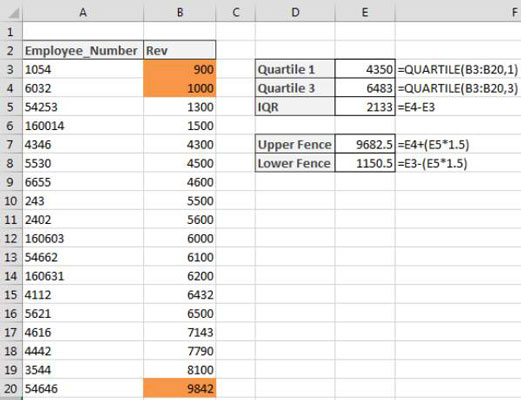
A következő ábra számos példát tartalmaz a PV függvény használatára. Mindhárom PV-funkció ugyanazt az 1,25 százalékos éves százalékarányt és 10 éves futamidőt alkalmaz. Mivel a kifizetések havonta történnek, minden funkció ezeket az éves adatokat havi adatokká alakítja át. Például az E3 cellában lévő PV függvényben az A3 cellában lévő éves kamatláb 12-vel osztva (A3/12) havi kamatlá alakul át. A B3 cellában lévő éves futamidőt 12-vel (B3 x 12) megszorozva egyenértékű havi időszakokká konvertáljuk.
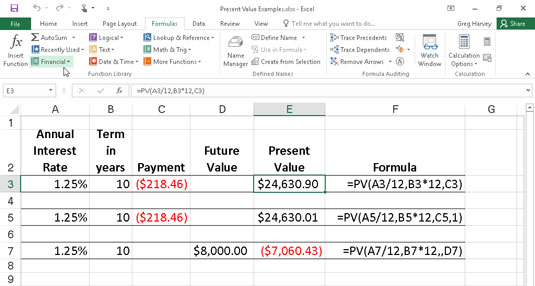
A PV függvénnyel a különféle befektetések jelenértékének kiszámításához.
Vegye figyelembe, hogy bár az E3 és E5 cellában lévő PV függvények a rate, nper és pmt (218,46 USD) argumentumot használják, eredményeik kissé eltérnek. Ezt a két függvény típus argumentumának különbsége okozza : az E3 cellában lévő PV függvény feltételezi, hogy minden fizetés az időszak végén történik (a type argumentum 0, ha kihagyjuk), míg a PV függvény Az E5 cella feltételezi, hogy minden kifizetés az időszak elején történik (ezt 1-es típusú argumentum jelzi ). Amikor a fizetést az időszak elején teljesítik, ennek a befektetésnek a jelenértéke 0,89 USD-vel magasabb, mint az időszak végén, tükrözve az elmúlt időszakban felhalmozott kamatot.
A harmadik példa az E7 cellában (a 4-1. ábrán látható) a PV függvényt használja fv argumentummal a pmt argumentum helyett . Ebben a példában a PV függvény azt állítja, hogy havi 7060,43 USD összegű befizetést kell fizetnie 10 éven keresztül, hogy elérje a 8000 USD készpénzegyenleget, feltételezve, hogy a befektetés állandó, 1 1/4 százalékos éves kamatlábat térített meg. Vegye figyelembe, hogy ha a PV függvényt az fv argumentummal használja a pmt argumentum helyett , akkor is vesszővel kell jeleznie a pmt argumentum pozícióját a függvényben (tehát a függvényben egymás után két vesszőt), hogy az Excel ne tévessze össze fv- érvét a pmt- érvvel.
Az NPV függvény a nettó jelenértéket a cash flow-k sorozata alapján számítja ki. Ennek a függvénynek a szintaxisa a következő
=NPV( arány , érték1 ,[ érték2 ],[...])
ahol az érték1, az érték2 és így tovább 1 és 13 érték közötti argumentum, amely kifizetések (negatív értékek) és bevételek (pozitív értékek) sorozatát képviseli, amelyek mindegyike időben egyenlő távolságra van és az időszak végén fordul elő. Az NPV befektetés egy periódussal az value1 cash flow időszaka előtt kezdődik, és az argumentumlista utolsó cash flow- jával ér véget. Ha az első pénzáramlás az időszak elején következik be, akkor ahelyett, hogy az egyik argumentumként szerepelne, hozzá kell adnia az NPV függvény eredményéhez.
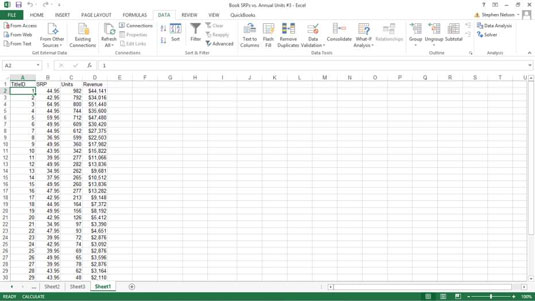
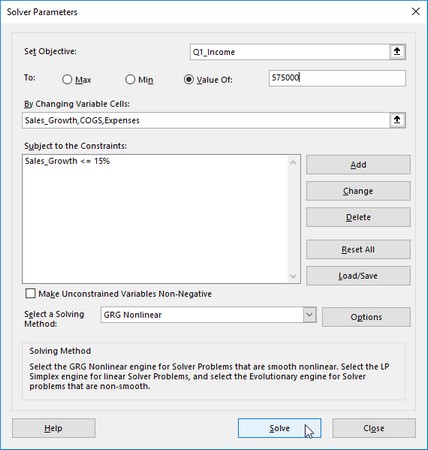
A következő ábra az NPV-függvény használatát szemlélteti egy 30 000 USD kezdeti befektetést igénylő ötéves befektetés vonzerejének értékelésére (a G3 cellában lévő érték). Az első évben 22 000 dollár veszteségre számít (B3 cella); a második évben 15 000 dollár nyereség (C3 cella); a harmadik évben 25 000 dollár nyereség (D3 cella); a negyedik évben 32 000 dollár nyereség (E3 cella); az ötödik évben pedig 38 000 dollár nyereség (F3 cella). Vegye figyelembe, hogy ezek a cellahivatkozások az NPV függvény érték argumentumaiként használatosak.
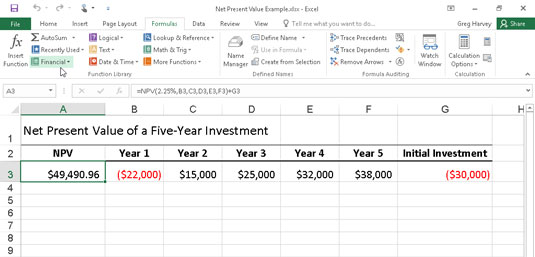
Az NPV függvény használata egy befektetés nettó jelenértékének kiszámításához.
A PV függvény használatával ellentétben az NPV függvény nem igényel egyenletes pénzáramlást. A függvény arány argumentuma 2,25 százalék. Ebben a példában ez a befektetés diszkontrátáját jelenti – vagyis azt a kamatlábat, amelyet az ötéves időszak során kaphat, ha pénzét más típusú befektetésbe, például magas hozamú pénzbe fekteti. -piaci számla. Ez az NPV-függvény az A3 cellában 49 490,96 dollár nettó jelenértéket ad vissza, ami azt jelzi, hogy sokkal több bevételre számíthat, ha 30 000 dollárját ebbe a befektetésbe fekteti, mint amennyit pénzpiaci számlára fektetne kamatláb mellett. 2,25 százalék.
Az FV függvény kiszámítja a befektetés jövőbeli értékét. Ennek a függvénynek a szintaxisa a következő
=FV(árfolyam,nper,pmt,[pv],[típus])
A rate, nper, pmt és type argumentumok megegyeznek a PV függvény által használtakkal. A pv argumentum az a jelenérték vagy átalányösszeg, amelynek jövőbeli értékét ki szeretné számítani. A PV függvény fv és type argumentumához hasonlóan az FV függvényben a pv és a type argumentumok is opcionálisak. Ha kihagyja ezeket az argumentumokat, az Excel a függvény értékét nullának (0) feltételezi.
Az FV függvény segítségével kiszámíthatja egy befektetés, például egy IRA (Individual Retirement Account) jövőbeli értékét. Tegyük fel például, hogy Ön 43 évesen létrehoz egy IRA-t, és 65 évesen 22 év múlva nyugdíjba megy, és minden év elején tervezi az IRA-ba történő éves befizetéseket. Ha évi 2,5 százalékos megtérülési rátát feltételez, akkor a következő FV függvényt kell beírnia a munkalapjába:
=FV(2,5%,22;-1500;,1)
Az Excel ekkor azt jelzi, hogy 44 376,64 USD jövőbeli értékre számíthat az IRA-ban, amikor 65 évesen nyugdíjba vonul. Ha egy évvel korábban létrehozta az IRA-t, és a számla jelenértéke már 1538 USD, akkor az FV függvényt a következőképpen kell módosítania. :
=FV(2,5%,22;–1500;–1538;1)
Ebben az esetben az Excel azt jelzi, hogy nyugdíjba vonuláskor 47 024,42 USD jövőbeli értékre számíthat az IRA-ban.
Hogyan lehet megakadályozni, hogy a Microsoft Word csak olvasható módban nyissa meg a fájlokat Windowson A Microsoft Word csak olvasható módban nyitja meg a fájlokat, így lehetetlenné teszi a szerkesztést? Ne aggódjon, a módszerek az alábbiakban találhatók
A nem megfelelő Microsoft Word dokumentumok nyomtatásának hibáinak kijavítása Meglehetősen gyakoriak a megváltozott betűtípusú, rendetlen bekezdésekkel, hiányzó szöveggel vagy elveszett tartalommal rendelkező Word dokumentumok nyomtatásának hibái. Azonban ne
Ha prezentáció közben a tollat vagy a kiemelőt használta a PowerPoint diákra való rajzoláshoz, mentheti a rajzokat a következő bemutatóhoz, vagy törölheti őket, így a következő bemutatáskor tiszta PowerPoint diákkal kezdheti. Kövesse az alábbi utasításokat a toll- és kiemelőrajzok törléséhez: A vonalak törlése egyenként […]
A Stíluskönyvtár CSS-fájlokat, XSL-fájlokat, valamint előre meghatározott mesteroldalak, oldalelrendezések és vezérlők által használt képeket tartalmaz a SharePoint 2010-ben. A CSS-fájlok megkereséséhez a közzétételi webhely stíluskönyvtárában: Válassza a Webhelyműveletek→Nézet lehetőséget. A webhely összes tartalma. Megjelenik az oldal tartalma. A Style könyvtár a […]
Ne árassza el közönségét óriási számokkal. A Microsoft Excelben javíthatja irányítópultjai és jelentései olvashatóságát, ha a számokat több ezerben vagy millióban formázza.
Ismerje meg, hogyan használhatja a SharePoints közösségi hálózati eszközöket, amelyek lehetővé teszik az egyének és csoportok közötti kommunikációt, együttműködést, megosztást és kapcsolódást.
A Julian-dátumokat gyártási környezetekben gyakran használják időbélyegként és gyors hivatkozásként a tételszámhoz. Az ilyen típusú dátumkódolás lehetővé teszi a kiskereskedők, fogyasztók és szervizek számára, hogy azonosítsák a termék elkészítésének időpontját, és ezáltal a termék korát. A Julian-dátumot a programozásban, a katonaságban és a csillagászatban is használják. Különböző […]
Létrehozhat webalkalmazást az Access 2016-ban. Tehát mi az a webalkalmazás? Nos, a web azt jelenti, hogy online van, az alkalmazás pedig az „alkalmazás” rövidítése. Az egyéni webalkalmazás egy online adatbázis-alkalmazás, amely a felhőből, böngészővel érhető el. Ön elkészíti és karbantartja a webalkalmazást az asztali verzióban […]
A SharePoint 2010 legtöbb oldala a navigációs hivatkozások listáját jeleníti meg az oldal bal oldalán található Gyorsindító sávon. A Gyorsindító sáv hivatkozásokat jelenít meg a kiemelt webhelytartalomra, például listákra, könyvtárakra, webhelyekre és közzétételi oldalakra. A Gyorsindító sáv két nagyon fontos hivatkozást tartalmaz: Az összes webhelytartalom linkje: A […]
Egyszerű problémák esetén az Excelben található Megoldó rendszerint gyorsan megtalálja a célfüggvény optimális Megoldóváltozó-értékeit. Bizonyos esetekben azonban a Solver nehezen találja meg a Solver változó értékeit, amelyek optimalizálják a célfüggvényt. Ezekben az esetekben a Solver általában egy üzenetet vagy hibaüzenetet jelenít meg, amely leírja vagy megvitatja a […]
