Az Excel egyes statisztikai mérőszámai nagyon zavaróak lehetnek, de a khi-négyzet függvények valóban praktikusak. Még akkor is, ha a khi-négyzet függvények közül csak az egyiket használja, olvassa el mindhárom függvényleírást. Statisztikai eszközök halmazaként tekintve a függvényeknek sokkal több értelme van.
A CHISQ.DIST.RT függvény, amely a khi-négyzet eloszlás jobboldali valószínűségét számítja ki, a khi-négyzet érték és a szabadságfokok felhasználásával számítja ki a szignifikanciaszintet. A khi-négyzet értéke egyenlő a standardizált pontszámok négyzetének összegével. A függvény a szintaxist használja
=CHISQ.DIST.RT( x , szabadságfok )
ahol x egyenlő a khi-négyzet értékével és a szabadság foka egyenlő a szabadságfokkal.
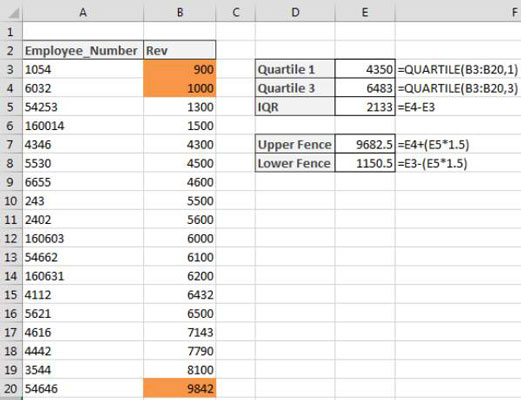
Példaként, hogy mindez hogyan működik, tegyük fel, hogy egy kicsit gyanakvóbb egy játékgép, amely a hat kép egyikét mutatja: gyémántok, csillagok, cowboycsizmák, cseresznyék, narancsok vagy aranyedények. Hat lehetőség esetén arra számíthat, hogy egy nagy mintában a hat lehetőség mindegyike nagyjából az esetek egyhatodában jelenik meg.
Tegyük fel, hogy a minta mérete például 180. Ebben az esetben arra számíthat, hogy minden játékgép-lehetőség 30-szor jelenik meg, mert 180/6 egyenlő 30-zal. Ha elkészített egy ilyen munkalaprészletet, elemezheti az egykarú banditát.
A szignifikanciaszint és a khi-négyzet eloszlásfüggvény kiszámításához a következő képletet írhatja be a D10-be:
=CHISQ.DIST.RT(D8,5)
A függvény a 0,010362338 értéket adja vissza, ami azt a szignifikanciaszintet jelenti, hogy a 15-ös khi-négyzet érték mintavételi hiba miatt következik be.
A D8 cella tartalmazza a khi-négyzet értéket, amely egyszerűen a megfigyelt és a várt értékek közötti különbség négyzetének összege. Például a D2 cellában lévő érték kiszámítása a =+(B2–C2)^2/C2 képlettel történik, így a 3,333333333 értéket kapja vissza. Előreláthatólag a D3:D7 tartományban lévő hasonló képletek kiszámítják a többi nyerőgép szimbólum négyzetes különbségét. És ó, mellesleg a D8 cellában a képlet =SZUM(D2:D7).
A lényeg: nem néz ki jól, igaz? Csak 1 százalék az esélye annak, hogy az Ön által aggódó nyerőgép a véletlennek köszönhetően valóban a megfigyelt értékeket produkálja. Nagyon gyanús.
A CHISQ.DIST függvény hasonlít a CHISQ.DIST.RT függvényre, de kiszámítja a khi-négyzet eloszlás balra irányú valószínűségét. A függvény a szintaxist használja
=CHISQ.DIST(x;szabadságfok;halmozott)
ahol x egyenlő a khí-négyzet értékével, a szabadság foka egyenlő a szabadságfokkal, a kumulatív pedig egy 0-ra vagy HAMIS értékre állított kapcsoló, ha valószínűségi sűrűséget szeretne kiszámítani, és 1-re vagy IGAZ-ra, ha kumulatív valószínűséget szeretne számítani.
A CHISQ.INV.RT függvény a khi-négyzet eloszlás jobboldali valószínűségének inverzét adja vissza. A függvény a szintaxist használja
=CHISQ.INV.RT(valószínűség,szabadságfok)
ahol a valószínűség egyenlő a szignifikancia szinttel és a deg_freedom egyenlő a szabadságfokkal.
A CHISQ.INV.RT függvény példájának bemutatásához tekintse meg a munkalaprészletet. Hat lehetséges kimenetel a nyerőgépen, akkor öt szabadsági foka van. Ezért, ha azt a khi-négyzetet szeretné kiszámítani, amely 0,010362338 szignifikanciaszintnek felel meg, akkor a következő képletet írja be a D12 cellába:
=CHISQ.INV.RT(D10,5)
Ez a függvény a 14,99996888 értéket adja vissza, ami nagyon közel áll a 15-höz. Vegye figyelembe, hogy a D10 az első valószínűségi argumentum, mivel ez a cella tartalmazza a CHISQ.DIST függvény által kiszámított szignifikanciaszintet.
A CHISQ.INV függvény a khi-négyzet eloszlás balra irányú valószínűségét adja vissza. A függvény a szintaxist használja
=CHISQ.INV(valószínűség,szabadságfok)
ahol a valószínűség egyenlő a szignifikancia szinttel és a deg_freedom egyenlő a szabadságfokkal.
A khi-négyzet értékének kiszámításához, amely egy 0,010362338 szignifikanciaszintnek felel meg 5 szabadságfokkal, beírhatja a következő képletet a munkalap egyik cellájába:
=CHISQ.INV(0,010362338,5)
Ez a függvény a .562927 értéket adja vissza.
A khi-négyzet tesztfüggvény segítségével felmérheti, hogy a megfigyelt és a várt értékek közötti különbségek véletlent vagy mintavételi hibát jelentenek-e . A függvény a szintaxist használja
=CHISQ.TESZT(tényleges_tartomány,várható_tartomány)
Ismét a gyanús nyerőgép példájára hivatkozva elvégezhet egy khi-négyzet tesztet úgy, hogy beírja a következő képletet a D14 cellába, majd összehasonlítja a megfigyelteket a várttal:
=CHISQ.TESZT(B2:B7,C2:C7)
A függvény a D14 cellában látható p-értéket vagy valószínűséget adja vissza, jelezve, hogy csak 1,0362 százalék az esélye annak, hogy a megfigyelt és a várt eredmények közötti különbségek mintavételi hibából fakadnak.
A khi-négyzet teszt közös jellemzője a p-érték – ismét a CHISQ.TEST függvény által visszaadott érték – szignifikanciaszinthez való összehasonlítása. Például a gyanús nyerőgép esetében azt mondhatja: „Mivel nem lehetünk 100 százalékosan biztosak, azt mondjuk, hogy 95 százalékos valószínűséget akarunk, ami 5 százalékos szintnek felel meg. jelentőség."
Ha a p-érték kisebb, mint a szignifikancia szintje, akkor azt feltételezi, hogy valami rossz. A statisztikusok, akik nem akarnak annyira földöntúlinak tűnni, van egy másik kifejezésük is erre a „valami hamis” következtetésre: a nullhipotézis elutasítása.
Lábjegyzetek és végjegyzetek létrehozása a Word 2013-ban. Részletes útmutató, hogyan készíthet különféle stílusú jegyzeteket bibliográfiai információkhoz vagy magyarázó megjegyzésekhez.
Tudjon meg mindent arról, hogyan lehet az Excelben kiemelni a statisztikailag kiugró értékeket, mégpedig egyszerű eszközökkel és módszerekkel. Kiemelt figyelmet fordítunk a kiugró értékek azonosítására és kezelésére.
Az Excel Mintavételi eszközével véletlenszerűen kiválaszthat elemeket egy adatkészletből vagy választhat minden n-edik elemet. Ismerje meg, hogyan használhatja ezt a hasznos funkciót az adatelemzéshez!
Fedezze fel a Microsoft Word 2019 legjobb trükkjeit, amelyek segítenek a hatékonyabb munkavégzésben. Tudd meg, hogyan használhatod ki a program funkcióit!
A Word 2019-ben a bekezdések igazítása és behúzása kulcsfontosságú a dokumentumok megfelelő megjelenítéséhez. Ismerje meg a formázási lehetőségeket és tippeket a hatékonyabb munkához.
Fedezze fel, hogyan használhatja az Excel 2019 Solver bővítményt a komplex problémák megoldására. A célcella, változócellák és kényszerek beállítása lépésről lépésre.
A Word lehetővé teszi dinamikus elemek hozzáadását a dokumentumhoz. Fedezze fel, hogyan lehet különböző mezőket használni a Word programban a dinamikus tartalom létrehozásához.
A SharePoint 2010 oszlopai az adatok tárolására szolgálnak. Fedezze fel a különböző oszlop típusokat és azok alkalmazását a SharePoint rendszeren belül.
A Word 2013 szövegtörlésének képessége kulcsfontosságú, legyen szó szövegalkotásról vagy törlésről. Ismerje meg a hatékony szövegtörlési módszereket!
A fotóalbum funkció a PowerPoint 2016-ban lehetővé teszi, hogy egyszerre több fényképet illesszen be egy prezentációba, megkönnyítve ezzel a többszörös képek kezelését.
