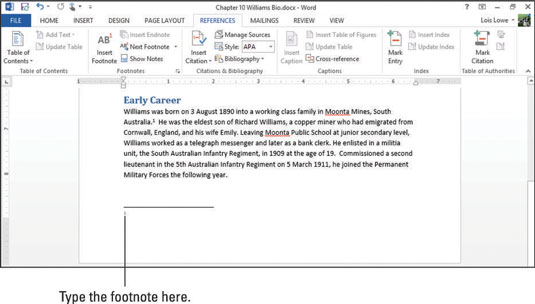
Az Excelben a binomiális eloszlások két helyzetben teszik lehetővé a valószínűségek kiszámítását. Ezenkívül ismernie kell az egyetlen hipergeometrikus eloszlásfüggvényt, mivel az binomiális függvényekhez kapcsolódik. Az alábbi helyzetekben binomiális eloszlásokat használjon:
Ha korlátozott számú független kísérlettel vagy teszttel rendelkezik, amelyek sikeresek vagy sikertelenek
Amikor egy próba sikere vagy kudarca független a többi kísérlettől
A BINOM.DIST függvény megkeresi a binomiális eloszlás valószínűségét. A függvény a szintaxist használja
=BINOM.ELOSZTÁS(számok_próbák,valószínűség_k,halmozott)
ahol a szám_s a kívánt sikerek meghatározott száma, a trials egyenlő a megtekintett kísérletek számával, a probability_s egyenlő a próba sikerének valószínűségével, a kumulatív pedig egy kapcsoló, amely vagy az IGAZ logikai értékre van állítva (ha kumulatív valószínűséget szeretne kiszámítani) vagy a HAMIS logikai értéket (ha a pontos valószínűséget szeretné kiszámítani).
Például, ha egy kiadó meg akarja tudni, mekkora valószínűséggel ad ki három legkelendőbb könyvet egy tíz könyvből, amikor a legkelendőbb könyv kiadásának valószínűsége tíz százalék, a képlet:
=BINOM.ELOSZTÁS(3;10;.1;HAMIS)
amely az értéket adja vissza. Ez azt jelzi, hogy nagyjából 6 százalék az esélye annak, hogy egy tíz könyvből álló sorozatban egy kiadó pontosan három legkelendőbb könyvet ad ki.
Annak a valószínűségének kiszámításához, hogy egy kiadó egy, kettő vagy három bestsellert ad ki egy tíz könyvből álló sorozatban, a képlet:
=BINOM.ELOSZTÁS(3;10;.1;IGAZ)
amely az értéket adja vissza, ami azt jelzi, hogy nagyjából 99 százalék az esélye annak, hogy egy kiadó tíz könyvből álló sorozatban egy-három bestsellert ad ki.
A BINOM.INV függvények megtalálják a legkisebb értéket, amelynek kumulatív binomiális eloszlása megegyezik vagy meghaladja a megadott feltételt, vagy alfa értéket. A függvény a szintaxist használja
=BINOM.INV(próbák,valószínűség_ok,alfa)
ahol a próba megegyezik a vizsgált Bernoulli-próbák számával, a valószínűség_s egyenlő a próba sikerének valószínűségével, az alfa pedig a teljesíteni kívánt vagy meghaladni kívánt kritériumértékkel.
Ha a kísérleteket 10-re állítja, akkor a valószínűséget 0,5-re, a kritérium értékét pedig 0,75-re, a képlet
=BINOM.INV(10;0,5;0,75)
ami a 6-os értéket adja vissza.
A BINOM.DIST.RANGE függvény megkeresi egy próba eredményének valószínűségét vagy egy binomiális eloszlás próbaeredmény-tartományát. A függvény a szintaxist használja
=BINOM.ELOSZ.TARTOMÁNY(próbák,valószínűség_s,szám_s,[szám_s2])
ahol a trials egyenlő a megtekintett próbák számával, a probability_s egyenlő a próba sikerének valószínűségével, a number_s a sikeres kísérletek számát, a number_s2 (ez egy opcionális argumentum) pedig a sikeres kísérletek maximális számát.
Ha a kísérleteket 10-re állítja, a valószínűséget 0,5-re, a sikeres kísérletek számát pedig 3-ra, akkor a képlet
=BINOM.ELTARTOMÁNY(10;0,5;3)
ami 0,11718 értéket ad vissza, ami azt jelenti, hogy annak valószínűsége, hogy pontosan három sikeres próba lesz, nagyjából 12%.
Ha a kísérleteket 10-re állítja, a valószínűséget 0,5-re, a sikeres kísérletek számát pedig 3 és 10 közötti értékre állítja be, a képlet
=BINOM.ELTARTOMÁNY(10;0.5;3;10)
amely az értéket adja vissza, ami azt jelenti, hogy a sikeres kísérletek számának valószínűsége 3 és 10 között van, nagyjából 95%-kal egyenlő.
A NEGBINOM.DIST függvény a siker valószínűségi állandója alapján megkeresi annak valószínűségét, hogy egy megadott számú meghibásodás bekövetkezik egy megadott számú siker előtt. A függvény a szintaxist használja
=NEGBINOM.DIST(szám_f,szám_s,valószínűség_s)
ahol number_f a megadott meghibásodások száma, number_s a megadott számú sikerek probability_s a siker valószínűsége, és a kumulatív egy kapcsolóval 0 vagy HAMIS, ha szeretne egy kumulatív eloszlás és 1 vagy IGAZ, ha szeretne egy Valószínűségi eloszlás.
Tegyük fel például, hogy Ön egy vadmacska-olajkezelő, és szeretné tudni, milyen esélye van annak, hogy pontosan tíz kútban nem talál olajat, mielőtt pontosan egy kútban talál olajat. Ha a siker esélye 5 százalék, akkor a képlet segítségével tízszer is megtalálhatja annak esélyét, hogy elbukik, mielőtt fúrna és olajat találna.
=NEGBINOM.ELOSZTÁS(10;2;.05;0)
amely a 0,016465266 értéket adja vissza, ami azt jelzi, hogy kevesebb, mint 2 százalék az esélye annak, hogy tízszer meghibásodik, mielőtt eltalálná a dagasztót.
A CRITBINOM függvény, amely valóban egy régi Excel-függvény, és visszafelé kompatibilitási okokból elérhető az Excel legújabb verzióiban, megkeresi azt a legkisebb értéket, amelynél a kumulatív binomiális eloszlás egyenlő vagy meghaladja a feltételértéket. A függvény a szintaxist használja
=CRITBINOM(próbák,valószínűség_k,alfa)
ahol vizsgálatokban a száma Bernoulli-kísérletsorozat, probability_s a siker valószínűsége az egyes tárgyalás, és az alfa értéke a meghatározott határértéket. Mind a probability_s és alfa érvek kell esni 0 és 1 közötti.
A HYPERGEOMETRIC függvény egy meghatározott számú sikeres minta valószínűségét adja vissza. A hipergeometrikus eloszlás binomiális eloszlásra hasonlít, kivéve egy finom eltérést. Hipergeometrikus eloszlásban az egyik próba sikere befolyásolja a másik próba sikerét. Általában akkor használja a HYPGEOM.DIST függvényt, amikor véges sokaságból vesz mintát, és nem cseréli le a mintákat a következő kísérletekhez. A függvény a szintaxist használja
=HYPGEOM.DIST(minta_s,minta_száma,populáció_szám,szám_pop,halmozott)
ahol sample_s megegyezik a meghatározott számú minta sikerek number_sample adja a minta méretét, population_s ad sikerek számát a lakosság körében, number_pop ad a méret a lakosság, és a kumulatív egy kapcsoló, amely megmondja, Excel visszatérni sem kumulatív eloszlás (1-es vagy IGAZ argumentumértékkel jelölve) vagy valószínűségi sűrűséggel (0 vagy HAMIS argumentumértékkel jelezve).
Tegyük fel, hogy egy hipergeometrikus eloszlásra példaként ki akarja számítani annak valószínűségét, hogy egy 30 elemből álló mintában 5 lesz sikeres. Tegyük fel továbbá, hogy tudja, hogy egy 4000 elemből álló populáción belül 1000 sikeres. A számításhoz a következő képletet használja:
=HYPGEOM.DIST(5;30;1000;4000;0)
ami a 0,0104596 értéket adja vissza, ami azt jelzi, hogy nagyjából 10 százalék az esélye annak, hogy egy 30 elemből álló halmazban pontosan 5 elem lesz sikeres, ha figyelembe vesszük a sokaság jellemzőit.
Lábjegyzetek és végjegyzetek létrehozása a Word 2013-ban. Részletes útmutató, hogyan készíthet különféle stílusú jegyzeteket bibliográfiai információkhoz vagy magyarázó megjegyzésekhez.
Tudjon meg mindent arról, hogyan lehet az Excelben kiemelni a statisztikailag kiugró értékeket, mégpedig egyszerű eszközökkel és módszerekkel. Kiemelt figyelmet fordítunk a kiugró értékek azonosítására és kezelésére.
Az Excel Mintavételi eszközével véletlenszerűen kiválaszthat elemeket egy adatkészletből vagy választhat minden n-edik elemet. Ismerje meg, hogyan használhatja ezt a hasznos funkciót az adatelemzéshez!
Fedezze fel a Microsoft Word 2019 legjobb trükkjeit, amelyek segítenek a hatékonyabb munkavégzésben. Tudd meg, hogyan használhatod ki a program funkcióit!
A Word 2019-ben a bekezdések igazítása és behúzása kulcsfontosságú a dokumentumok megfelelő megjelenítéséhez. Ismerje meg a formázási lehetőségeket és tippeket a hatékonyabb munkához.
Fedezze fel, hogyan használhatja az Excel 2019 Solver bővítményt a komplex problémák megoldására. A célcella, változócellák és kényszerek beállítása lépésről lépésre.
A Word lehetővé teszi dinamikus elemek hozzáadását a dokumentumhoz. Fedezze fel, hogyan lehet különböző mezőket használni a Word programban a dinamikus tartalom létrehozásához.
A SharePoint 2010 oszlopai az adatok tárolására szolgálnak. Fedezze fel a különböző oszlop típusokat és azok alkalmazását a SharePoint rendszeren belül.
A Word 2013 szövegtörlésének képessége kulcsfontosságú, legyen szó szövegalkotásról vagy törlésről. Ismerje meg a hatékony szövegtörlési módszereket!
A fotóalbum funkció a PowerPoint 2016-ban lehetővé teszi, hogy egyszerre több fényképet illesszen be egy prezentációba, megkönnyítve ezzel a többszörös képek kezelését.
