Az Excel nagyszerű eszköz, amikor statisztikákat kell használni. Ha még soha nem volt kitéve statisztikai adatokkal az iskolában, vagy már egy-két évtizede volt, ezek a tippek segítenek az Excel által biztosított statisztikai eszközök használatában.
Az első dolog, amit tudnod kell, hogy néhány statisztikai elemzés és néhány statisztikai mérőszám átkozottul egyszerű. A leíró statisztikák, amelyek magukban foglalják például a pivot tábla kereszttáblázatait, valamint néhány statisztikai függvényt, még azok számára is értelmesek, akik nem annyira kvantitatívak.
Amikor valaki az átlag kifejezést használja , általában a leggyakoribb átlagmérésre utal, ami egy átlag. Ha megértjük, hogy az átlag kifejezés pontatlan, az Excel statisztikai funkcióinak nagy része érthetőbbé válik.
A megbeszélés konkrétabbá tételéhez tegyük fel, hogy egy kis értékkészletet néz: 1, 2, 3, 4 és 5. Mint azt talán tudja, az átlag ebben a kis értékkészletben 3. Kiszámolhatja az átlagot úgy, hogy összeadjuk a halmaz összes számát (1+2+3+4+5), majd ezt az összeget (15) elosztjuk a halmaz összes értékével (5).
A medián érték az az érték, amely elválasztja a legnagyobb értékeket a legkisebb értékektől. Az 1., 2., 3., 4. és 5. adatkészletben a medián 3. A 3. érték elválasztja a legnagyobb értékeket (4 és 5) a legkisebb értékektől (1 és 2).
Nem kell értenie a különböző átlagméréseket, de emlékeznie kell arra, hogy az átlag kifejezés meglehetősen pontatlan.
A szórásra vonatkozó képlet és a logika meglehetősen könnyen érthető.
A szórás azt írja le, hogy egy adathalmaz értékei hogyan változnak az átlag körül. A statisztikai mérőszámok, például a szórás ügyes vonása, hogy gyakran valódi betekintést nyerhet a vizsgált adatok jellemzőibe. A másik dolog az, hogy ezzel a két adatbittel gyakran lehet következtetéseket levonni az adatokra a minták alapján.
A megfigyelés az egyik olyan kifejezés, amellyel találkozni fog, ha bármit olvas a statisztikákról. A megfigyelés csak megfigyelés. A megfigyelés fogalmának meghatározásának egyik módja a következő: Valahányszor ténylegesen értéket rendelünk valamelyik valószínűségi változóhoz, megfigyelést hozunk létre.
A minta egy populációból származó megfigyelések gyűjteménye. Például, ha létrehoz egy adatkészletet, amely rögzíti a napi magas hőmérsékletet a környéken, akkor a megfigyelések kis gyűjteménye egy minta.
Ehhez képest a minta nem sokaság. Egy populáció magában foglalja az összes lehetséges megfigyelést.
Ha egy sokaságból vett értékmintát néz meg, és a minta reprezentatív és elég nagy, akkor a minta jellemzői alapján következtetéseket vonhat le a sokaságról.
A következtetéses statisztikák, bár nagyon erősek, két tulajdonsággal rendelkeznek, amelyeket tudnia kell:
Pontossági problémák
Meredek tanulási görbe
A P robability eloszlási függvény elég trükkösen hangzik; de valójában intuitív módon megértheti, mi az a valószínűségi eloszlási függvény, néhány hasznos példával.
Az egyik gyakori eloszlás, amelyről a statisztikai osztályokban hall, például a T eloszlás. A T eloszlás lényegében normális eloszlás, kivéve a nehezebb, kövérebb farok esetén.
Egy közös valószínűségi eloszlásfüggvény az egyenletes eloszlás. Egy egyenletes eloszlású, minden esetben ugyanaz valószínűséggel fordulnak elő. Az az egyedülálló ebben a disztribúcióban, hogy minden rohadt szinten van.
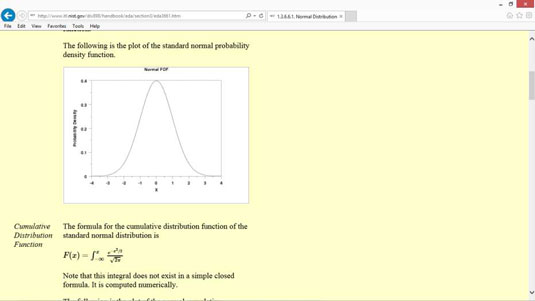
A valószínűségi eloszlásfüggvény másik gyakori típusa a normális eloszlás, más néven haranggörbe vagy Gauss-eloszlás.
A normális eloszlás sok esetben természetesen előfordul. Például az intelligencia hányadosok (IQ) normálisan oszlanak el.
A paraméter a valószínűségi eloszlási függvény bemenete. Más szavakkal, a valószínűségi eloszlási görbét leíró képlet, függvény vagy egyenlet bevitelt igényel. A statisztikákban ezeket a bemeneteket paramétereknek nevezzük.
Egyes valószínűségi eloszlási függvényekhez egyetlen egyszerű paraméterre van szükség. Például ahhoz, hogy egységes eloszlással dolgozhassunk, valójában csak az adatkészletben lévő értékek számára van szükség. Egy hatoldalú kocka például csak hat lehetőséget kínál.
Néhány további hasznos statisztikai kifejezés, amelyet tudnia kell, a ferdeség és a görbület. A ferdeség számszerűsíti a szimmetria hiányát a valószínűségi eloszlásban. Tökéletesen szimmetrikus eloszlásban a normál eloszláshoz hasonlóan a ferdeség nullával egyenlő. Ha azonban egy valószínűségi eloszlás jobbra vagy balra dől, akkor a ferdeség nullától eltérő értékkel egyenlő, és az érték számszerűsíti a szimmetria hiányát.
A Kurtosis számszerűsíti a farok nehézségét egy eloszlásban. Normál eloszlásban a kurtosis nulla. A farok az a dolog, amely balra vagy jobbra nyúlik. Ha azonban egy eloszlásban egy farok nehezebb, mint egy normál eloszlás, akkor a kurtózis pozitív szám. Ha egy eloszlásban a farok vékonyabb, mint a normál eloszlásban, akkor a körtózis negatív szám.
A valószínűségek gyakran összezavarják az embereket. A megbízhatósági szintekkel kapcsolatban fontos megérteni, hogy összefüggenek a hibahatárral.
Egy másik fontos dolog, amit meg kell érteni a megbízhatósági szintekkel kapcsolatban, hogy minél nagyobb a mintaméret, annál kisebb a hibahatár ugyanazt a megbízhatósági szintet használja.
Csak egy példaként, mondjuk, hogy rendelkezett néhány Google Analytics-adattal két különböző internetes hirdetésről, amelyeket kisvállalkozása népszerűsítése érdekében futtat, és szeretné tudni, melyik hirdetés a hatékonyabb. Használhatja a konfidenciaintervallum képletét annak meghatározására, hogy mennyi ideig kell futniuk a hirdetéseknek, mielőtt a Google elegendő adatot gyűjtött össze ahhoz, hogy megtudja, melyik hirdetés a jobb.
Lábjegyzetek és végjegyzetek létrehozása a Word 2013-ban. Részletes útmutató, hogyan készíthet különféle stílusú jegyzeteket bibliográfiai információkhoz vagy magyarázó megjegyzésekhez.
Tudjon meg mindent arról, hogyan lehet az Excelben kiemelni a statisztikailag kiugró értékeket, mégpedig egyszerű eszközökkel és módszerekkel. Kiemelt figyelmet fordítunk a kiugró értékek azonosítására és kezelésére.
Az Excel Mintavételi eszközével véletlenszerűen kiválaszthat elemeket egy adatkészletből vagy választhat minden n-edik elemet. Ismerje meg, hogyan használhatja ezt a hasznos funkciót az adatelemzéshez!
Fedezze fel a Microsoft Word 2019 legjobb trükkjeit, amelyek segítenek a hatékonyabb munkavégzésben. Tudd meg, hogyan használhatod ki a program funkcióit!
A Word 2019-ben a bekezdések igazítása és behúzása kulcsfontosságú a dokumentumok megfelelő megjelenítéséhez. Ismerje meg a formázási lehetőségeket és tippeket a hatékonyabb munkához.
Fedezze fel, hogyan használhatja az Excel 2019 Solver bővítményt a komplex problémák megoldására. A célcella, változócellák és kényszerek beállítása lépésről lépésre.
A Word lehetővé teszi dinamikus elemek hozzáadását a dokumentumhoz. Fedezze fel, hogyan lehet különböző mezőket használni a Word programban a dinamikus tartalom létrehozásához.
A SharePoint 2010 oszlopai az adatok tárolására szolgálnak. Fedezze fel a különböző oszlop típusokat és azok alkalmazását a SharePoint rendszeren belül.
A Word 2013 szövegtörlésének képessége kulcsfontosságú, legyen szó szövegalkotásról vagy törlésről. Ismerje meg a hatékony szövegtörlési módszereket!
A fotóalbum funkció a PowerPoint 2016-ban lehetővé teszi, hogy egyszerre több fényképet illesszen be egy prezentációba, megkönnyítve ezzel a többszörös képek kezelését.
