Създаване и управление на шаблони за Word 2019
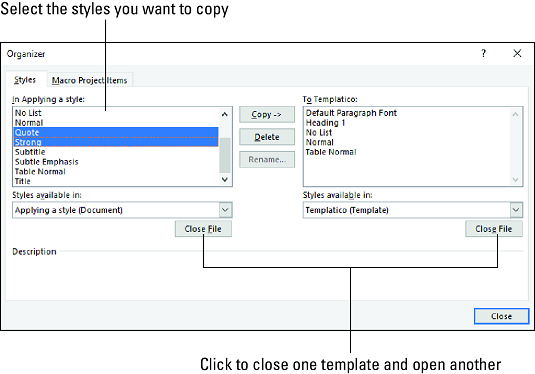
Научете как да създавате и управлявате шаблони за Word 2019 с нашето ръководство. Оптимизирайте документите си с персонализирани стилове.
Как да разберете дали дадена прогнозна тенденция е реална? Ако видите базова линия, която изглежда, че се движи нагоре или надолу, това представлява ли реална тенденция или е просто произволна вариация? За да отговорите на тези въпроси, трябва да влезете в вероятността и статистиката. За щастие, не е нужно да навлизате в тях твърде далеч - може би до китката.
Основният ход на мисли върви така:
Използвайте Excel, за да ви каже каква е връзката между приходите от продажби и свързаните с тях периоди от време.
Няма значение дали представям този период като януари 2011 г., февруари 2011 г., март 2011 г. . . декември 2016 г. или като 1, 2, 3 . . . 72.
Ако няма връзка, измерена чрез корелацията, между приходите и периода от време, няма тенденция и не е нужно да се притеснявате за това.
Ако има е връзката между приходите и периоди от време, трябва да се избере най-добрият начин да се справят с тази тенденция.
След като Excel изчисли корелацията, трябва да решите дали тя представлява реална връзка между периода от време и размера на приходите, или е просто късмет.
Ако вероятността това да е просто късмет е по-малка от 5 процента, това е реална тенденция. (Нищо вълшебно за 5 процента също — конвенционално е. Някои хора предпочитат да използват 1 процент като свой критерий — той е по-консервативен от 5 процента и се чувстват малко по-сигурни.) Това повдига въпроса за статистическата значимост: какво ниво на вероятност имате ли нужда, преди да решите, че нещо (тук, корелация) е истинският Маккой?
Съществуват различни методи за тестване на статистическата значимост на коефициента на корелация. Ето три популярни метода:
Съществуват и други популярни методи за тестване на статистическата значимост на коефициента на корелация. Всеки връща малко по-различен резултат. На практика почти винаги ще взимате едно и също решение (корелацията е или не е значително различна от нула), независимо от метода, който изберете.
Ако заключите, че тенденцията на корелационните мерки е реална (и когато вероятността е по-малка от 1 процент, че корелацията е призрак, вероятно трябва да приемете това заключение), имате още два въпроса, които да си зададете:
Ако приходите на конкуренцията намаляват като вашите (или ако и двата набора от приходи растат), ще откриете вероятно значителна корелация между вашите приходи и тези на конкуренцията. Но е напълно възможно — дори вероятно — да няма реална причинно-следствена връзка между техните приходи и вашите. Възможно е и вашето, и тяхното да са свързани с истинския причинно-следствен фактор: Размерът на цялостния пазар се променя. В този случай вероятно ще бъде много по-добре да използвате мярка за общия размер на пазара като променлива за прогнозиране. В този сценарий размерът на пазара има пряка, причинно-следствена връзка с вашите приходи, докато приходите на вашата конкуренция имат само непряка връзка с вашите приходи.
Начинът за справяне с този вид ситуация е първо да се отклонят и двете променливи чрез трансформация.
Или може да предпочетете да направите прогнозата си, като използвате подход, който не е задължително да се справя добре с тенденциите, като пълзящи средни или просто експоненциално изглаждане. Една от причините да направите това е, че може да откриете, че регресионният подход с вашия набор от данни не е толкова точен прогнозист, колкото пълзящите средни или изглаждането. Отново вижте дали можете да трансформирате данните, за да премахнете тенденцията.
Научете как да създавате и управлявате шаблони за Word 2019 с нашето ръководство. Оптимизирайте документите си с персонализирани стилове.
Научете как да настроите отстъп на абзаци в Word 2016, за да подобрите визуалната комуникация на вашите документи.
Как да блокирам Microsoft Word да отваря файлове в режим само за четене в Windows Microsoft Word отваря файлове в режим само за четене, което прави невъзможно редактирането им? Не се притеснявайте, методите са по-долу
Как да коригирате грешки при отпечатването на неправилни документи на Microsoft Word Грешките при отпечатването на документи на Word с променени шрифтове, разхвърляни абзаци, липсващ текст или изгубено съдържание са доста чести. Въпреки това недейте
Ако сте използвали писалката или маркера, за да рисувате върху слайдовете на PowerPoint по време на презентация, можете да запазите чертежите за следващата презентация или да ги изтриете, така че следващия път, когато го покажете, да започнете с чисти слайдове на PowerPoint. Следвайте тези инструкции, за да изтриете чертежи с писалка и маркери: Изтриване на линии една в […]
Библиотеката със стилове съдържа CSS файлове, файлове с разширяем език на стиловия език (XSL) и изображения, използвани от предварително дефинирани главни страници, оформления на страници и контроли в SharePoint 2010. За да намерите CSS файлове в библиотеката със стилове на сайт за публикуване: Изберете Действия на сайта→Преглед Цялото съдържание на сайта. Появява се съдържанието на сайта. Библиотеката Style се намира в […]
Не затрупвайте аудиторията си с огромни числа. В Microsoft Excel можете да подобрите четливостта на вашите табла за управление и отчети, като форматирате числата си така, че да се показват в хиляди или милиони.
Научете как да използвате инструменти за социални мрежи на SharePoint, които позволяват на индивиди и групи да общуват, да си сътрудничат, споделят и да се свързват.
Юлианските дати често се използват в производствени среди като времеви печат и бърза справка за партиден номер. Този тип кодиране на дата позволява на търговците на дребно, потребителите и обслужващите агенти да идентифицират кога е произведен продуктът и по този начин възрастта на продукта. Юлианските дати се използват и в програмирането, военните и астрономията. Различно […]
Можете да създадете уеб приложение в Access 2016. И така, какво всъщност е уеб приложение? Е, уеб означава, че е онлайн, а приложението е просто съкращение от „приложение“. Персонализирано уеб приложение е онлайн приложение за база данни, достъпно от облака с помощта на браузър. Вие създавате и поддържате уеб приложението в настолната версия […]








