Kombinatorisk analys med hjälp av Power Query i LuckyTemplates

Jag vill göra en djupdykning i något som kallas kombinatorisk analys. Detta kan definieras som att välja och arrangera delar av uppsättningar i enlighet med föreskrivna regler. Det kan låta esoteriskt, men det har faktiskt några väldigt praktiska användningsfall. Du kan se hela videon av denna handledning längst ner på den här bloggen.

I den här handledningen kommer jag att visa dig hur du gör detta med hjälp av Power Query i LuckyTemplates.

Innehållsförteckning

• Exempelfall för kombinatorisk analys
• Kombinatorisk analys: Permutationer i Power Query
• Kombinatorisk analys: Kombinationer i Power Query
• Slutsats

Exempelfall för kombinatorisk analys

I detta exempel på kombinatorisk analys var uppgiften att vi hade en lista med sex lager och vi behövde generera varje unik uppsättning av tre. Det låter som ett ganska okomplicerat problem, men det här är ett av de fall där språket verkligen betyder något.

Det korrekta svaret här är antingen 216, 120, 56 eller 20. Så, beroende på hur du definierar den unika uppsättningen och reglerna du ordinerat, kan du bli av med en faktor 10 om du inte får uppsättningen korrekt.

Och så, det är två dimensioner som betyder något här. Den första är " spelar ordning någon roll ?" Så när vi pratar om tre uppsättningar av tre, är ABC ekvivalent med BCA? Så spelar ordning roll? Och om ordning spelar någon roll så pratar vi om permutationer .

Ett bra exempel på permutationer där ordning kan ha betydelse är (vi pratar om ett lagersammanhang) när det gäller restid. Det kan mycket väl vara så att om du besöker lager A, sedan lager B och sedan lager C, så kan restiden på grund av trafikflöde med trafik mot trafik, tiden då du anlände till varje lager, vara ganska olika beroende på beställning där du besöker dem.

Baksidan av det är " ordning spelar ingen roll ", i vilket fall vi pratar om kombinationer , inte permutationer. Användningsfallet här som är vanligt är avstånd. Till exempel, fågelvägen kommer avståndet från A till B till C inte att vara annorlunda än avståndet från B till C till A. Dessa kommer att betraktas i ett kombinationssammanhang.

Kombinationer anses vara dubbletter av varandra. Medan de i ett permutationssammanhang anses vara unika.

Och så, som du kan se, borde ett kombinationslås verkligen vara ett permutationslås för i så fall spelar ordning roll, vilket gör det till en permutation, inte en kombination.

Den andra frågan eller dimensionen som är viktig är " när en vara har plockats, kan den plockas igen? " Om vi ​​till exempel väljer A som vårt första lager, kan vi välja A igen, eller måste vi välja unika element varje gång?

Termen vi använder här är " med ersättning " eller " utan ersättning ". Så om en vara kan plockas igen, är det med ersättning, vilket innebär att du väljer den. Och på sätt och vis går den tillbaka till urvalsbehållaren och plockas igen. Om svaret är nej, är det utan ersättning.

Och så kan du se i den här lösningen att permutationer med ersättning är de minst restriktiva. Så det är den som ger oss 216 unika set. Och kombinationer utan ersättning är den mest restriktiva och ger oss 20.

Vi kommer bara att använda dessa formler som ett sätt att kontrollera våra resultat. Så vi kommer ihåg 216, 120, 56 och 20. Låt oss nu hoppa in i Power Query och se hur denna kombinatoriska analys utspelar sig.

Kombinatorisk analys: Permutationer i Power Query

I Power Query har jag här ett mycket enkelt fall med sex namngivna lager.

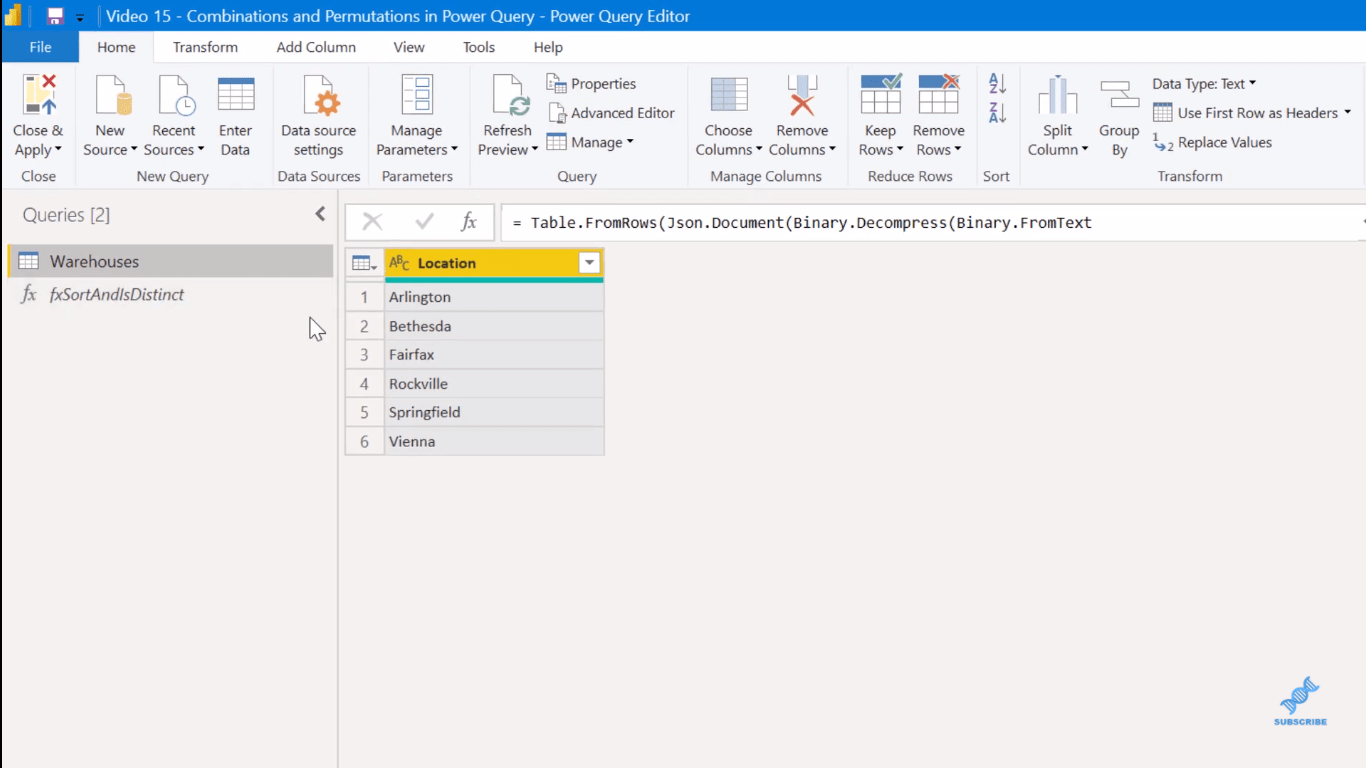
Och jag har utvecklat den här Power Query M-funktionen, som jag har använt för att bearbeta kombinationer och permutationer.

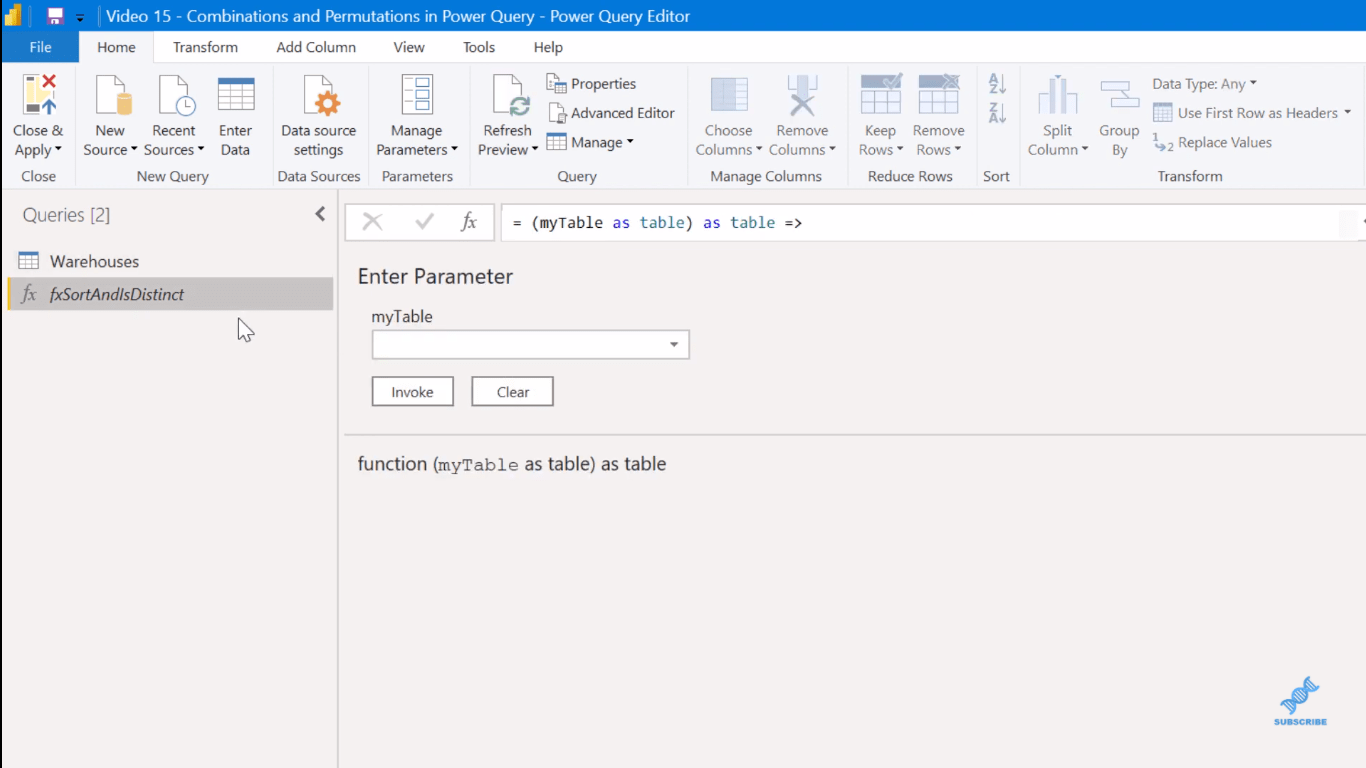
Först ska jag utveckla det första användningsfallet, som är permutationer med ersättning , det minst begränsande av gänget. Sättet att göra det i Power Query är att ta den här Warehouses- tabellen och referera till den (i DAX använder vi CROSSJOIN ).

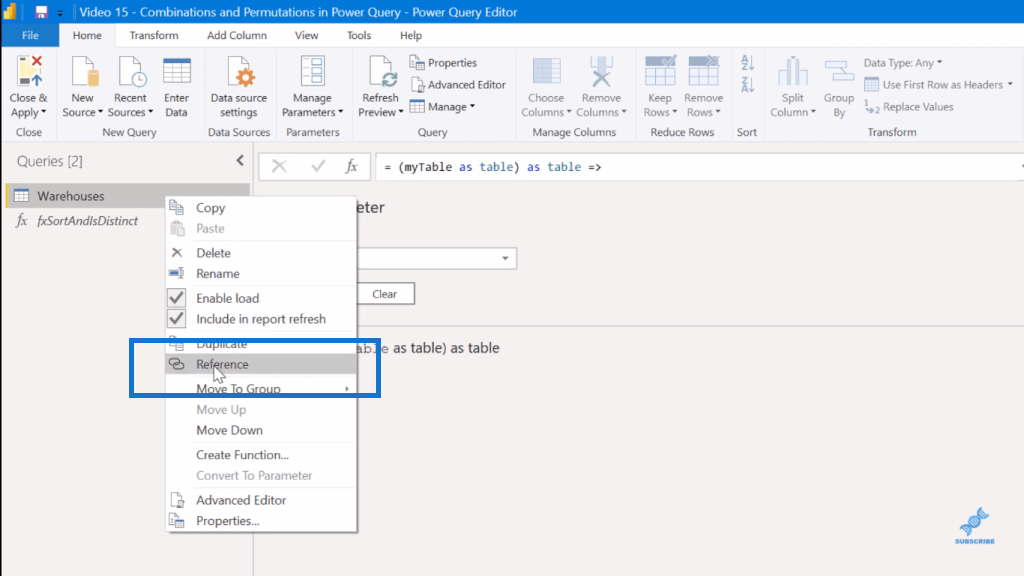
Jag kallar detta, Per w Rep (permutationer med ersättning).

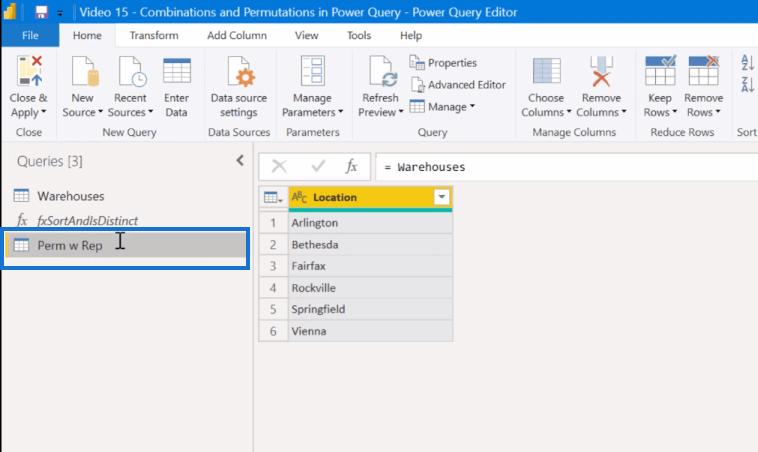
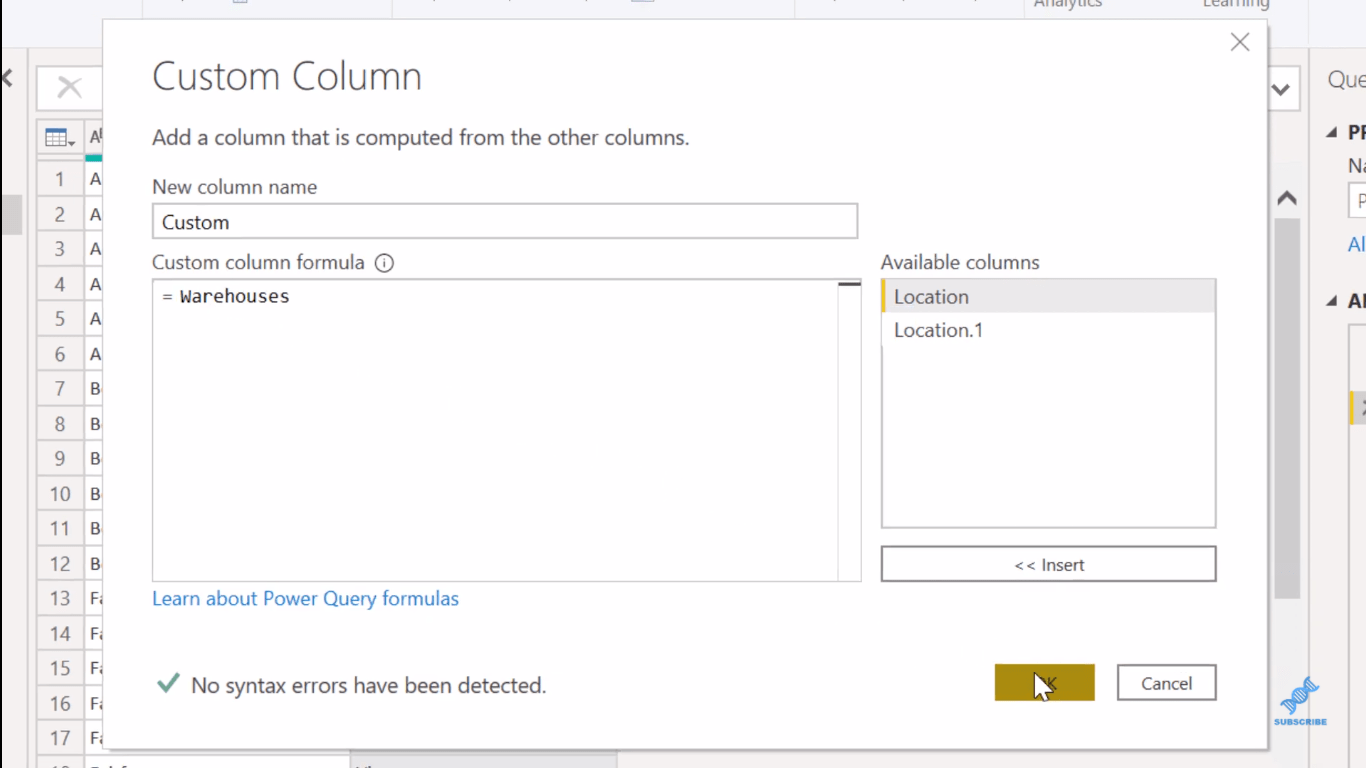
Det finns ett antal sätt du kan göra en korskoppling i Power Query. Det enklaste sättet jag har hittat är att bara gå till Lägg till kolumn och sedan Anpassad kolumn . I den anpassade kolumnformeln refererar du till tabellen Lager .

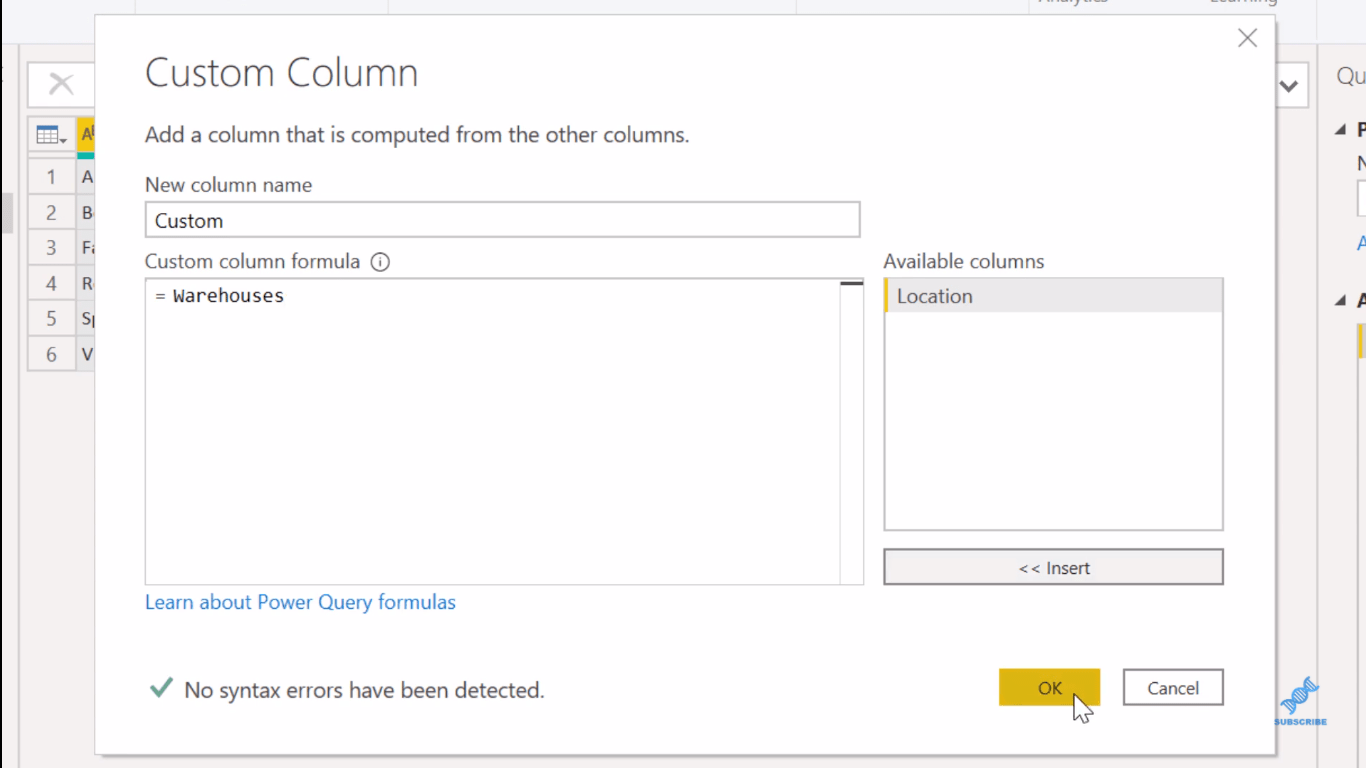
Och det vi hittar när vi klickar på OK är att det genererar en kapslad tabell.

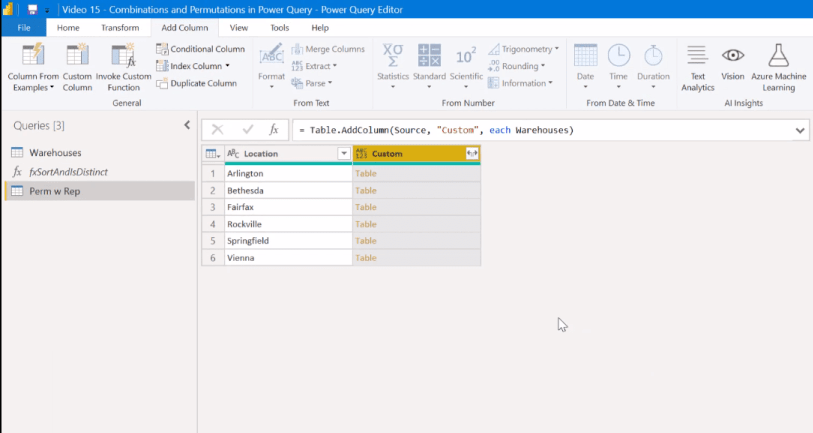
Sedan expanderar vi det och avklickar på Använd ursprungliga kolumnernamn som prefix .

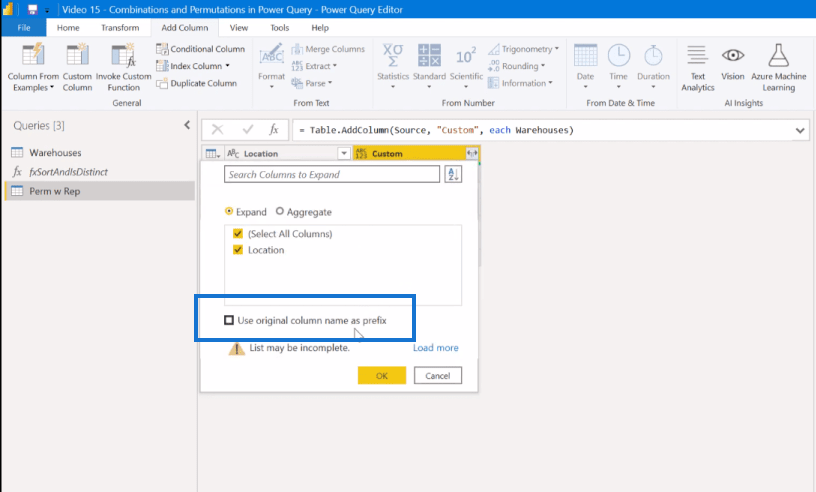
Och vi får denna Location.1 , som är alla möjliga kombinationer av två. Så det tar de första sex referenserna mot de andra sex kombinationerna. Den andra sexan gör samma sak hela vägen ner tills vi har 36 olika set.

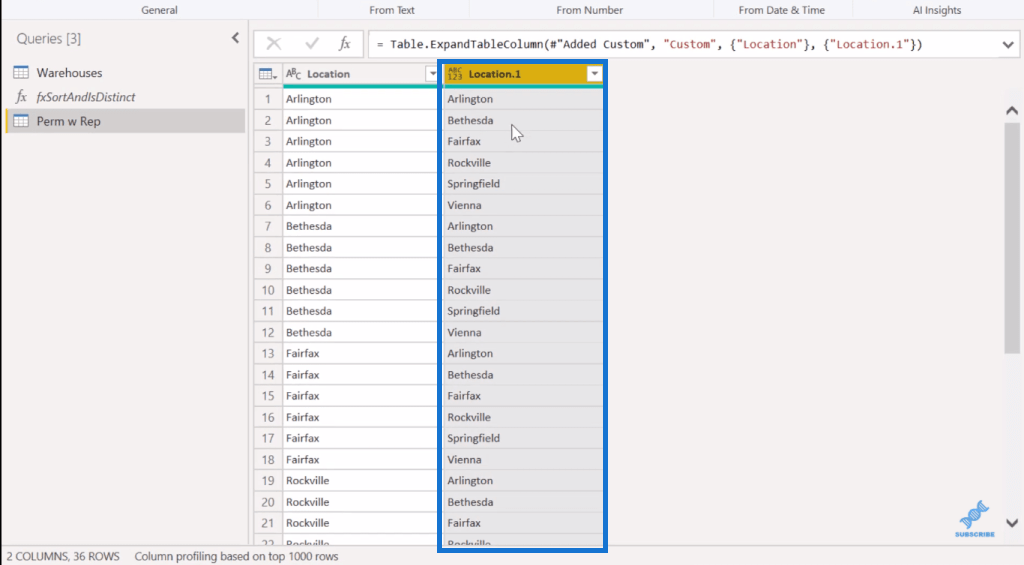
Vi kan göra den tredje genom att göra det här igen. Så vi går till Lägg till kolumn, sedan en anpassad kolumn och sedan Warehouses.

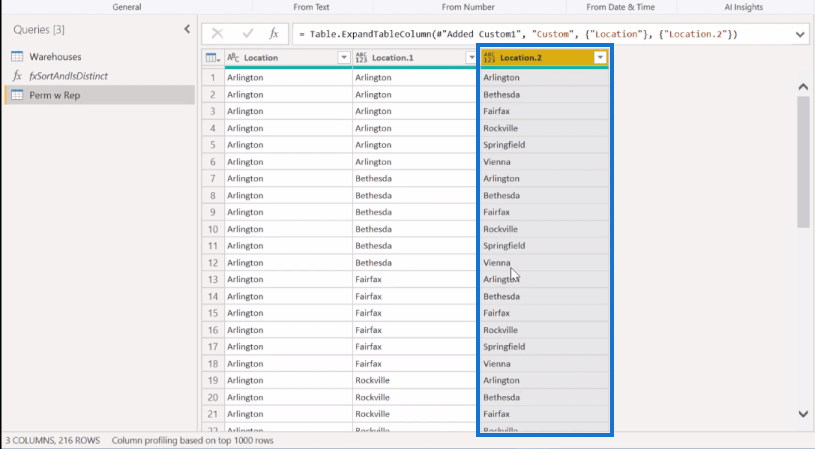
Och vi kommer att ha de 216 raderna som permutationer med ersättning.

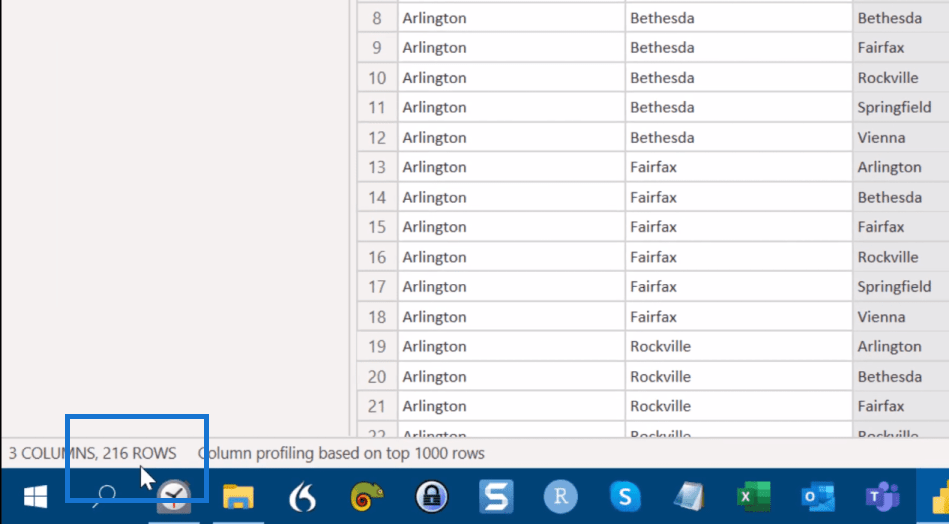
Och du kan se här nerifrån, 3 kolumner, 216 rader.

Nästa användningsfall är permutationer utan ersättning . Det vi tänker på här är i princip allt som har ett upprepat element. Så i den här tabellen kommer vi att titta på från rad 1 till rad 8.

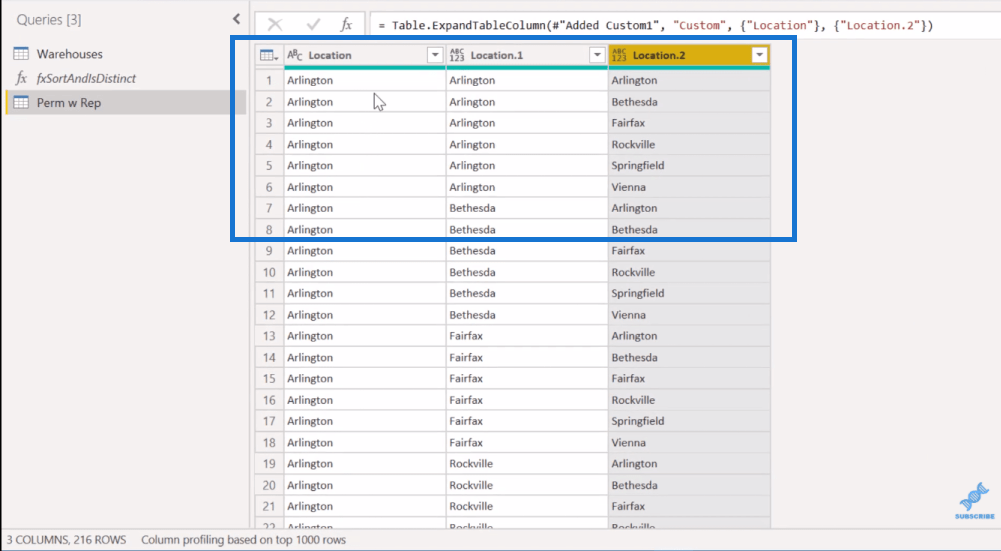
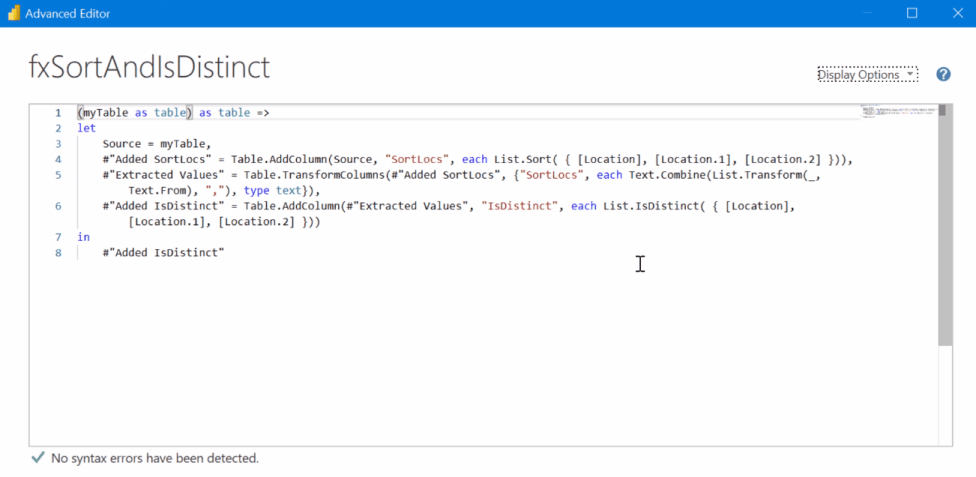
För att göra det tar vi en titt på den här funktionen, fxSortAndIsDistinct .

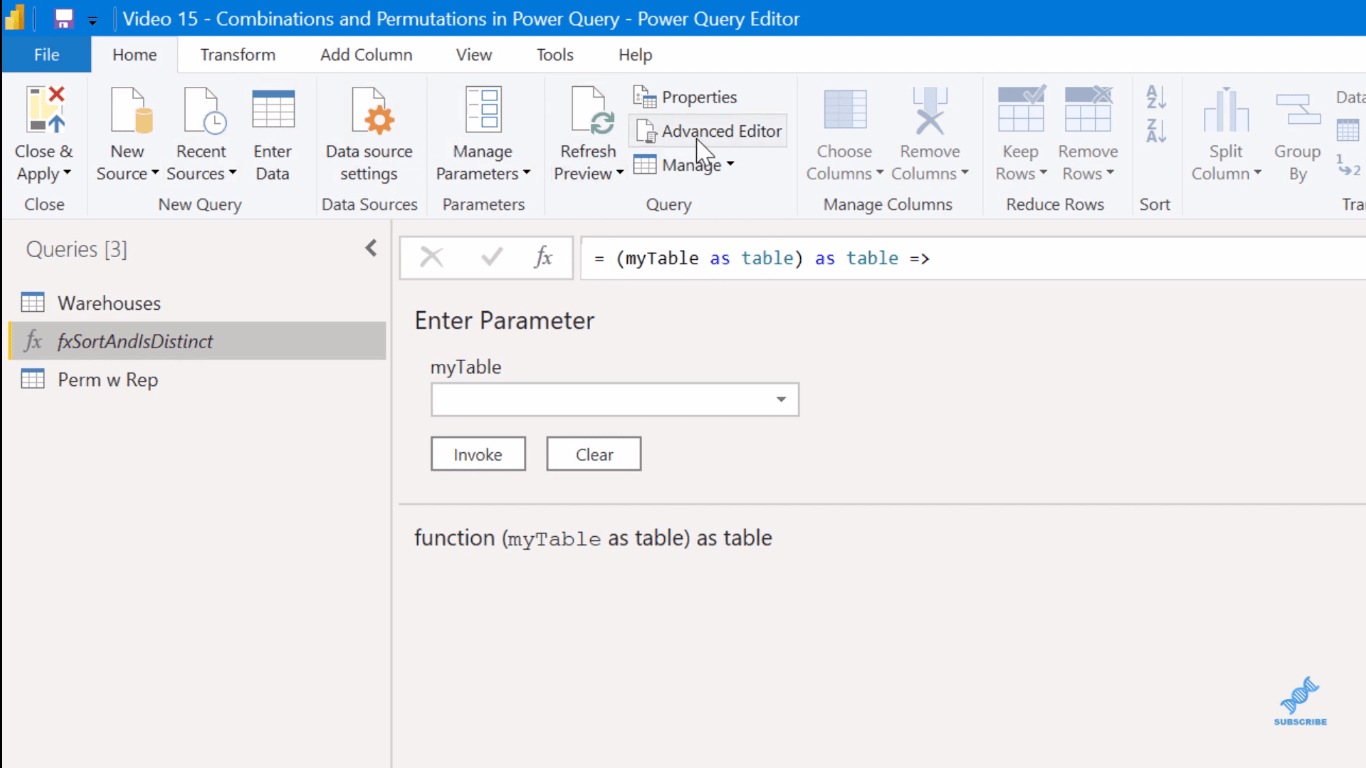
I Advanced Editor kan du se att detta i princip frågar efter en tabell, och sedan gör det en SortLocs . Men den viktiga delen här för "med ersättning" eller "utan ersättning" är att detta är en IsDistinct -funktion. Vad detta gör är bara att ta en lista med element och avgöra sant eller falskt, om det är distinkt eller om det har några dubbletter i listan med objekt.

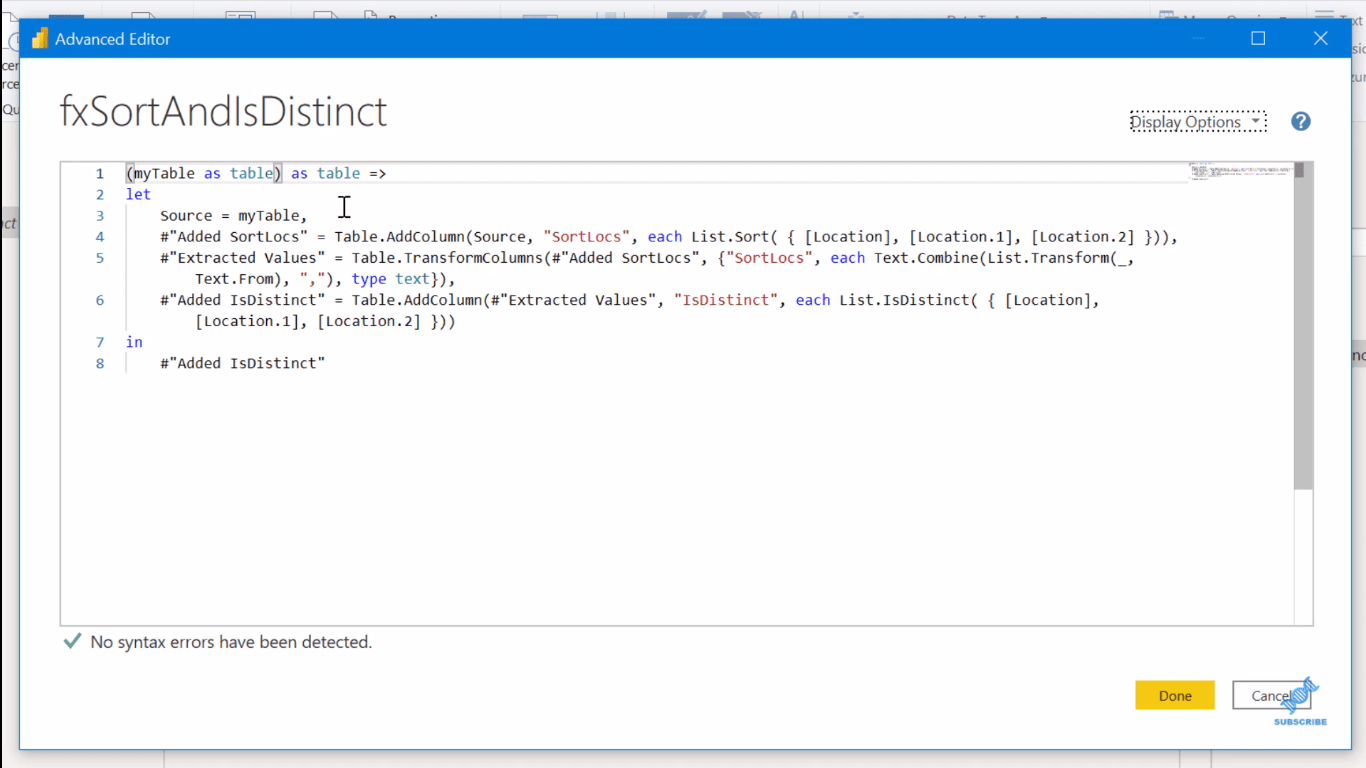
Så vi går hit, väljer Perm w Rep och trycker på Invoke .

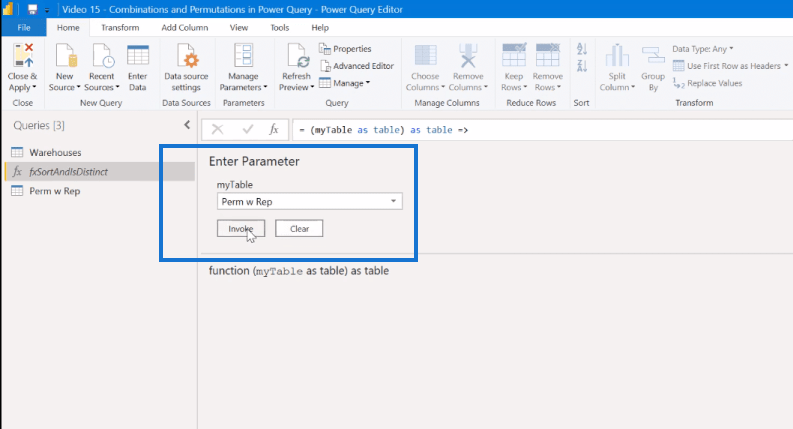
Detta kommer att ge oss dessa två nya kolumner, SortLocs och IsDistinct . Kom nu ihåg att de första åtta skivorna hade dubbletter och den nionde skivan var första gången vi såg den distinkta . Det är därför den nionde raden här är den första som visas som sann.

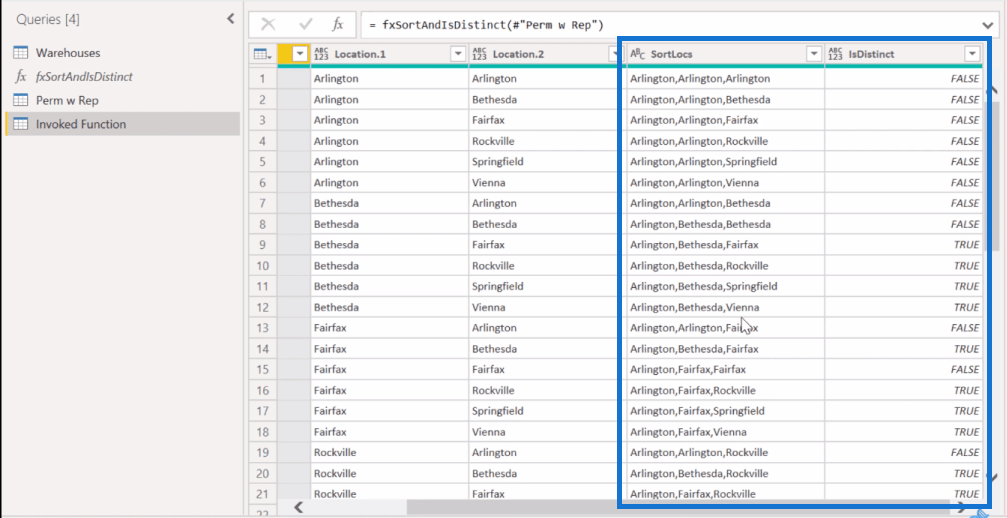
Om vi ​​tänker tillbaka på siffrorna som vi hade på faktorberäkningarna, förväntar vi oss 120 poster om vi tar ut de icke-särskiljande posterna. Så, låt oss försöka filtrera här och ta bort FALSK.

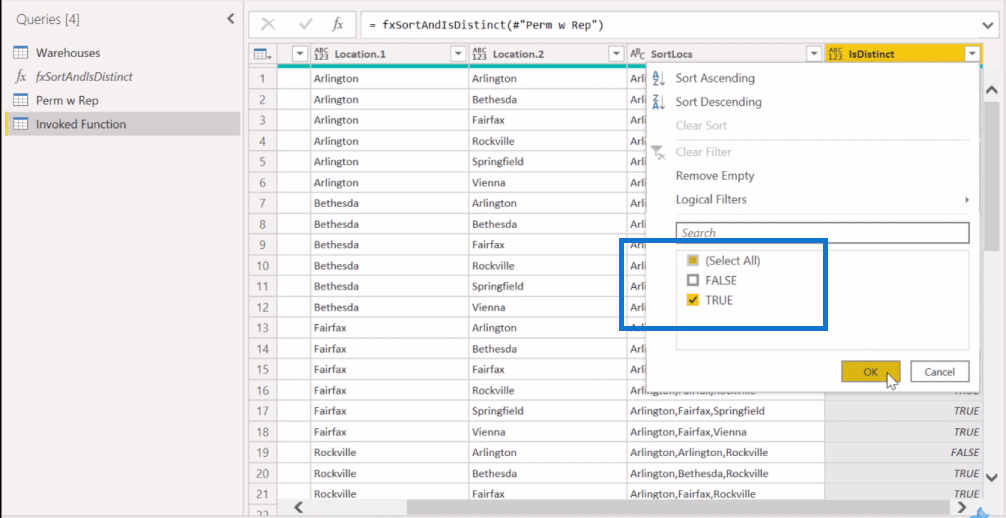
När vi gör det får vi här nere exakt de 120 rader som vi förväntar oss. Låt oss nu döpa om detta till Perm wo Rep (permutation utan ersättning).

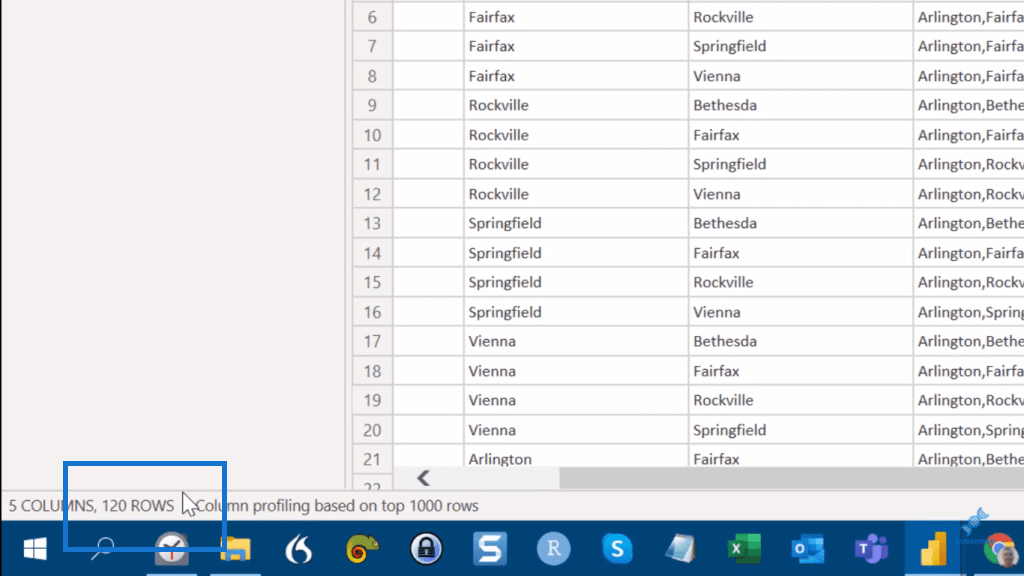
Kombinatorisk analys: Kombinationer i Power Query

Nu ska vi göra kombinationerna med ersättning . För att göra det gör vi helt enkelt processen igen och upprepar steget (anropad funktion). Så det är okej att vi har dubbletter, men vi vill inte ha uppsättningar som har samma element utan i en annan ordning.

I det här fallet, när vi pratar om kombinationer. Om du kommer ihåg att ABC är lika med BCA är lika med CAB, anses de alla vara dubbletter av varandra. Och sättet vi avgör det är genom sorteringsfunktionen ( fxSortAndIsDistinct ).

Om vi ​​går tillbaka till funktionen i Advanced Editor ser vi för den andra kolumnen att vi har tagit den listan och sorterat den alfabetiskt. Sedan extraherade vi värdena avgränsade med kommatecken från den listan. Nu har vi sorterat varje set i alfabetisk ordning. Vi har normaliserat ordningen för att göra det enkelt att hitta dubbletter.

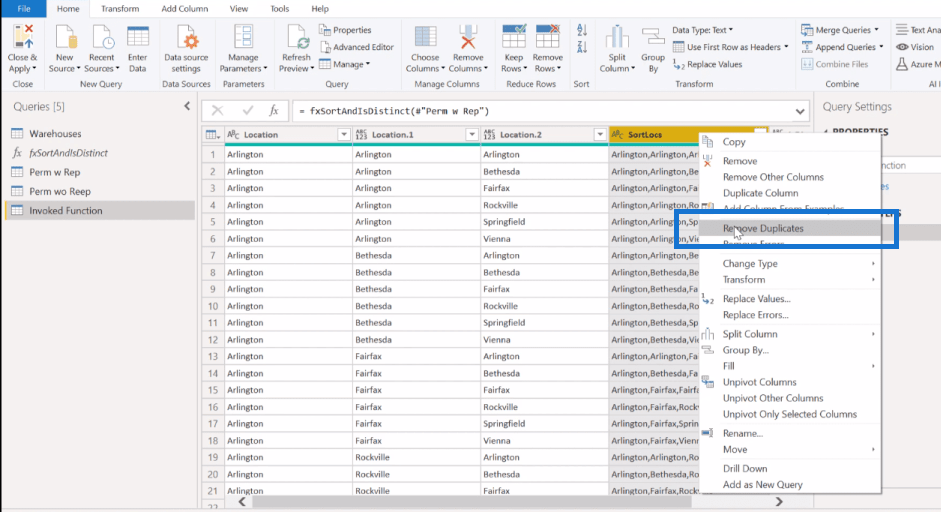
Om vi ​​nu går tillbaka till den här anropade funktionen, kom ihåg att vi letar efter 56 poster här. Så vi tar den här typen av plats ( SortLocs ) och tar bort våra dubbletter .

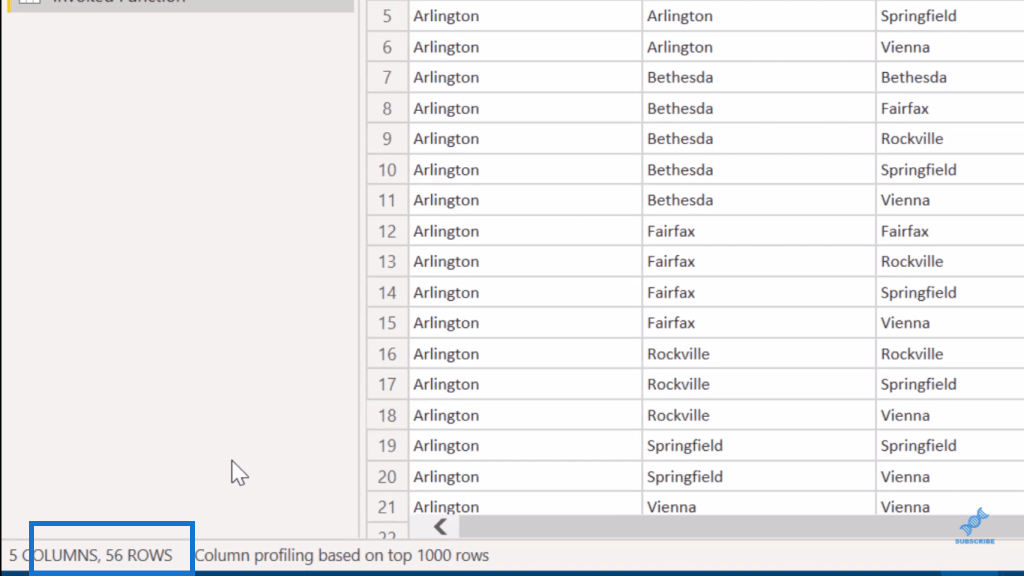
Med det får vi 56 rader.

Och så, detta är vårt tredje användningsfall. Låt oss döpa om detta till CC w Rep (kombinationer med ersättning).

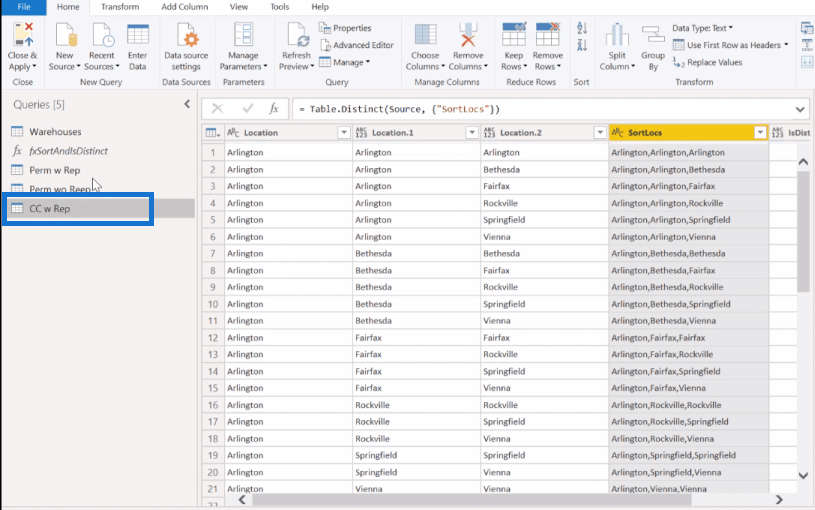
Låt oss avsluta detta genom att ta igen den där permutationstabellen med ersättningstabellen (Perm w Rep) och göra samma mönster (anropa). Sedan kommer vi att ta bort dubbletterna (SortLocs-kolumnen) eftersom detta är en kombination och ordningen spelar ingen roll. Den är utan ersättning, så vi vill också bara ha den distinkta listan . Så vi klickar av FALSE i IsDistinct-kolumnen.

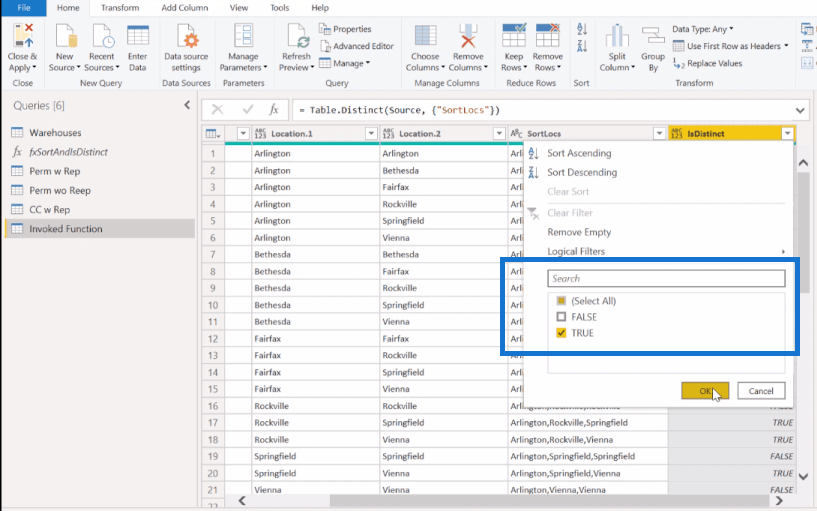
Med detta får vi 20 skivor. Och nu har vi alla våra fyra användningsfall.

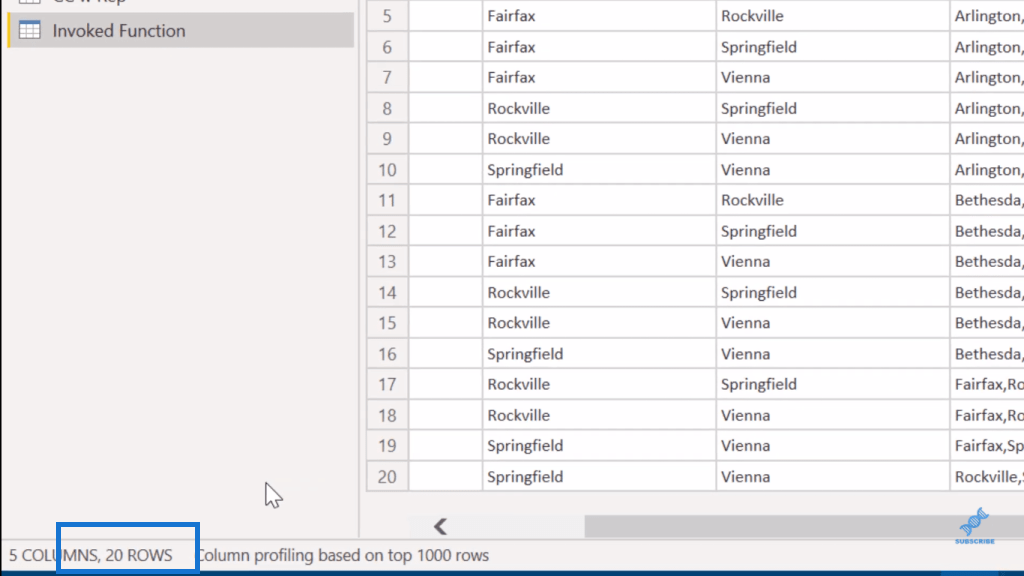
Slutsats

Så nu har vi alla våra fyra användningsfall. Du kan verkligen se hur kraftfullt detta är när det gäller att utveckla den där kombinatoriska analysen som ger dig kontroll över ersättning och distinkta element.

Detta är till och med tillämpligt i vissa mer komplexa fall där du har en partiell ersättning, eller kanske väljer ett duplicerat element för den första, men inte andra gången. Du kan fortfarande hantera det bra inombords.

Jag hoppas att du tyckte att det här var användbart. Kolla in länkarna nedan för mer innehåll. Du kan också se hela videon av denna handledning nedan.

Med vänliga hälsningar!