Skapa en datumtabell i LuckyTemplates
Ta reda på varför det är viktigt att ha en dedikerad datumtabell i LuckyTemplates och lär dig det snabbaste och mest effektiva sättet att göra det.
Om du har arbetat med Python för dataanalys eller maskininlärning har du troligen stött på NumPy-matriser. De är ett kraftfullt verktyg för att hantera numerisk data, men ibland måste data i dessa arrayer justeras eller "normaliseras" för att kunna användas effektivt i dina algoritmer. Men vad innebär det att normalisera en array?
För att normalisera en NumPy-matris måste du justera värdena i matrisen så att de hamnar inom ett visst intervall, vanligtvis mellan 0 och 1, eller så att de har en standardnormalfördelning med ett medelvärde på 0 och en standardavvikelse på 1 Detta görs ofta inom området maskininlärning och dataanalys för att säkerställa att alla inmatningsfunktioner har samma skala.

I den här artikeln kommer vi att utforska hur du kan normalisera en NumPy-array i Python. Vi kommer att titta på de olika metoderna du kan använda för att normalisera en NumPy-array och även titta på exempel som hjälper dig att bättre förstå konceptet.
Låt oss gå in i det!
Innehållsförteckning
Vad är grunderna för normalisering i Python?
Innan vi implementerar normalisering i Python måste du förstå vad normalisering innebär.

Därför kommer vi i det här avsnittet att gå över vad som är normalisering och dess kärnbegrepp.
Vad är normalisering?
Normalisering är en process som skalar och omvandlar data till ett standardiserat intervall. Detta görs genom att dividera varje element i data med en parameter. Parametern kan vara maxvärdet, intervallet eller någon annan norm.
Du kan normalisera NumPy-arrayen med den euklidiska normen (även känd som L2-normen). Dessutom kan du också normalisera NumPy-arrayer genom att skala om värdena mellan ett visst intervall, vanligtvis 0 till 1.
I Python tillhandahåller NumPy-biblioteket ett effektivt sätt att normalisera arrayer. Detta inkluderar också flerdimensionella arrayer och matriser.
Varför är normalisering viktigt?
Normalisering är viktigt eftersom det säkerställer att olika funktioner behandlas lika när man jämför och analyserar data. Du kan använda den för att eliminera potentiella fördomar eller avvikelser som kan uppstå på grund av varierande skalor.
Vad är normer?
Parametern som du använder för normalisering kan vara olika normer , till exempel den euklidiska normen (L2), Manhattan-normen (L1) eller maxnormen (L_inf). Du använder normer för att beräkna storleken på en vektor eller matris . Dessa används sedan som en skalningsfaktor för att normalisera data.
När vi arbetar med matriser använder vi ofta Frobenius-normen , som är en generalisering av den euklidiska normen för flerdimensionella arrayer.
Följande exempel visar normaliseringen av en matris med Frobenius-normen:
import numpy as np
# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
# Calculate the Frobenius norm
frobenius_norm = np.linalg.norm(matrix, 'fro')
# Normalize the matrix
normalized_matrix = matrix / frobenius_norm
print('Original Matrix:')
print(matrix)
print('nFrobenius Norm:')
print(frobenius_norm)
print('nNormalized Matrix:')
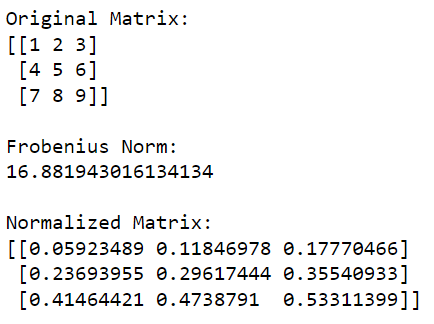
print(normalized_matrix)Denna Python-kod kommer först att importera NumPy-biblioteket och använda det för att skapa en matris. Den beräknar sedan Frobenius-normen för matrisen och delar sedan varje element i matrisen med detta värde för att normalisera det.
Utdata från denna kod ges nedan:
Vad är normalisering i maskininlärning?
Inom maskininlärning är normalisering ett viktigt förbearbetningssteg eftersom det förbättrar algoritmernas prestanda.
När du utför gradientbaserade optimeringstekniker kommer du att upptäcka att optimerade funktioner tenderar att konvergera snabbare och mer effektivt. Detta beror på att det minskar risken för dålig skalning eller försvinnande gradienter.
Vilka är normaliseringsteknikerna i Python?
Du kan utföra normalisering av arrayer på ett antal sätt. Vissa metoder är dock mer populära än andra på grund av deras höga effektivitet.
För det här avsnittet kommer vi att titta på de tre allmänt använda normaliseringsteknikerna:
Min-Max skalning
L1 Normalisering
L2 Normalisering
1. Hur man utför Min-Max-skalning
Min-max-skalning är också känd som linjär normalisering eller funktionsskalning. I min-max-skalning skalar vi värdena för en NumPy-matris så att de faller inom ett specificerat intervall, vanligtvis mellan 0 och 1.
För att göra detta subtraherar du minimivärdet från varje element och dividerar resultatet med skillnaden mellan högsta och lägsta värden.
Du kan representera min-max-skalningen matematiskt som:
x' = (x - min(x)) / (max(x) - min(x))Följande exempel visar hur du kan utföra min-max-skalning med NumPy-biblioteket:
import numpy as np
# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
# Perform min-max scaling
min_val = np.min(matrix)
max_val = np.max(matrix)
scaled_matrix = (matrix - min_val) / (max_val - min_val)
print('Original Matrix:')
print(matrix)
print('nMin-Max Scaled Matrix:')
print(scaled_matrix)Denna kod kommer först att importera NumPy och sedan beräkna minimi- och maxvärdena i matrisen, som den sedan skalar så att alla värden är mellan 0 (motsvarande det ursprungliga minimivärdet) och 1 (motsvarande det ursprungliga maxvärdet).
Utdata från denna kod ges nedan:

Min-max-skalning är en mycket vanlig form av skalning inom maskininlärning och dataförbearbetning.
2. Hur man utför L1-normalisering
L1-normaliseringen använder L1-normen, som är summan av de absoluta värdena för arrayelementen. Detta är särskilt användbart för glesa matriser. Det säkerställer att summan av de absoluta värdena för de normaliserade arrayelementen är lika med 1.
Formeln för L1-normalisering är:
x' = x / sum(|x|)Följande exempel visar hur du kan utföra L1-normalisering med NumPy:
import numpy as np
# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
# Perform L1 normalization
l1_norm = np.linalg.norm(matrix, 1, axis=1, keepdims=True)
l1_normalized_matrix = matrix / l1_norm
print('Original Matrix:')
print(matrix)
print('nL1 Normalized Matrix:')
print(l1_normalized_matrix)I denna kod beräknar np.linalg.norm (matris, 1, axel=1, keepdims=True) L1-normen för varje rad (detta görs genom att ange axel=1).
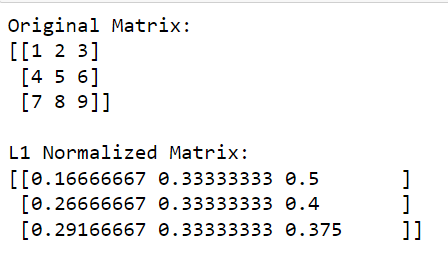
Denna operation returnerar en kolumnvektor där varje element är L1-normen för motsvarande rad. Genom att dividera den ursprungliga matrisen med dessa normer (genom att utföra divisionen elementmässigt) får vi den L1-normaliserade versionen av matrisen.
Utgången ges nedan:
3. Hur man utför L2-normalisering
L2-normalisering använder L2-normen, som är kvadratroten av summan av de kvadratiska matriselementen.
Denna metod omvandlar den normaliserade matrisen till en enhetsvektor med en 2-norm på 1. L2-normalisering är användbar för dimensionsreduktion och säkerställer lika betydelse för alla funktioner.
Formeln för L2-normalisering är:
x' = x / sqrt(sum(x^2))Så här kan du utföra L2-normalisering med NumPy :
import numpy as np
# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
# Perform L2 normalization
l2_norm = np.linalg.norm(matrix, 2, axis=1, keepdims=True)
l2_normalized_matrix = matrix / l2_norm
print('Original Matrix:')
print(matrix)
print('nL2 Normalized Matrix:')
print(l2_normalized_matrix)I den här koden beräknar np.linalg.norm(matrix, 2, axis=1, keepdims=True) L2-normen (euklidisk norm) för varje rad (detta görs genom att ange axis=1). Denna operation returnerar en kolumnvektor där varje element är L2-normen för motsvarande rad.
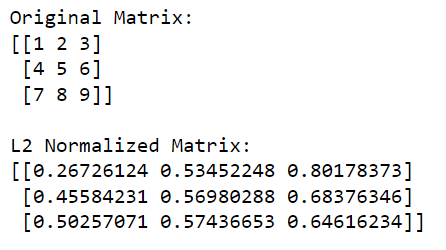
Genom att dividera den ursprungliga matrisen med dessa normer (genom att utföra divisionen elementmässigt) får vi den L2-normaliserade versionen av matrisen.
Utgången ges nedan:
Okej, nu när vi har gått igenom de populära sätten att skapa en normaliserad array med NumPy, låt oss ta en titt på hur du kan göra samma sak med andra Python-bibliotek i nästa avsnitt.
Hur man använder Scikit-Learn för normalisering i Python
Scikit-learn är ett kraftfullt Python-bibliotek för maskininlärning. Den tillhandahåller flera verktyg för förbearbetning av data.
Ett verktyg du kan använda är modulen sklearn.preprocessing , som erbjuder olika tekniker för att utföra normalisering. Det finns många olika skalningsfunktioner, transformatorer och normalisatorer tillgängliga. Vi kommer dock att fokusera på MinMaxScaler och normalisera .
För att förbehandla data med scikit-learn använder du främst transformatorns API. Detta inkluderar metoderna fit , transform och fit_transform .
1. Hur man normaliserar array med MinMaxScaler
MinMaxScaler är en skalare som normaliserar data till ett specificerat intervall, vanligtvis [0, 1] .
Formeln för MinMaxScalar ges nedan:
scaled_value = (value - min_value) / (max_value - min_value)För att implementera MinMaxScaler kan du följa dessa steg:
Importera de nödvändiga biblioteken:
import numpy as np
from sklearn.preprocessing import MinMaxScalerSkapa en NumPy-array:
data = np.array([[1., 2., 5.], [3., 6., 8.], [5., 10., 12.]])Instantiera MinMaxScaler och anpassa den till data:
scaler = MinMaxScaler()
scaler.fit(data)Transformera data med metoden transform eller fit_transform :
normalized_data = scaler.transform(data)Utdata från denna kod ges nedan:

Som du kan se i utgången har MinMaxScalarMatrix endast värden från 0 till 1.
2. Hur man utför normalisering av rader på plats
Du kan också använda normaliseringen av raderna på plats som ett alternativ genom att använda normaliseringsfunktionen .
Denna metod normaliserar varje inmatningsmatris eller funktion oberoende genom att skala vektorn till en enhetsnorm. Som standard använder normaliseringsfunktionen L2-normen för att utföra enkel normalisering, men du kan välja andra normalternativ.
Följande exempel visar normalisering av rader på plats:
from sklearn.preprocessing import normalize
import numpy as np
# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]], dtype=float)
# Apply in-place row normalization
normalize(matrix, norm='l2', copy=False)
print('L2 Normalized Matrix:')
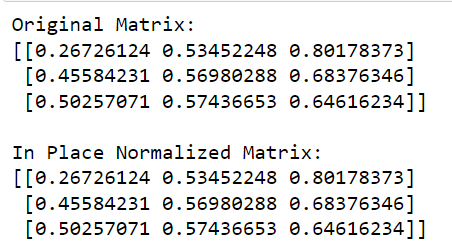
print(matrix)I den här koden anropar vi normaliseringsfunktionen från sklearn , definierar normen som ska användas ('l2' i det här fallet) och ställer in copy=False för att utföra normalisering på plats.
Utdata från denna kod ges nedan:
Om du vill veta mer om maskininlärning i , kolla in följande video:
Slutgiltiga tankar
När du utforskar datavetenskap och maskininlärning ytterligare kommer du att upptäcka att normaliseringsprocessen är ett viktigt steg i din pipeline för förbearbetning av data.
För det första placerar det olika egenskaper på en gemensam skala. Detta gör dina modeller mindre känsliga för omfattningen av input. Det kan avsevärt förbättra prestandan för många maskininlärningsalgoritmer.
För det andra hjälper det dig att påskynda träningsprocessen. Vissa algoritmer, särskilt de som baseras på beräknade avståndsberäkningar, konvergerar snabbare när data normaliseras.
Genom att lära dig att normalisera data, utrustar du dig själv med en avgörande färdighet. Normalisering är ett praktiskt verktyg som används rutinmässigt i verkliga tillämpningar. Det hjälper dig att minska sannolikheten för oväntade resultat på grund av extremvärden eller skillnader i enheter.
Som alla verktyg ligger nyckeln till att bemästra normalisering i praktiken. Så tveka inte att smutsa ner händerna och experimentera med olika datauppsättningar och slumpmässiga värden. Världen av är ditt ostron. Glad kodning!
Ta reda på varför det är viktigt att ha en dedikerad datumtabell i LuckyTemplates och lär dig det snabbaste och mest effektiva sättet att göra det.
Denna korta handledning belyser LuckyTemplates mobilrapporteringsfunktion. Jag ska visa dig hur du kan utveckla rapporter effektivt för mobila enheter.
I denna LuckyTemplates Showcase går vi igenom rapporter som visar professionell serviceanalys från ett företag som har flera kontrakt och kundengagemang.
Gå igenom de viktigaste uppdateringarna för Power Apps och Power Automate och deras fördelar och konsekvenser för Microsoft Power Platform.
Upptäck några vanliga SQL-funktioner som vi kan använda som sträng, datum och några avancerade funktioner för att bearbeta eller manipulera data.
I den här handledningen kommer du att lära dig hur du skapar din perfekta LuckyTemplates-mall som är konfigurerad efter dina behov och preferenser.
I den här bloggen kommer vi att visa hur man lager fältparametrar med små multiplar för att skapa otroligt användbara insikter och bilder.
I den här bloggen kommer du att lära dig hur du använder LuckyTemplates ranknings- och anpassade grupperingsfunktioner för att segmentera en exempeldata och rangordna den enligt kriterier.
I den här handledningen kommer jag att täcka en specifik teknik kring hur man visar Kumulativ total endast upp till ett specifikt datum i dina bilder i LuckyTemplates.
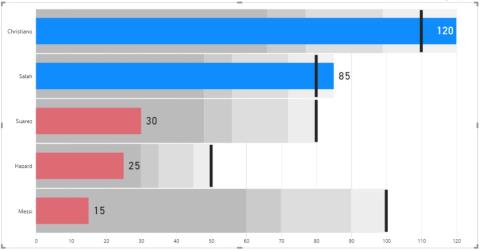
Lär dig hur du skapar och anpassar punktdiagram i LuckyTemplates, som huvudsakligen används för att mäta prestanda mot mål eller tidigare år.