Ako zmeniť pozadie v PowerPointe 2019
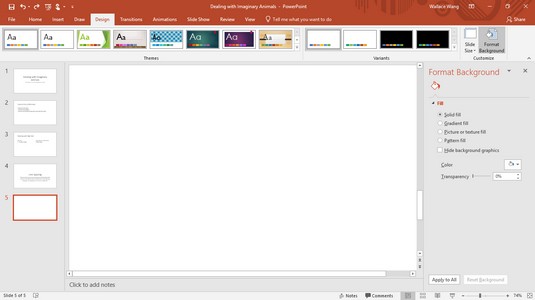
Naučte sa, ako jednoducho zmeniť pozadie v PowerPointe 2019, aby vaše prezentácie pôsobili pútavo a profesionálne. Získajte tipy na plnú farbu, prechod, obrázky a vzory.
Ako viete, či je predpovedaný trend skutočný? Ak vidíte základnú líniu, ktorá vyzerá, že sa posúva nahor alebo nadol, predstavuje to skutočný trend alebo je to len náhodná odchýlka? Ak chcete odpovedať na tieto otázky, musíte sa dostať do pravdepodobnosti a štatistiky. Našťastie sa do nich nemusíte dostať príliš ďaleko – možno až po zápästie.
Základný myšlienkový pochod vyzerá takto:
Pomocou Excelu zistíte, aká je korelácia medzi príjmami z predaja a súvisiacimi časovými obdobiami.
Nezáleží na tom, či uvádzam toto obdobie ako január 2011, február 2011, marec 2011 . . . decembra 2016, alebo ako 1., 2., 3. . . 72.
Ak medzi výnosmi a časovým obdobím neexistuje žiadny vzťah, meraný koreláciou, neexistuje žiadny trend a nemusíte sa o to starať.
V prípade, že je vzťah medzi príjmami a časových období, budete musieť vybrať najlepší spôsob, ako zvládnuť tento trend.
Potom, čo Excel vypočíta koreláciu, musíte sa rozhodnúť, či predstavuje skutočný vzťah medzi časovým obdobím a sumou výnosov, alebo či je to len šťastný pokus.
Ak je pravdepodobnosť, že je to len šťastie, menšia ako 5 percent, ide o skutočný trend. (Na 5 percentách tiež nie je nič magické – je to bežné. Niektorí ľudia uprednostňujú použitie 1 percenta ako svoje kritérium – je to konzervatívnejšie ako 5 percent a cítia sa o niečo bezpečnejšie.) To vyvoláva problém štatistickej významnosti: Aká úroveň pravdepodobnosti vyžadujete predtým, než sa rozhodnete, že niečo (tu, korelácia) je skutočný McCoy?
Existujú rôzne metódy na testovanie štatistickej významnosti korelačného koeficientu. Tu sú tri populárne metódy:
Existujú aj iné populárne metódy na testovanie štatistickej významnosti korelačného koeficientu. Každý vráti trochu iný výsledok. V praxi sa takmer vždy rozhodnete rovnako (korelácia je alebo nie je výrazne odlišná od nuly), bez ohľadu na metódu, ktorú si vyberiete.
Ak dospejete k záveru, že trend korelačných meraní je skutočný (a keď je pravdepodobnosť menšia ako 1 percento, že korelácia je duch, pravdepodobne by ste mali prijať tento záver), musíte si položiť ďalšie dve otázky:
Ak príjmy konkurencie klesajú ako vaše (alebo ak obe skupiny príjmov rastú), zistíte pravdepodobnú významnú koreláciu medzi vašimi príjmami a príjmami konkurencie. Ale je celkom možné – dokonca pravdepodobné – že medzi ich a vašimi príjmami neexistuje žiadny skutočný, príčinný vzťah. Môže sa stať, že váš aj ich korelujú so skutočným kauzálnym faktorom: Veľkosť celkového trhu sa mení. V takom prípade by pre vás bolo pravdepodobne oveľa lepšie použiť ako predikčnú premennú mieru celkovej veľkosti trhu. V tomto scenári má veľkosť trhu priamy, príčinný vzťah k vašim príjmom, zatiaľ čo príjmy vašej konkurencie majú k vašim príjmom iba nepriamy vzťah.
Spôsob, ako zvládnuť tento druh situácie, je najprv odstrániť trend oboch premenných pomocou transformácie.
Alebo môžete radšej vytvoriť svoju prognózu pomocou prístupu, ktorý nemusí nevyhnutne dobre zvládnuť trendy, ako sú kĺzavé priemery alebo jednoduché exponenciálne vyhladzovanie. Jedným z dôvodov je to, že možno zistíte, že regresný prístup s vaším súborom údajov nie je taký presný prognostik ako kĺzavé priemery alebo vyhladzovanie. Znova skontrolujte, či môžete transformovať údaje na odstránenie trendu.
Naučte sa, ako jednoducho zmeniť pozadie v PowerPointe 2019, aby vaše prezentácie pôsobili pútavo a profesionálne. Získajte tipy na plnú farbu, prechod, obrázky a vzory.
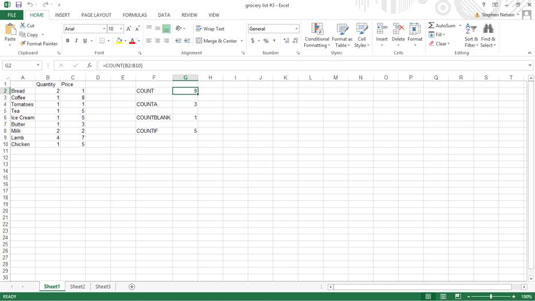
Excel poskytuje štyri užitočné štatistické funkcie na počítanie buniek v hárku alebo zozname: COUNT, COUNTA, COUNTBLANK a COUNTIF. Pre viac informácií o Excel funkciách, pokračujte.
Objavte efektívne klávesové skratky v Exceli 2013 pre zobrazenie, ktoré vám pomôžu zlepšiť produktivitu. Všetky skratky sú začiatkom s Alt+W.
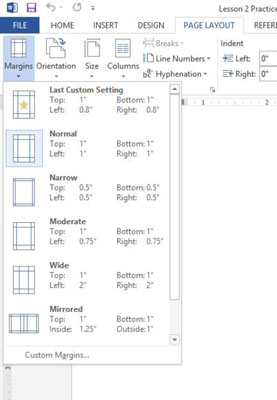
Naučte sa, ako nastaviť okraje v programe Word 2013 s naším jednoduchým sprievodcom. Tento článok obsahuje užitočné tipy a predvoľby okrajov pre váš projekt.
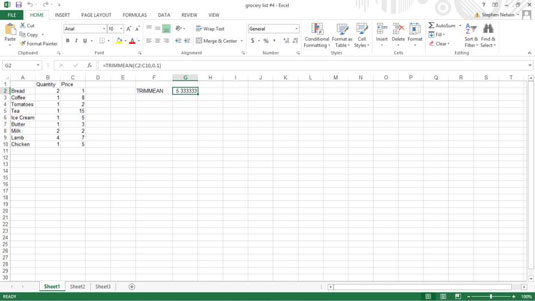
Excel vám poskytuje niekoľko štatistických funkcií na výpočet priemerov, režimov a mediánov. Pozrite si podrobnosti a príklady ich použitia.
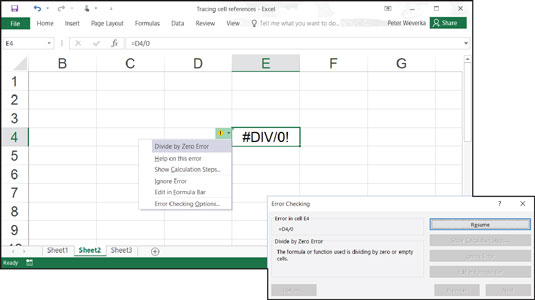
Excel 2016 ponúka niekoľko efektívnych spôsobov, ako opraviť chyby vo vzorcoch. Opravy môžete vykonávať po jednom, spustiť kontrolu chýb a sledovať odkazy na bunky.
V niektorých prípadoch Outlook ukladá e-mailové správy, úlohy a plánované činnosti staršie ako šesť mesiacov do priečinka Archív – špeciálneho priečinka pre zastarané položky. Učte sa, ako efektívne archivovať vaše položky v Outlooku.
Word vám umožňuje robiť rôzne zábavné veci s tabuľkami. Učte sa o vytváraní a formátovaní tabuliek vo Worde 2019. Tabuľky sú skvelé na organizáciu informácií.
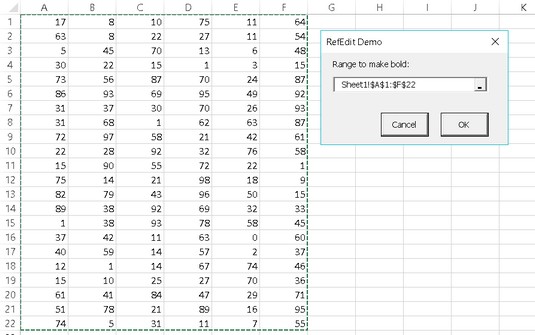
V článku sa dozviete, ako umožniť používateľovi vybrať rozsah v Excel VBA pomocou dialógového okna. Získajte praktické tipy a príklady na zlepšenie práce s rozsahom Excel VBA.
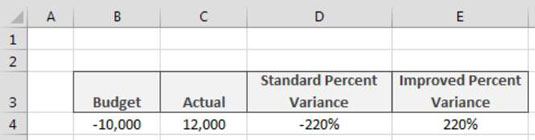
Vzorec na výpočet percentuálnej odchýlky v Exceli s funkciou ABS pre správne výsledky aj so zápornými hodnotami.