Ako zmeniť pozadie v PowerPointe 2019
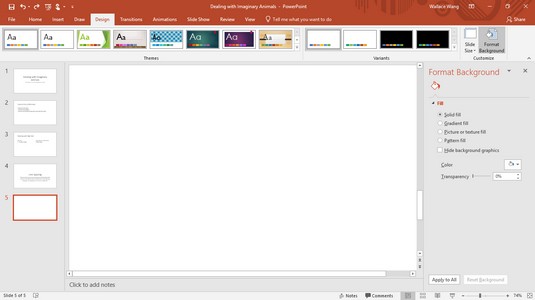
Naučte sa, ako jednoducho zmeniť pozadie v PowerPointe 2019, aby vaše prezentácie pôsobili pútavo a profesionálne. Získajte tipy na plnú farbu, prechod, obrázky a vzory.
V Exceli vám binomické rozdelenia umožňujú vypočítať pravdepodobnosti v dvoch situáciách. Okrem toho by ste mali poznať jedinú funkciu hypergeometrického rozdelenia, pretože súvisí s binomickými funkciami. Binomické distribúcie by ste použili v týchto situáciách:
Keď máte obmedzený počet nezávislých pokusov alebo testov, ktoré môžu byť úspešné alebo neúspešné
Keď je úspech alebo neúspech ktoréhokoľvek pokusu nezávislý od ostatných pokusov
Funkcia BINOM.DIST nájde pravdepodobnosť binomického rozdelenia. Funkcia používa syntax
=BINOM.DIST(čísla, pokusy, pravdepodobnosti, kumulatívne)
kde číslo_s je určený počet požadovaných úspechov, počet pokusov sa rovná počtu pokusov, na ktoré sa pozriete, pravdepodobnosť_s sa rovná pravdepodobnosti úspechu v pokuse a kumulatívny je prepínač, ktorý je nastavený buď na logickú hodnotu TRUE (ak chcete vypočítať kumulatívnu pravdepodobnosť) alebo logickú hodnotu FALSE (ak chcete vypočítať presnú pravdepodobnosť).
Napríklad, ak vydavateľ chce poznať pravdepodobnosť vydania troch najpredávanejších kníh zo súboru desiatich kníh, pričom pravdepodobnosť vydania najpredávanejšej knihy je desať percent, vzorec je
=BINOM.DIST(3;10;.1;FALSE)
ktorý vráti hodnotu . To naznačuje, že existuje zhruba 6-percentná šanca, že v súbore desiatich kníh vydavateľ vydá presne tri najpredávanejšie knihy.
Na výpočet pravdepodobnosti, že vydavateľ vydá jeden, dva alebo tri bestsellery v súbore desiatich kníh, je vzorec
=BINOM.DIST(3;10;.1;TRUE)
ktorý vráti hodnotu , čo naznačuje, že existuje zhruba 99-percentná šanca, že vydavateľ vydá jeden až tri bestsellery v súbore desiatich kníh.
Funkcie BINOM.INV nájdu najmenšiu hodnotu, pre ktorú sa kumulatívne binomické rozdelenie rovná alebo prekračuje zadané kritérium alebo hodnotu alfa. Funkcia používa syntax
=BINOM.INV(skúšky,pravdepodobnosť_s,alfa)
kde počet pokusov sa rovná počtu Bernoulliho pokusov, na ktoré sa pozriete, pravdepodobnosť_s sa rovná pravdepodobnosti úspechu v pokuse a alfa sa rovná hodnote kritéria, ktoré chcete splniť alebo prekonať.
Ak nastavíte pokusy na 10, pravdepodobnosť na 0,5 a hodnotu kritéria napríklad na 0,75, vzorec je
=BINOM.INV(10;0,5;0,75)
čo vráti hodnotu 6.
Funkcia BINOM.DIST.RANGE nájde pravdepodobnosť výsledku pokusu alebo rozsah výsledkov pokusu pre binomické rozdelenie. Funkcia používa syntax
=BINOM.DIST.RANGE(pokusy,pravdepodobnosti,čísla,[čísla2])
kde počet pokusov sa rovná počtu pokusov, na ktoré sa pozriete, pravdepodobnosť_s sa rovná pravdepodobnosti úspechu v pokuse, číslo_s nastaví počet úspešných pokusov a číslo_s2 (čo je voliteľný argument) nastaví maximálny počet úspešných pokusov.
Ak nastavíte pokusy na 10, pravdepodobnosť na 0,5 a počet úspešných pokusov na 3, napríklad, vzorec je
=BINOM.DIST.RANGE(10;0,5;3)
čo vráti hodnotu 0,11718, čo znamená, že pravdepodobnosť presne troch úspešných pokusov sa rovná približne 12 %.
Ak nastavíte pokusy na 10, pravdepodobnosť na 0,5 a počet úspešných pokusov na čokoľvek od 3 do 10, napríklad vzorec je
=BINOM.DIST.RANGE(10;0,5;3;10)
ktorá vráti hodnotu , čo znamená, že pravdepodobnosť počtu úspešných pokusov sa pohybuje v rozmedzí od 3 do 10, ktorá sa rovná približne 95 %.
Funkcia NEGBINOM.DIST na základe konštanty pravdepodobnosti úspechu nájde pravdepodobnosť, že pred stanoveným počtom úspechov dôjde k zadanému počtu zlyhaní. Funkcia používa syntax
=NEGBINOM.DIST(číslo_f,číslo_s,pravdepodobnosť_s)
kde číslo_f je zadaný počet zlyhaní, číslo_s je zadaný počet úspechov, pravdepodobnosť_s je pravdepodobnosť úspechu a kumulatívna je prepínač, ktorý nastavíte na 0 alebo FALSE, ak chcete kumulatívne rozdelenie a na 1 alebo TRUE, ak chcete rozdelenia pravdepodobnosti.
Predpokladajme napríklad, že ste ropným operátorom divokej mačky a chcete vedieť, aká je šanca, že sa vám nepodarí nájsť ropu presne v desiatich vrtoch, kým nenájdete ropu presne v jednom vrte. Ak je šanca na úspech 5 percent, môžete nájsť šancu, že pred vŕtaním a hľadaním ropy desaťkrát zlyháte, pomocou vzorca
=NEGBINOM.DIST(10;2;.05;0)
ktorá vráti hodnotu 0,016465266, čo znamená, že je menej ako 2-percentná šanca, že desaťkrát zlyháte, kým narazíte na gejzír.
Funkcia CRITBINOM, ktorá je skutočne starou funkciou Excelu a je dostupná v najnovších verziách Excelu z dôvodov spätnej kompatibility, nájde najmenšiu hodnotu, pre ktorú sa kumulatívne binomické rozdelenie rovná alebo prekračuje hodnotu kritéria. Funkcia používa syntax
=CRITBINOM(skúšky,pravdepodobnosť_s,alfa)
kde pokusy je počet Bernoulliho pokusov, pravdepodobnosť_s je pravdepodobnosť úspechu každého pokusu a alfa sa rovná hodnote vášho kritéria. Obaja probability_s a alfa argumenty sa musí pohybovať medzi 0 a 1.
Funkcia HYPERGEOMETRIC vracia pravdepodobnosť zadaného počtu vzorových úspechov. Hypergeometrické rozdelenie sa podobá binomickému rozdeleniu, až na nepatrný rozdiel. V hypergeometrickom rozložení úspech v jednom pokuse ovplyvňuje úspech v inom pokuse. Funkciu HYPGEOM.DIST zvyčajne používate, keď odoberáte vzorky z konečnej populácie a nenahrádzate vzorky pre následné pokusy. Funkcia používa syntax
=HYPGEOM.DIST(vzorky, cislo_vzorky, populacie_, cislo_pop, kumulativne)
kde sample_s sa rovná určenému počtu úspechov vo vzorke, number_sample udáva veľkosť vzorky, populácia_s udáva počet úspechov v populácii, number_pop udáva veľkosť populácie a kumulatívne je prepínač, ktorý Excelu povie, aby vrátil buď kumulatívne rozdelenie. (indikované hodnotou argumentu 1 alebo TRUE) alebo hustotou pravdepodobnosti (indikované hodnotou argumentu 0 alebo FALSE).
Ako príklad hypergeometrickej distribúcie predpokladajme, že chcete vypočítať pravdepodobnosť, že na vzorke 30 položiek bude 5 úspešných. Ďalej predpokladajme, že viete, že v rámci populácie 4 000 položiek je 1 000 úspešných. Na tento výpočet použijete nasledujúci vzorec:
=HYPGEOM.DIST(5;30;1000;4000;0)
ktorá vráti hodnotu 0,0104596, čo znamená, že šanca, že práve 5 položiek bude úspešných v súbore 30 položiek vzhľadom na charakteristiky populácie, sa rovná približne 10 percentám.
Naučte sa, ako jednoducho zmeniť pozadie v PowerPointe 2019, aby vaše prezentácie pôsobili pútavo a profesionálne. Získajte tipy na plnú farbu, prechod, obrázky a vzory.
Excel poskytuje štyri užitočné štatistické funkcie na počítanie buniek v hárku alebo zozname: COUNT, COUNTA, COUNTBLANK a COUNTIF. Pre viac informácií o Excel funkciách, pokračujte.
Objavte efektívne klávesové skratky v Exceli 2013 pre zobrazenie, ktoré vám pomôžu zlepšiť produktivitu. Všetky skratky sú začiatkom s Alt+W.
Naučte sa, ako nastaviť okraje v programe Word 2013 s naším jednoduchým sprievodcom. Tento článok obsahuje užitočné tipy a predvoľby okrajov pre váš projekt.
Excel vám poskytuje niekoľko štatistických funkcií na výpočet priemerov, režimov a mediánov. Pozrite si podrobnosti a príklady ich použitia.
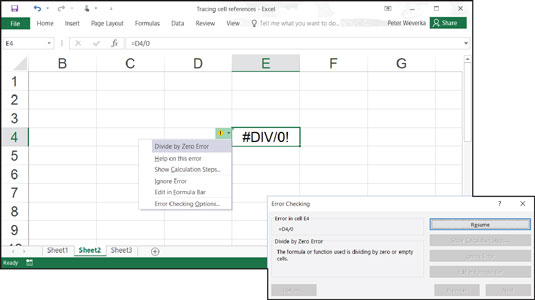
Excel 2016 ponúka niekoľko efektívnych spôsobov, ako opraviť chyby vo vzorcoch. Opravy môžete vykonávať po jednom, spustiť kontrolu chýb a sledovať odkazy na bunky.
V niektorých prípadoch Outlook ukladá e-mailové správy, úlohy a plánované činnosti staršie ako šesť mesiacov do priečinka Archív – špeciálneho priečinka pre zastarané položky. Učte sa, ako efektívne archivovať vaše položky v Outlooku.
Word vám umožňuje robiť rôzne zábavné veci s tabuľkami. Učte sa o vytváraní a formátovaní tabuliek vo Worde 2019. Tabuľky sú skvelé na organizáciu informácií.
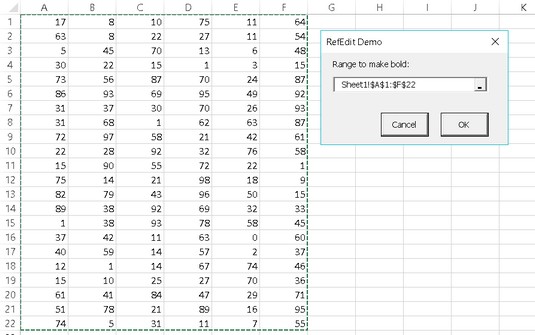
V článku sa dozviete, ako umožniť používateľovi vybrať rozsah v Excel VBA pomocou dialógového okna. Získajte praktické tipy a príklady na zlepšenie práce s rozsahom Excel VBA.
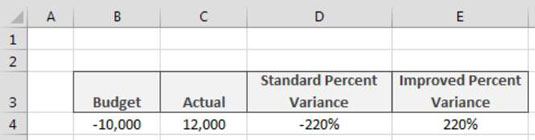
Vzorec na výpočet percentuálnej odchýlky v Exceli s funkciou ABS pre správne výsledky aj so zápornými hodnotami.