Ako zmeniť pozadie v PowerPointe 2019
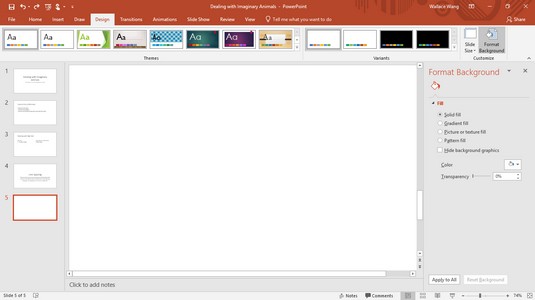
Naučte sa, ako jednoducho zmeniť pozadie v PowerPointe 2019, aby vaše prezentácie pôsobili pútavo a profesionálne. Získajte tipy na plnú farbu, prechod, obrázky a vzory.
Svet štatistík je plný nástrah, no zároveň je plný príležitostí. Či už ste používateľom štatistík alebo niekto, kto ich musí interpretovať, môžete sa dostať do úskalí. Dá sa okolo nich aj prejsť. Tu je desať tipov a pascí z oblasti testovania hypotéz, regresie, korelácie a grafu.
Význam je v mnohých ohľadoch zle zvolený pojem. Keď štatistický test prinesie významný výsledok a rozhodnutie je zamietnuť H0, nezaručuje to, že štúdia za údajmi je dôležitá. Štatistika môže len pomôcť pri rozhodovaní o číslach a záveroch o procesoch, ktoré ich vytvorili. Nemôžu urobiť tieto procesy dôležitými alebo otrasnými. Dôležitosť je niečo, čo musíte posúdiť sami - a to za vás nemôže urobiť žiadny štatistický test.
Pri pokuse o prispôsobenie regresného modelu bodovému grafu je pokušením okamžite použiť čiaru. Toto je najlepšie pochopený regresný model, a keď to pochopíte, sklony a priesečníky nie sú až také skľučujúce.
Lineárna regresia však nie je jediným druhom regresie. Je možné umiestniť krivku cez bodový graf. Nenechajte sa zmiasť: Štatistické pojmy stojace za krivočiarou regresiou sú ťažšie pochopiteľné ako pojmy za lineárnou regresiou.
Stojí však za to venovať čas zvládnutiu týchto konceptov. Niekedy sa krivka hodí oveľa lepšie ako čiara.
Či už pracujete s lineárnou regresiou alebo krivočiarou regresiou, majte na pamäti, že je nevhodné zovšeobecňovať za hranice bodového grafu.
Predpokladajme, že ste vytvorili solídny prediktívny vzťah medzi testom matematických schopností a výkonom v kurzoch matematiky a váš bodový graf pokrýva iba úzky rozsah matematických schopností. Nemáte možnosť zistiť, či vzťah presahuje tento rozsah. Predpovede mimo tohto rozsahu nie sú platné.
Najlepším riešením je rozšíriť rozptyl testovaním viacerých ľudí. Možno zistíte, že pôvodný vzťah rozpráva len časť príbehu.
Dôkladná analýza rezíduí (rozdielov medzi pozorovanými a predpokladanými hodnotami) vám môže veľa povedať o tom, ako dobre sa čiara zhoduje s údajmi. Základným predpokladom je, že variabilita okolo regresnej priamky je rovnaká hore aj dole po priamke. Ak nie, model nemusí byť taký prediktívny, ako si myslíte. Ak je variabilita systematická (väčšia variabilita na jednom konci ako na druhom), krivková regresia môže byť vhodnejšia ako lineárna. Štandardná chyba odhadu nebude vždy ukazovateľom.
Verte či nie, pri korelačných koeficientoch sa to niekedy stáva. Veľmi veľká vzorka môže spôsobiť, že malý korelačný koeficient bude štatisticky významný.
Čo však tento korelačný koeficient skutočne znamená? Koeficient determinácie —r2 — je len 0,038, čo znamená, že SSregresia je menšia ako 4 percentá SSTotal. To je veľmi malá asociácia.
Zrátané a podčiarknuté: Pri pohľade na korelačný koeficient si uvedomte veľkosť vzorky. Ak je dostatočne veľká, môže sa triviálna asociácia ukázať ako štatisticky významná. (Hmmm... význam – je to tu znova!)
Keď sa pozriete na graf, uistite sa, že viete, čo je na každej osi. Uistite sa, že rozumiete merným jednotkám. Rozumiete nezávislej premennej? Rozumiete závislej premennej? Môžete každú z nich opísať vlastnými slovami? Ak je odpoveď na niektorú z týchto otázok „Nie“, nerozumiete grafu, na ktorý sa pozeráte.
Keď sa pozeráte na graf v televíznej reklame, buďte veľmi opatrní, ak zmizne príliš rýchlo, kým neuvidíte, čo je na osiach. Inzerent sa môže pokúšať vytvoriť pretrvávajúci falošný dojem o falošnom vzťahu v grafe. Grafický vzťah môže byť rovnako platný ako ten ďalší základ televíznej reklamy – vedecký dôkaz prostredníctvom animovaného filmu: Drobné animované kefky na čistenie kreslených zubov vám nemusia nevyhnutne zaručiť belšie zuby, ak si produkt kúpite.
Takže ste takmer pripravení súťažiť vo svetovej sérii kameň-papier-nožnice. V rámci prípravy na tento medzinárodný turnaj ste spočítali všetky svoje zápasy za posledných desať rokov a uviedli, koľko percent ste vyhrali, keď ste hrali každú rolu.
Ak chcete zhrnúť všetky výsledky, použite grafické možnosti programu Excel na vytvorenie grafu.
Toľko ľudí vytvára tieto druhy grafov - ľudí, ktorí by to mali vedieť lepšie. Čiara v grafe naznačuje kontinuitu z jedného bodu do druhého. S týmito údajmi je to samozrejme nemožné. Čo je medzi kameňom a papierom? Prečo sú od seba rovnaké jednotky? Prečo sú tri kategórie v tomto poradí?
Jednoducho povedané, čiarový graf nie je správnym grafom, ak aspoň jedna z vašich premenných je množinou kategórií. Namiesto toho vytvorte stĺpcový graf. Funguje tu aj koláčový graf, pretože údaje sú percentá a máte len niekoľko výrezov.
Keď body v grafe predstavujú priemer, uistite sa, že graf obsahuje štandardnú chybu každého priemeru. To dáva divákovi predstavu o variabilite údajov – čo je dôležitý aspekt údajov.
Prostriedky samy o sebe vám nie vždy povedia celý príbeh. Využite každú príležitosť na preskúmanie rozptylov a štandardných odchýlok. Môžete nájsť nejaké skryté nugety. Systematické variácie – napríklad vysoké hodnoty rozptylu spojené s veľkými prostriedkami – môžu byť kľúčom k vzťahu, ktorý ste predtým nevideli.
Ak to so štatistickou prácou myslíte vážne, pravdepodobne budete mať príležitosť nahliadnuť do jedného alebo dvoch štatistických textov. Majte na pamäti, že symboly v niektorých oblastiach štatistiky nie sú štandardné.
Prepojenie pojmov z učebnice so štatistickými funkciami Excelu môže byť náročné kvôli textom a kvôli Excelu. Správy v dialógových oknách a súboroch pomocníka môžu obsahovať iné symboly, ako tie, o ktorých ste čítali, alebo môžu používať rovnaké symboly, ale iným spôsobom. Táto nezrovnalosť môže viesť k nesprávnemu zadávaniu parametra v dialógovom okne, čo vedie k chybe, ktorú je ťažké vysledovať.
Naučte sa, ako jednoducho zmeniť pozadie v PowerPointe 2019, aby vaše prezentácie pôsobili pútavo a profesionálne. Získajte tipy na plnú farbu, prechod, obrázky a vzory.
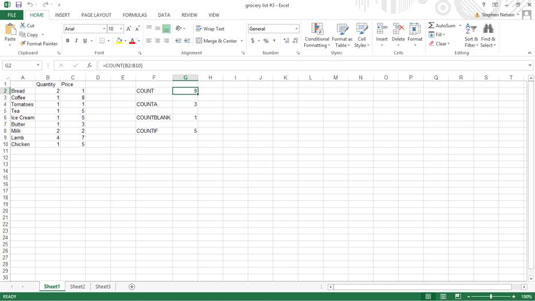
Excel poskytuje štyri užitočné štatistické funkcie na počítanie buniek v hárku alebo zozname: COUNT, COUNTA, COUNTBLANK a COUNTIF. Pre viac informácií o Excel funkciách, pokračujte.
Objavte efektívne klávesové skratky v Exceli 2013 pre zobrazenie, ktoré vám pomôžu zlepšiť produktivitu. Všetky skratky sú začiatkom s Alt+W.
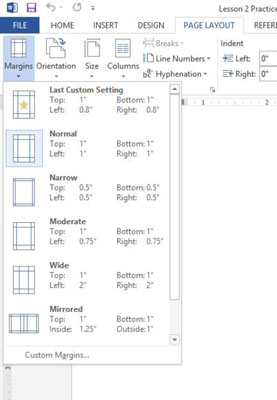
Naučte sa, ako nastaviť okraje v programe Word 2013 s naším jednoduchým sprievodcom. Tento článok obsahuje užitočné tipy a predvoľby okrajov pre váš projekt.
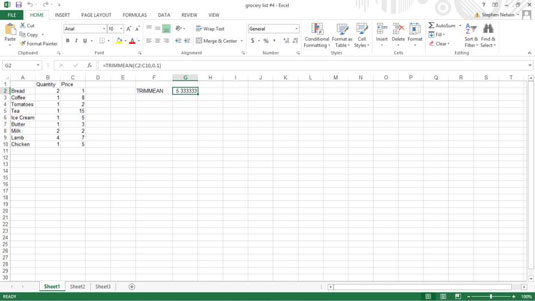
Excel vám poskytuje niekoľko štatistických funkcií na výpočet priemerov, režimov a mediánov. Pozrite si podrobnosti a príklady ich použitia.
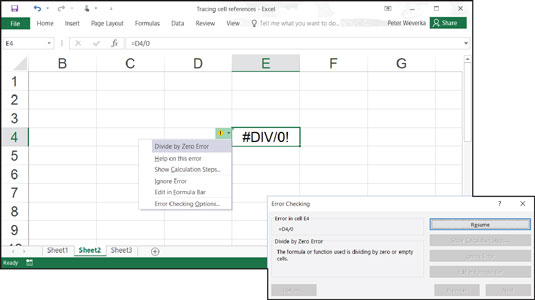
Excel 2016 ponúka niekoľko efektívnych spôsobov, ako opraviť chyby vo vzorcoch. Opravy môžete vykonávať po jednom, spustiť kontrolu chýb a sledovať odkazy na bunky.
V niektorých prípadoch Outlook ukladá e-mailové správy, úlohy a plánované činnosti staršie ako šesť mesiacov do priečinka Archív – špeciálneho priečinka pre zastarané položky. Učte sa, ako efektívne archivovať vaše položky v Outlooku.
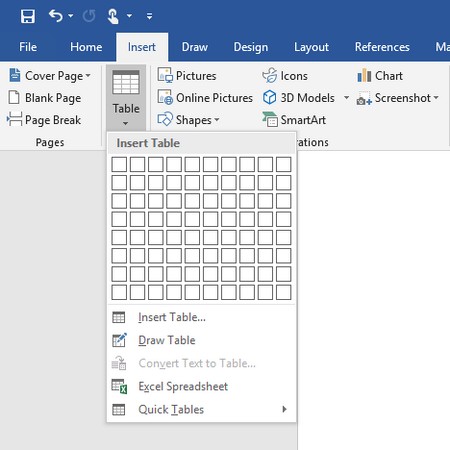
Word vám umožňuje robiť rôzne zábavné veci s tabuľkami. Učte sa o vytváraní a formátovaní tabuliek vo Worde 2019. Tabuľky sú skvelé na organizáciu informácií.
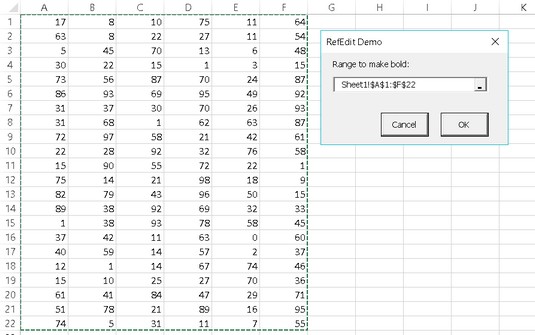
V článku sa dozviete, ako umožniť používateľovi vybrať rozsah v Excel VBA pomocou dialógového okna. Získajte praktické tipy a príklady na zlepšenie práce s rozsahom Excel VBA.
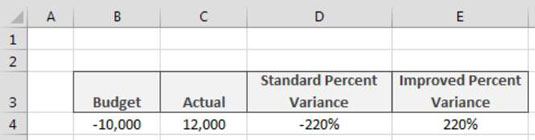
Vzorec na výpočet percentuálnej odchýlky v Exceli s funkciou ABS pre správne výsledky aj so zápornými hodnotami.