Kako dokazati besedilo v tujem jeziku v Wordu 2016
V interesu kozmopolitizma vam Word 2016 omogoča delo s tujimi jeziki. Naučite se, kako vnesti in urediti besedilo v tujem jeziku, ter preveriti črkovanje in slovnico.
Funkcije PV (trenutna vrednost), NPV (neto sedanja vrednost) in FV (prihodnja vrednost) v Excelu 2016, ki jih najdete v spustnem meniju gumba Finance na zavihku Formule traku (Alt+MI), vam omogočajo določitev dobičkonosnosti. naložbe.
Funkcija PV ali sedanja vrednost vrne sedanjo vrednost naložbe, ki je skupni znesek, ki je trenutno vreden niz prihodnjih plačil. Sintaksa funkcije PV je naslednja:
=PV(stopnja,nper,pmt,[fv],[vrsta])
V FV in tipa trditve so fakultativni argumenti v funkciji (s oglatih oklepajih naveden). Fv argument je prihodnja vrednost ali denarnih sredstev, ki jih želite imeti, potem ko si zadnje plačilo. Če izpustite argument fv , Excel prevzame prihodnjo vrednost nič (0). Tipa argument navaja, ali se plačilo izvede na začetku ali na koncu obdobja: Enter 0 (ali izpustite tipa argument), ko je plačilo na koncu obdobja, in uporabo 1, ko se je na začetku obdobje.
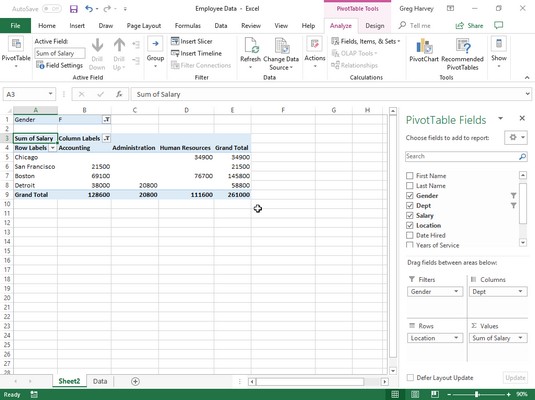
Naslednja slika vsebuje več primerov uporabe PV funkcije. Vse tri PV funkcije uporabljajo enako letno odstotno stopnjo 1,25 odstotka in obdobje 10 let. Ker se plačila izvajajo mesečno, vsaka funkcija te letne zneske pretvori v mesečne. Na primer, v funkciji PV v celici E3 se letna obrestna mera v celici A3 pretvori v mesečno z deljenjem z 12 (A3/12). Letno obdobje v celici B3 se pretvori v enakovredna mesečna obdobja z množenjem z 12 (B3 x 12).
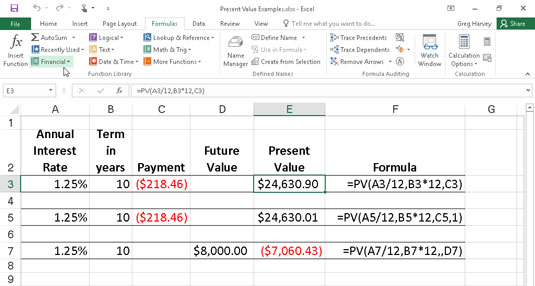
Uporaba PV funkcije za izračun sedanje vrednosti različnih naložb.
Upoštevajte, da čeprav funkcije PV v celicah E3 in E5 uporabljajo argumente rate, nper in pmt (218,46 $), so njihovi rezultati nekoliko drugačni. To je posledica razlike v argumentu tipa v obeh funkcijah: funkcija PV v celici E3 predpostavlja, da se vsako plačilo izvede na koncu obdobja ( argument tipa je 0, kadar je izpuščen), medtem ko funkcija PV v celica E5 predvideva, da se vsako plačilo izvede na začetku obdobja (označeno z argumentom tipa 1). Ko je plačilo izvedeno na začetku obdobja, je sedanja vrednost te naložbe 0,89 USD višja kot pri plačilu na koncu obdobja, kar odraža obresti, obračunane v zadnjem obdobju.
Tretji primer v celici E7 (prikazano na sliki 4-1) uporablja funkcijo PV z argumentom fv namesto argumenta pmt . V tem primeru funkcija PV navaja, da bi morali mesečno plačevati 7.060,43 $ za 10-letno obdobje, da bi dosegli denarni saldo v višini 8.000 $, ob predpostavki, da je naložba vračala stalno letno obrestno mero 1 1/4 odstotka. Upoštevajte, da če uporabljate funkcijo PV z argumentom fv namesto argumenta pmt , morate še vedno navesti položaj argumenta pmt v funkciji z vejico (torej dve vejici v vrstici v funkciji), da bo Excel ne Ne zamenjajte svojega argumenta fv z argumentom pmt .
Funkcija NPV izračuna neto sedanjo vrednost na podlagi vrste denarnih tokov. Sintaksa te funkcije je
=NPV( stopnja , vrednost1 ,[ vrednost2 ],[...])
kjer so vrednost1, vrednost2 in tako naprej med 1 in 13 vrednostnimi argumenti, ki predstavljajo vrsto plačil (negativne vrednosti) in dohodka (pozitivne vrednosti), od katerih je vsak enako časovno razporejen in se pojavi na koncu obdobja. Naložba NPV se začne eno obdobje pred obdobjem denarnega toka vrednosti1 in se konča z zadnjim denarnim tokom na seznamu argumentov. Če se vaš prvi denarni tok pojavi na začetku obdobja, ga morate dodati rezultatu funkcije NPV in ne vključiti kot enega od argumentov.
Naslednja slika prikazuje uporabo funkcije NPV za oceno privlačnosti petletne naložbe, ki zahteva začetno naložbo 30.000 $ (vrednost v celici G3). Prvo leto pričakujete izgubo v višini 22.000 $ (celica B3); drugo leto dobiček 15.000 $ (celica C3); tretje leto dobiček 25.000 $ (celica D3); četrto leto dobiček 32.000 $ (celica E3); in peto leto dobiček 38.000 $ (celica F3). Upoštevajte, da se te reference celic uporabljajo kot vrednostni argumenti funkcije NPV.
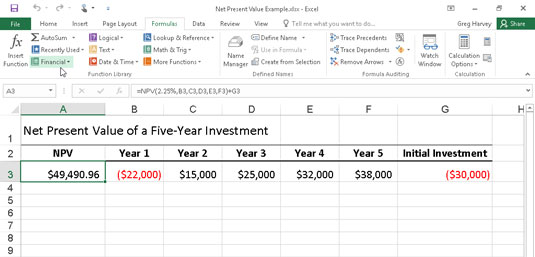
Uporaba funkcije NPV za izračun neto sedanje vrednosti naložbe.
Za razliko od uporabe funkcije PV, funkcija NPV ne zahteva enakomernega toka denarnih tokov. Stopnja argument v funkciji znaša 2,25 odstotka. V tem primeru to predstavlja diskontno stopnjo naložbe – to je obrestno mero, ki jo lahko pričakujete v petletnem obdobju, če svoj denar vložite v kakšno drugo vrsto naložbe, kot je denar z visokim donosom. -tržni račun. Ta funkcija NPV v celici A3 vrne neto sedanjo vrednost 49.490,96 $, kar kaže, da lahko pričakujete, da boste z vlaganjem svojih 30.000 $ v to naložbo dosegli veliko več, kot bi morda lahko z vlaganjem denarja na račun denarnega trga po obrestni meri 2,25 odstotka.
Funkcija FV izračuna prihodnjo vrednost naložbe. Sintaksa te funkcije je
=FV(stopnja,nper,pmt,[pv],[vrsta])
V , NPER, PMT, hitrost in tip trditve so enaki kot tisti, ki ga funkcija PV uporablja. Pv argument je sedanja vrednost ali pavšalno znesek, za katerega želite izračunati vrednost v prihodnosti. Tako kot pri argumentih fv in type v funkciji PV sta tudi argumenta pv in type v funkciji FV neobvezna. Če te argumente izpustite, Excel predvideva, da so njihove vrednosti nič (0) v funkciji.
Funkcijo FV lahko uporabite za izračun prihodnje vrednosti naložbe, kot je IRA (Individual Retirement Account). Recimo, da boste ustanovili IRA pri starosti 43 let in se boste upokojili čez 22 let pri starosti 65 let in da nameravate na začetku vsakega leta opraviti letna plačila v IRA. Če predvidevate stopnjo donosa 2,5 odstotka na leto, bi v svoj delovni list vnesli naslednjo funkcijo FV:
=FV(2,5%,22,–1500,,1)
Excel nato navede, da lahko pričakujete prihodnjo vrednost 44.376,64 $ za vaš IRA, ko se upokojite pri starosti 65 let. Če ste IRA ustanovili leto prej in račun že ima sedanjo vrednost 1.538 $, bi funkcijo FV spremenili na naslednji način :
=FV(2,5%,22,–1500,–1538,1)
V tem primeru Excel kaže, da lahko pričakujete prihodnjo vrednost 47.024,42 $ za vašo IRA ob upokojitvi.
V interesu kozmopolitizma vam Word 2016 omogoča delo s tujimi jeziki. Naučite se, kako vnesti in urediti besedilo v tujem jeziku, ter preveriti črkovanje in slovnico.
Učinkovito filtriranje in razvrščanje podatkov v vrtilni tabeli Excel 2019 za boljša poročila. Dosežite hitrejše analize z našimi namigi in triki!
Reševalec v Excelu je močno orodje za optimizacijo, ki lahko naleti na težave. Razumevanje sporočil o napakah reševalca vam lahko pomaga rešiti težave in optimizirati vaše matematične modele.
Odkrijte različne <strong>teme PowerPoint 2019</strong> in kako jih lahko uporabite za izboljšanje vaših predstavitev. Izberite najboljšo temo za vaše diapozitive.
Nekateri statistični ukrepi v Excelu so lahko zelo zmedeni, vendar so funkcije hi-kvadrat res praktične. Preberite vse opise funkcij hi-kvadrat za bolje razumevanje statističnih orodij.
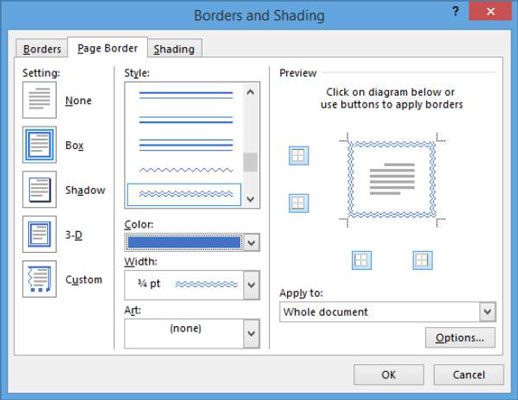
V tem članku se naučite, kako dodati <strong>obrobo strani</strong> v Word 2013, vključno z različnimi slogi in tehnikami za izboljšanje videza vaših dokumentov.
Ni vam treba omejiti uporabe urejevalnika besedil na delo z enim samim dokumentom. Učinkovito delajte z več dokumenti v Wordu 2013.
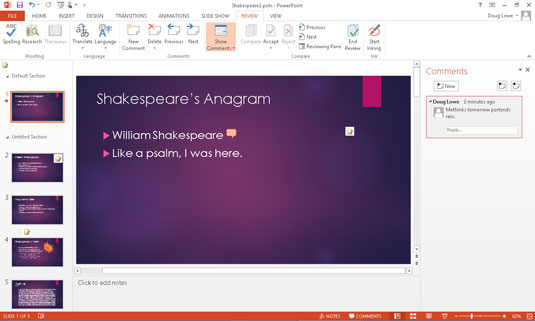
Sodelovanje pri predstavitvi, ustvarjeni v PowerPointu 2013, je lahko tako preprosto kot dodajanje komentarjev. Odkrijte, kako učinkovito uporabljati komentarje za izboljšanje vaših predstavitev.
Ugotovite, kako prilagoditi nastavitve preverjanja črkovanja in slovnice v Wordu 2016, da izboljšate svoje jezikovne sposobnosti.
PowerPoint 2013 vam ponuja različne načine za izvedbo predstavitve, vključno s tiskanjem izročkov. Izročki so ključnega pomena za izboljšanje vaše predstavitve.