Funktionerne PV (nutidsværdi), NPV (nettoværdi) og FV (fremtidig værdi) i Excel 2016 findes alle på finansknappens rullemenu på båndets formler-fane (Alt+MI) gør det muligt for dig at bestemme rentabiliteten af en investering.
Funktionen PV eller nutidsværdi returnerer nutidsværdien af en investering, som er det samlede beløb, som en række fremtidige betalinger er værd i øjeblikket. Syntaksen for PV-funktionen er som følger:
=PV(rate,nper,pmt,[fv],[type])
De fv og typen argumenter er valgfri argumenter i funktionen (angivet i de firkantede parenteser). Den fv argument er den fremtidige værdi eller kassebeholdning, som du vil have efter at din sidste betaling. Hvis du udelader fv- argumentet, antager Excel en fremtidig værdi på nul (0). Den typen argument angiver, om betalingen foretages i begyndelsen eller slutningen af perioden: Indtast 0 (eller udelader typen argument) når betalingen sker ved afslutningen af perioden, og bruge 1, hvor den afgives i begyndelsen af perioden.
Den følgende figur indeholder flere eksempler på brug af PV-funktionen. Alle tre PV-funktioner bruger den samme årlige procentsats på 1,25 procent og løbetid på 10 år. Fordi betalinger foretages månedligt, konverterer hver funktion disse årlige tal til månedlige tal. For eksempel, i PV-funktionen i celle E3 omregnes den årlige rente i celle A3 til en månedlig rente ved at dividere med 12 (A3/12). Den årlige periode i celle B3 omregnes til ækvivalente månedlige perioder ved at gange med 12 (B3 x 12).
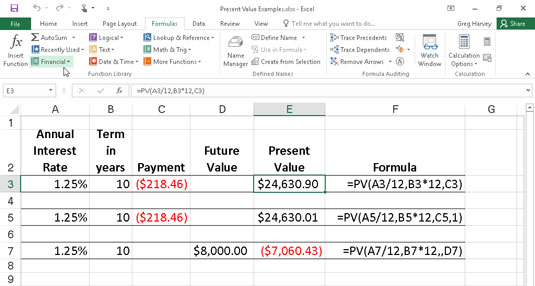
Brug af PV-funktionen til at beregne nutidsværdien af forskellige investeringer.
Bemærk, at selvom PV-funktionerne i cellerne E3 og E5 bruger argumenterne rate, nper og pmt ($218,46), er deres resultater lidt anderledes. Dette er forårsaget af forskellen i typen argument i de to funktioner: PV funktion i celle E3 antager, at hver betaling foretages ved afslutningen af perioden (den typen argument er 0, når den er udeladt), mens PV funktion i celle E5 antager, at hver betaling foretages ved begyndelsen af perioden (angivet med en typen argument 1). Når betalingen foretages i begyndelsen af perioden, er nutidsværdien af denne investering $0,89 højere, end når betalingen foretages i slutningen af perioden, hvilket afspejler de påløbne renter i den sidste periode.
Det tredje eksempel i celle E7 (vist i figur 4-1) bruger PV-funktionen med et fv- argument i stedet for pmt- argumentet. I dette eksempel angiver PV-funktionen, at du skulle foretage månedlige betalinger på 7.060,43 USD i en 10-årig periode for at realisere en kassebeholdning på 8.000 USD, forudsat at investeringen gav en konstant årlig rente på 1 1/4 procent. Bemærk, at når du bruger PV-funktionen med fv- argumentet i stedet for pmt- argumentet, skal du stadig angive positionen af pmt- argumentet i funktionen med et komma (altså de to kommaer i træk i funktionen), så Excel ikke Forveksle ikke dit fv- argument med pmt- argumentet.
NPV-funktionen beregner nutidsværdien baseret på en række pengestrømme. Syntaksen for denne funktion er
=NPV( rate , value1 ,[ value2 ],[...])
hvor værdi1, værdi2 og så videre er mellem 1 og 13 værdiargumenter, der repræsenterer en række betalinger (negative værdier) og indkomst (positive værdier), som hver er ligeligt fordelt i tid og forekommer i slutningen af perioden. NPV-investeringen begynder en periode før perioden for værdi1- pengestrømmen og slutter med den sidste pengestrøm i argumentlisten. Hvis dit første pengestrøm opstår i begyndelsen af perioden, skal du tilføje det til resultatet af NPV-funktionen i stedet for at inkludere det som et af argumenterne.
Følgende figur illustrerer brugen af NPV-funktionen til at evaluere attraktiviteten af en femårig investering, der kræver en initial investering på $30.000 (værdien i celle G3). Det første år forventer du et tab på $22.000 (celle B3); det andet år, et overskud på $15.000 (celle C3); det tredje år, et overskud på $25.000 (celle D3); det fjerde år, et overskud på $32.000 (celle E3); og det femte år et overskud på $38.000 (celle F3). Bemærk, at disse cellereferencer anvendes som værdi argumenter NPV-funktionen.
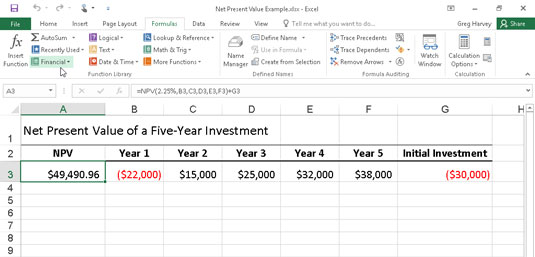
Brug af NPV-funktionen til at beregne nutidsværdien af en investering.
I modsætning til når du bruger PV-funktionen, kræver NPV-funktionen ikke en jævn strøm af pengestrømme. Den sats argument i funktionen er fastsat til 2,25 procent. I dette eksempel repræsenterer dette investeringens diskonteringsrente - det vil sige den rente, som du kan forvente at få i løbet af femårsperioden, hvis du sætter dine penge i en anden form for investering, såsom højafkastpenge -markedskonto. Denne NPV-funktion i celle A3 returnerer en nettonutidsværdi på 49.490,96 USD, hvilket indikerer, at du kan forvente at få meget mere ud af at investere dine 30.000 USD i denne investering, end du overhovedet kunne ved at investere pengene på en pengemarkedskonto til renten. på 2,25 pct.
FV-funktionen beregner den fremtidige værdi af en investering. Syntaksen for denne funktion er
=FV(rate;nper;pmt;[pv],[type])
De sats, nper, PMT, og typen argumenter er de samme som dem, der anvendes af PV funktion. Den pv argument er nutidsværdien eller engangsbeløb beløb, som du ønsker at beregne den fremtidige værdi. Som med argumenterne fv og type i PV-funktionen, er både argumenterne pv og type valgfrie i FV-funktionen. Hvis du udelader disse argumenter, antager Excel, at deres værdier er nul (0) i funktionen.
Du kan bruge FV-funktionen til at beregne den fremtidige værdi af en investering, såsom en IRA (Individual Retirement Account). Antag for eksempel, at du etablerer en IRA i en alder af 43 og går på pension om 22 år i en alder af 65, og at du planlægger at foretage årlige indbetalinger til IRA i begyndelsen af hvert år. Hvis du antager et afkast på 2,5 procent om året, vil du indtaste følgende FV-funktion i dit regneark:
=FV(2,5 %;22;–1500;,1)
Excel angiver derefter, at du kan forvente en fremtidig værdi på 44.376,64 USD for din IRA, når du går på pension som 65-årig. Hvis du havde etableret IRA et år før, og kontoen allerede har en nutidsværdi på 1.538 USD, ville du ændre FV-funktionen som følger :
=FV(2,5 %;22;–1500;–1538;1)
I dette tilfælde indikerer Excel, at du kan forvente en fremtidig værdi på $47.024,42 for din IRA ved pensionering.
Sådan blokerer du Microsoft Word fra at åbne filer i skrivebeskyttet tilstand på Windows Microsoft Word åbner filer i skrivebeskyttet tilstand, hvilket gør det umuligt at redigere det? Bare rolig, metoderne er nedenfor
Sådan rettes fejl ved udskrivning af forkerte Microsoft Word-dokumenter Fejl ved udskrivning af Word-dokumenter med ændrede skrifttyper, rodede afsnit, manglende tekst eller tabt indhold er ret almindelige. Men lad være
Hvis du har brugt pennen eller highlighteren til at tegne på dine PowerPoint-dias under en præsentation, kan du gemme tegningerne til næste præsentation eller slette dem, så næste gang du viser den, starter du med rene PowerPoint-dias. Følg disse instruktioner for at slette pen- og highlighter-tegninger: Sletning af linjer en ved […]
Style-biblioteket indeholder CSS-filer, Extensible Stylesheet Language-filer (XSL) og billeder, der bruges af foruddefinerede mastersider, sidelayouts og kontrolelementer i SharePoint 2010. For at finde CSS-filer i Style-biblioteket på et udgivelsessted: Vælg Site Actions→ View Alt webstedsindhold. Indholdet af webstedet vises. Style-biblioteket ligger i […]
Overvæld ikke dit publikum med gigantiske tal. I Microsoft Excel kan du forbedre læsbarheden af dine dashboards og rapporter ved at formatere dine tal, så de vises i tusinder eller millioner.
Lær, hvordan du bruger SharePoints sociale netværksværktøjer, der lader enkeltpersoner og grupper kommunikere, samarbejde, dele og forbinde.
Julianske datoer bruges ofte i produktionsmiljøer som et tidsstempel og hurtig reference for et batchnummer. Denne type datokodning giver detailhandlere, forbrugere og serviceagenter mulighed for at identificere, hvornår et produkt blev fremstillet, og dermed produktets alder. Julianske datoer bruges også i programmering, militæret og astronomi. Forskellige […]
Du kan oprette en webapp i Access 2016. Så hvad er en webapp overhovedet? Nå, web betyder, at det er online, og app er kun en forkortelse for "applikation". En Custom Web App er en online databaseapplikation, der tilgås fra skyen ved hjælp af en browser. Du bygger og vedligeholder webappen i desktopversionen […]
De fleste sider i SharePoint 2010 viser en liste over navigationslinks på linjen Hurtig start langs venstre side af siden. Hurtig startlinjen viser links til fremhævet webstedsindhold såsom lister, biblioteker, websteder og udgivelsessider. Hurtigstartlinjen indeholder to meget vigtige links: Linket Alt webstedsindhold: […]
Ved simple problemer finder Solver i Excel som regel hurtigt de optimale Solver-variableværdier for objektivfunktionen. Men i nogle tilfælde har Solver problemer med at finde de Solver-variableværdier, der optimerer objektivfunktionen. I disse tilfælde viser Solver typisk en meddelelse eller en fejlmeddelelse, der beskriver eller diskuterer det problem, der […]
