En matrixformel i Excel 2013 (og andre regneark) er en speciel formel, der fungerer på en række værdier. Hvis et celleområde leverer dette område (som det ofte er tilfældet), omtales det som et matrixområde . Hvis dette område leveres af en liste over numeriske værdier, er de kendt som en matrixkonstant .
Mange regnearkstabeller bruger en original formel, som du kopierer til tilstødende celler ved at bruge relative cellereferencer (nogle gange omtalt som en en-til-mange kopi ). I nogle tilfælde kan du bygge den originale formel, så Excel udfører den ønskede beregning ikke kun i den aktive celle, men også i alle de andre celler, som du normalt ville kopiere formlen til. Det gør du ved at oprette en matrixformel .
Selvom array-konceptet kan virke fremmed i starten, er du virkelig godt bekendt med arrays, fordi kolonne-og-rækkestrukturen i Excel-regnearkgitteret naturligt organiserer dine dataområder i endimensionelle og todimensionale arrays. (1-D-arrays fylder en enkelt række eller kolonne, mens 2-D-arrays fylder flere rækker og kolonner).
Den følgende figur illustrerer et par todimensionelle arrays med numeriske indtastninger af to forskellige størrelser. Det første array er et 3 x 2 array i celleområdet B2:C4. Denne matrix er en 3 x 2 matrix, fordi den optager tre rækker og to kolonner.
Det andet array er et 2 x 3 array i celleområdet F2:H3. Denne matrix er en 2 x 3 matrix, fordi den bruger to rækker og tre kolonner.
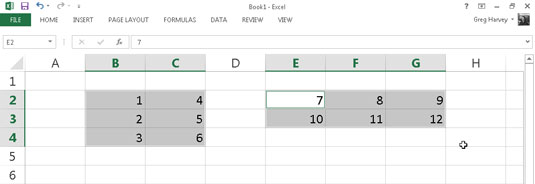
Hvis du skulle angive værdierne i den første 3 x 2 matrix som en matrixkonstant i en formel, ville de fremstå som følger:
{1,4;2,5;3,6}
Flere ting på denne liste er bemærkelsesværdige. Først er matrixkonstanten indesluttet i et par parenteser ({}). For det andet er kolonner i hver række adskilt af kommaer (,), og rækker i arrayet er adskilt af semikolon (;). For det tredje vises konstanterne i arrayet på tværs af hver række og derefter ned i hver kolonne og ikke ned i hver kolonne og på tværs af hver række.
Den anden 2 x 3 matrix udtrykt som en matrixkonstant ser ud som følger:
{7,8,9;10,11,12}
Bemærk igen, at du angiver værdierne på tværs af hver række og derefter ned i hver kolonne, hvor du adskiller værdierne i forskellige kolonner med kommaer og værdierne i forskellige rækker med et semikolon.
Brugen af matrixformler kan betydeligt reducere mængden af formelkopiering, som du skal udføre i et regneark, ved at producere flere resultater i hele matrixområdet i en enkelt handling.
Derudover bruger matrixformler mindre computerhukommelse end standardformler, der kopieres i et interval. Dette kan være vigtigt, når du laver et stort regneark med mange tabeller, fordi det kan betyde forskellen mellem at passe alle dine beregninger på ét regneark og at skulle opdele din model i flere regnearksfiler.
Sådan blokerer du Microsoft Word fra at åbne filer i skrivebeskyttet tilstand på Windows Microsoft Word åbner filer i skrivebeskyttet tilstand, hvilket gør det umuligt at redigere det? Bare rolig, metoderne er nedenfor
Sådan rettes fejl ved udskrivning af forkerte Microsoft Word-dokumenter Fejl ved udskrivning af Word-dokumenter med ændrede skrifttyper, rodede afsnit, manglende tekst eller tabt indhold er ret almindelige. Men lad være
Hvis du har brugt pennen eller highlighteren til at tegne på dine PowerPoint-dias under en præsentation, kan du gemme tegningerne til næste præsentation eller slette dem, så næste gang du viser den, starter du med rene PowerPoint-dias. Følg disse instruktioner for at slette pen- og highlighter-tegninger: Sletning af linjer en ved […]
Style-biblioteket indeholder CSS-filer, Extensible Stylesheet Language-filer (XSL) og billeder, der bruges af foruddefinerede mastersider, sidelayouts og kontrolelementer i SharePoint 2010. For at finde CSS-filer i Style-biblioteket på et udgivelsessted: Vælg Site Actions→ View Alt webstedsindhold. Indholdet af webstedet vises. Style-biblioteket ligger i […]
Overvæld ikke dit publikum med gigantiske tal. I Microsoft Excel kan du forbedre læsbarheden af dine dashboards og rapporter ved at formatere dine tal, så de vises i tusinder eller millioner.
Lær, hvordan du bruger SharePoints sociale netværksværktøjer, der lader enkeltpersoner og grupper kommunikere, samarbejde, dele og forbinde.
Julianske datoer bruges ofte i produktionsmiljøer som et tidsstempel og hurtig reference for et batchnummer. Denne type datokodning giver detailhandlere, forbrugere og serviceagenter mulighed for at identificere, hvornår et produkt blev fremstillet, og dermed produktets alder. Julianske datoer bruges også i programmering, militæret og astronomi. Forskellige […]
Du kan oprette en webapp i Access 2016. Så hvad er en webapp overhovedet? Nå, web betyder, at det er online, og app er kun en forkortelse for "applikation". En Custom Web App er en online databaseapplikation, der tilgås fra skyen ved hjælp af en browser. Du bygger og vedligeholder webappen i desktopversionen […]
De fleste sider i SharePoint 2010 viser en liste over navigationslinks på linjen Hurtig start langs venstre side af siden. Hurtig startlinjen viser links til fremhævet webstedsindhold såsom lister, biblioteker, websteder og udgivelsessider. Hurtigstartlinjen indeholder to meget vigtige links: Linket Alt webstedsindhold: […]
Ved simple problemer finder Solver i Excel som regel hurtigt de optimale Solver-variableværdier for objektivfunktionen. Men i nogle tilfælde har Solver problemer med at finde de Solver-variableværdier, der optimerer objektivfunktionen. I disse tilfælde viser Solver typisk en meddelelse eller en fejlmeddelelse, der beskriver eller diskuterer det problem, der […]
