Her er nogle sandsynlighedsrelaterede regnearksfunktioner, som du kan bruge i Excel 2016 til at hjælpe med statistisk analyse. Selvom de er lidt på den esoteriske side, kan du måske finde noget brug for dem.
Hvis du har en sandsynlighedsfordeling af en diskret stokastisk variabel, og du vil finde sandsynligheden for, at variablen får en bestemt værdi, er PROB noget for dig. Her er dialogboksen PROB Argument Functions sammen med en distribution.
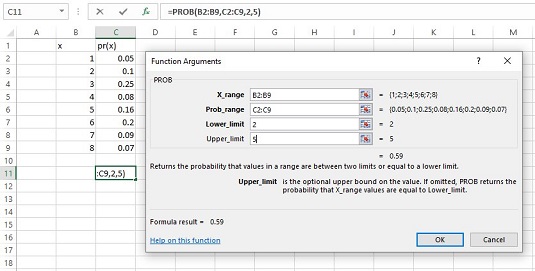
Dialogboksen PROB-funktionsargumenter og en sandsynlighedsfordeling.
Du angiver den tilfældige variabel (X_range), sandsynligheder (Prob_range), en nedre grænse og en øvre grænse. PROB returnerer sandsynligheden for, at den stokastiske variabel antager en værdi mellem disse grænser (inklusive).
Hvis du lader Øvre grænse være tom, returnerer PROB sandsynligheden for den værdi, du gav for den nedre grænse. Hvis du lader den nedre grænse være tom, returnerer SANDSYNLIGHED sandsynligheden for maksimalt at opnå den øvre grænse (f.eks. den kumulative sandsynlighed).
Dette er en sandsynlighedstæthedsfunktion, der for det meste er anvendelig til teknik. Det tjener som model for tiden, indtil et fysisk system svigter. Som ingeniører ved, forbliver antallet af fejl i nogle systemer det samme over tid, fordi stød på systemet forårsager fejl. I andre, ligesom nogle mikroelektroniske komponenter, falder antallet af fejl med tiden. Hos atter andre øger slid og ælde fejl med tiden.
Weibull-fordelingens to parametre gør det muligt at afspejle alle disse muligheder. En parameter, Alpha, bestemmer, hvor bred eller smal fordelingen er. Den anden, Beta, bestemmer, hvor den er centreret på x- aksen.
Weibulls sandsynlighedstæthedsfunktion er en ret kompliceret ligning. Takket være Excel behøver du ikke bekymre dig om det. Billedet nedenfor viser WEIBULL.DISTs funktionsargument-dialogboks.
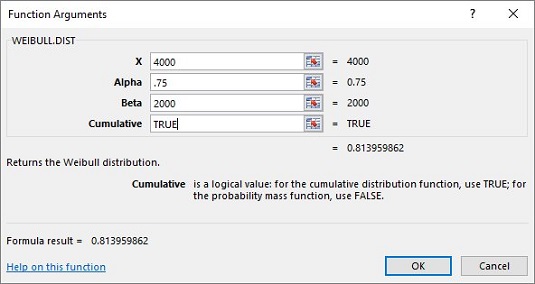
Dialogboksen WEIBULL.DIST Funktionsargumenter.
Dialogboksen besvarer den slags spørgsmål, som en produktingeniør ville stille: Antag, at tiden til svigt af en pære i en LCD-projektor følger en Weibull-fordeling med Alpha = 0,75 og Beta = 2.000 timer. Hvad er sandsynligheden for, at pæren højst holder 4.000 timer? Dialogboksen viser, at svaret er .814.
Sådan blokerer du Microsoft Word fra at åbne filer i skrivebeskyttet tilstand på Windows Microsoft Word åbner filer i skrivebeskyttet tilstand, hvilket gør det umuligt at redigere det? Bare rolig, metoderne er nedenfor
Sådan rettes fejl ved udskrivning af forkerte Microsoft Word-dokumenter Fejl ved udskrivning af Word-dokumenter med ændrede skrifttyper, rodede afsnit, manglende tekst eller tabt indhold er ret almindelige. Men lad være
Hvis du har brugt pennen eller highlighteren til at tegne på dine PowerPoint-dias under en præsentation, kan du gemme tegningerne til næste præsentation eller slette dem, så næste gang du viser den, starter du med rene PowerPoint-dias. Følg disse instruktioner for at slette pen- og highlighter-tegninger: Sletning af linjer en ved […]
Style-biblioteket indeholder CSS-filer, Extensible Stylesheet Language-filer (XSL) og billeder, der bruges af foruddefinerede mastersider, sidelayouts og kontrolelementer i SharePoint 2010. For at finde CSS-filer i Style-biblioteket på et udgivelsessted: Vælg Site Actions→ View Alt webstedsindhold. Indholdet af webstedet vises. Style-biblioteket ligger i […]
Overvæld ikke dit publikum med gigantiske tal. I Microsoft Excel kan du forbedre læsbarheden af dine dashboards og rapporter ved at formatere dine tal, så de vises i tusinder eller millioner.
Lær, hvordan du bruger SharePoints sociale netværksværktøjer, der lader enkeltpersoner og grupper kommunikere, samarbejde, dele og forbinde.
Julianske datoer bruges ofte i produktionsmiljøer som et tidsstempel og hurtig reference for et batchnummer. Denne type datokodning giver detailhandlere, forbrugere og serviceagenter mulighed for at identificere, hvornår et produkt blev fremstillet, og dermed produktets alder. Julianske datoer bruges også i programmering, militæret og astronomi. Forskellige […]
Du kan oprette en webapp i Access 2016. Så hvad er en webapp overhovedet? Nå, web betyder, at det er online, og app er kun en forkortelse for "applikation". En Custom Web App er en online databaseapplikation, der tilgås fra skyen ved hjælp af en browser. Du bygger og vedligeholder webappen i desktopversionen […]
De fleste sider i SharePoint 2010 viser en liste over navigationslinks på linjen Hurtig start langs venstre side af siden. Hurtig startlinjen viser links til fremhævet webstedsindhold såsom lister, biblioteker, websteder og udgivelsessider. Hurtigstartlinjen indeholder to meget vigtige links: Linket Alt webstedsindhold: […]
Ved simple problemer finder Solver i Excel som regel hurtigt de optimale Solver-variableværdier for objektivfunktionen. Men i nogle tilfælde har Solver problemer med at finde de Solver-variableværdier, der optimerer objektivfunktionen. I disse tilfælde viser Solver typisk en meddelelse eller en fejlmeddelelse, der beskriver eller diskuterer det problem, der […]
