Excel er et skønt værktøj, når du skal bruge statistik. Hvis du aldrig har været udsat for statistik i skolen, eller det er et årti eller to siden, du var, så lad disse tips hjælpe dig med at bruge nogle af de statistiske værktøjer, som Excel tilbyder.
Den første ting, du bør vide, er, at nogle statistiske analyser og nogle statistiske mål er temmelig ligetil. Beskrivende statistikker, som inkluderer ting som pivottabellens krydstabeller, såvel som nogle af de statistiske funktioner, giver mening selv for nogen, der ikke er så kvantitative.
Når nogen bruger udtrykket gennemsnit, er det, han normalt refererer til, den mest almindelige gennemsnitsmåling, som er et gennemsnit. At forstå, at udtrykket gennemsnit er upræcist, gør meget af Excels statistiske funktionalitet mere forståelig.
For at gøre denne diskussion mere konkret, antag, at du ser på et lille sæt værdier: 1, 2, 3, 4 og 5. Som du måske ved, er middelværdien i dette lille sæt værdier 3. Du kan beregne middelværdien ved at lægge alle tallene i sættet (1+2+3+4+5) sammen og derefter dividere denne sum (15) med det samlede antal værdier i sættet (5).
Den mediane værdi er den værdi, der adskiller de største værdier fra de mindste værdier. I datasættet 1, 2, 3, 4 og 5 er medianen 3. Værdien 3 adskiller de største værdier (4 og 5) fra de mindste værdier (1 og 2).
Du behøver ikke forstå forskellige gennemsnitsmålinger, men du skal huske, at udtrykket gennemsnit er ret upræcist.
Formlen for standardafvigelse og logikken er ret lette at forstå.
En standardafvigelse beskriver, hvordan værdier i et datasæt varierer omkring middelværdien. Det smarte ved statistiske mål som en standardafvigelse, du får ofte reel indsigt i karakteristikaene af de data, du kigger på. En anden ting er, at med disse to bits af data kan du ofte drage slutninger om data ved at se på prøver.
Observation er et af de udtryk, du vil støde på, hvis du læser noget om statistik. En observation er bare en observation. En måde at definere begrebet observation på er sådan her: Når du rent faktisk tildeler en værdi til en af dine tilfældige variabler, opretter du en observation.
En stikprøve er en samling af observationer fra en population. For eksempel, hvis du opretter et datasæt, der registrerer den daglige høje temperatur i dit nabolag, er din lille samling af observationer et eksempel.
Til sammenligning er en stikprøve ikke en population. En population omfatter alle mulige observationer.
Hvis du ser på et udsnit af værdier fra en population, og stikprøven er repræsentativ og stor nok, kan du drage konklusioner om populationen baseret på karakteristika ved stikprøven.
Inferentiel statistik, selvom den er meget kraftfuld, besidder to kvaliteter, som du har brug for at kende:
Nøjagtighedsproblemer
Stejl indlæringskurve
P robability fordelingsfunktion lyder temmelig tricky; men du kan faktisk intuitivt forstå, hvad en sandsynlighedsfordelingsfunktion er med et par nyttige eksempler.
En almindelig fordeling, som du for eksempel hører om i statistikklasser, er en T-fordeling. En T-fordeling er i det væsentlige en normalfordeling undtagen med tungere, federe haler.
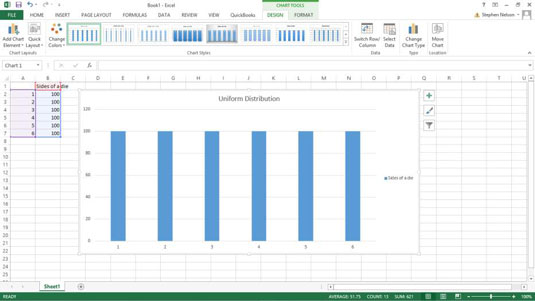
En almindelig sandsynlighedsfordelingsfunktion er en ensartet fordeling. I en ensartet fordeling har hver begivenhed den samme sandsynlighed for at indtræffe. Det unikke ved denne distribution er, at alt er temmelig niveau.
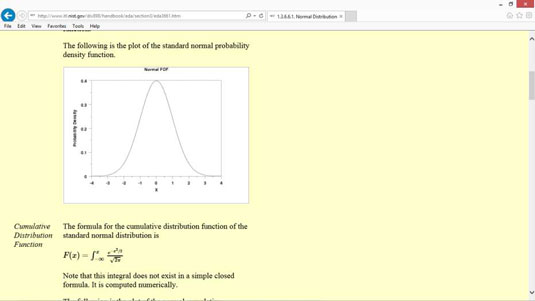
En anden almindelig type sandsynlighedsfordelingsfunktion er normalfordelingen, også kendt som en klokkekurve eller en gaussisk fordeling.
En normalfordeling forekommer naturligt i mange situationer. For eksempel er intelligenskvotienter (IQ'er) normalfordelt.
En parameter er et input til sandsynlighedsfordelingsfunktionen. Med andre ord skal formlen eller funktionen eller ligningen, der beskriver en sandsynlighedsfordelingskurve, have input. I statistik kaldes disse input for parametre.
Nogle sandsynlighedsfordelingsfunktioner behøver kun en enkelt simpel parameter. For at arbejde med en ensartet fordeling f.eks. behøver du kun antallet af værdier i datasættet. En sekssidet terning har for eksempel kun seks muligheder.
Et par andre nyttige statistiske udtryk at kende er skævhed og kurtosis. Skævhed kvantificerer manglen på symmetri i en sandsynlighedsfordeling. I en perfekt symmetrisk fordeling, ligesom normalfordelingen, er skævheden lig med nul. Hvis en sandsynlighedsfordeling hælder til højre eller venstre, er skævheden dog lig med en anden værdi end nul, og værdien kvantificerer manglen på symmetri.
Kurtosis kvantificerer halernes tyngde i en fordeling. I en normalfordeling er kurtosis lig med nul. Den hale er den ting, som når ud til venstre eller højre. Men hvis en hale i en fordeling er tungere end en normalfordeling, er kurtosis et positivt tal. Hvis halerne i en fordeling er tyndere end i en normalfordeling, er kurtosis et negativt tal.
Sandsynligheder forvirrer ofte folk. En vigtig ting at forstå om konfidensniveauer er, at de er forbundet med fejlmarginen.
En anden vigtig ting at forstå om konfidensniveauer er, at jo større du gør din stikprøvestørrelse, jo mindre vil din fejlmargin bruge det samme konfidensniveau.
Som blot et eksempel kan du sige, at du havde nogle Google Analytics-data om to forskellige webannoncer, du kører for at promovere din lille virksomhed, og du vil vide, hvilken annonce der er mere effektiv. Du kan bruge konfidensintervalformlen til at finde ud af, hvor længe dine annoncer skal køre, før Google har indsamlet nok data til, at du kan vide, hvilken annonce der virkelig er bedre.
Sådan blokerer du Microsoft Word fra at åbne filer i skrivebeskyttet tilstand på Windows Microsoft Word åbner filer i skrivebeskyttet tilstand, hvilket gør det umuligt at redigere det? Bare rolig, metoderne er nedenfor
Sådan rettes fejl ved udskrivning af forkerte Microsoft Word-dokumenter Fejl ved udskrivning af Word-dokumenter med ændrede skrifttyper, rodede afsnit, manglende tekst eller tabt indhold er ret almindelige. Men lad være
Hvis du har brugt pennen eller highlighteren til at tegne på dine PowerPoint-dias under en præsentation, kan du gemme tegningerne til næste præsentation eller slette dem, så næste gang du viser den, starter du med rene PowerPoint-dias. Følg disse instruktioner for at slette pen- og highlighter-tegninger: Sletning af linjer en ved […]
Style-biblioteket indeholder CSS-filer, Extensible Stylesheet Language-filer (XSL) og billeder, der bruges af foruddefinerede mastersider, sidelayouts og kontrolelementer i SharePoint 2010. For at finde CSS-filer i Style-biblioteket på et udgivelsessted: Vælg Site Actions→ View Alt webstedsindhold. Indholdet af webstedet vises. Style-biblioteket ligger i […]
Overvæld ikke dit publikum med gigantiske tal. I Microsoft Excel kan du forbedre læsbarheden af dine dashboards og rapporter ved at formatere dine tal, så de vises i tusinder eller millioner.
Lær, hvordan du bruger SharePoints sociale netværksværktøjer, der lader enkeltpersoner og grupper kommunikere, samarbejde, dele og forbinde.
Julianske datoer bruges ofte i produktionsmiljøer som et tidsstempel og hurtig reference for et batchnummer. Denne type datokodning giver detailhandlere, forbrugere og serviceagenter mulighed for at identificere, hvornår et produkt blev fremstillet, og dermed produktets alder. Julianske datoer bruges også i programmering, militæret og astronomi. Forskellige […]
Du kan oprette en webapp i Access 2016. Så hvad er en webapp overhovedet? Nå, web betyder, at det er online, og app er kun en forkortelse for "applikation". En Custom Web App er en online databaseapplikation, der tilgås fra skyen ved hjælp af en browser. Du bygger og vedligeholder webappen i desktopversionen […]
De fleste sider i SharePoint 2010 viser en liste over navigationslinks på linjen Hurtig start langs venstre side af siden. Hurtig startlinjen viser links til fremhævet webstedsindhold såsom lister, biblioteker, websteder og udgivelsessider. Hurtigstartlinjen indeholder to meget vigtige links: Linket Alt webstedsindhold: […]
Ved simple problemer finder Solver i Excel som regel hurtigt de optimale Solver-variableværdier for objektivfunktionen. Men i nogle tilfælde har Solver problemer med at finde de Solver-variableværdier, der optimerer objektivfunktionen. I disse tilfælde viser Solver typisk en meddelelse eller en fejlmeddelelse, der beskriver eller diskuterer det problem, der […]
