Specialiųjų simbolių įterpimas į Word 2010
Kartais gali prireikti įterpti neįprastą simbolį į Word 2010 dokumentą. Perskaitykite, kaip lengvai tai padaryti su mūsų patarimais ir simbolių sąrašu.
Laikotarpių pasirinkimas naudojant „Excel“ pardavimo prognozę
Tarkime, kad jums reikia prognozuoti pardavimus laikotarpiui, kuris skiriasi nuo dabarties – pavyzdžiui, metams. Čia atsižvelgiama į sprendimą ir jūsų reikalavimų pobūdį.
Jei jūsų bazinę liniją sudaro keli metai, o faktiniai duomenys suskirstyti pagal mėnesius, vienas dalykas, kurį galite apsvarstyti, yra pakeisti bazinio laikotarpio laikotarpį iš mėnesių į metus. Tada galite prognozuoti visus kitus metus, nors jūsų prognozės nebūtų kas mėnesį. Gautumėte vieno žingsnio į priekį prognozę ir tas vienas žingsnis būtų visi metai.
Suvestinės lentelės yra naudingos apibendrinant pradinius duomenis ilgesniais laikotarpiais.
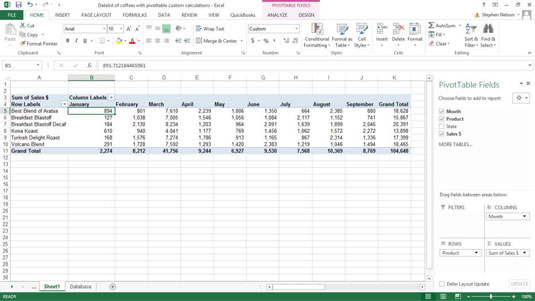
Štai kas vyksta paveikslėlyje:
- A stulpelyje nurodomas mėnuo, per kurį buvo pripažintos pajamos. Jis tęsiasi žemiau matomos darbalapio srities apačios iki 2016 m. gruodžio mėn.
- B stulpelyje pateikiamos kiekvieno mėnesio pajamos.
- Diapazone D3:E8 yra suvestinė lentelė. („Excel“ suvestinės lentelės yra didžiulis turtas, skirtas prognozuoti, o kaip jas naudoti, galite sužinoti 8 skyriuje.) Ši suvestinė lentelė paverčia A ir B stulpelių mėnesio duomenis į metinius duomenis – kiekvienų metų pajamų sumą.
- Kiekvienų metų prognozė, naudojant slankiuosius vidurkius, yra intervale G6:H8. Jūsų 2017 m. vieno žingsnio prognozė yra langelyje H9. Šiuo atveju prognozės pagrįstos dviejų metų slankiaisiais vidurkiais, o ne pasirodžiusiais trijų laikotarpių vidurkiais.
Šis metodas turi keletą trūkumų:
- Jūsų pradinis rodiklis svyruoja nuo 60 stebėjimų (mėnesinės pajamos per 5 metus, geras ilgas pradinis rodiklis) iki 5 stebėjimų (metinės pajamos per 5 metus, iš tikrųjų trumpa bazinė linija). Taip drastiškai sumažinus pradinės linijos ilgį, dažnai gaunami klaidinantys rezultatai. Tačiau kadangi mėnesinės pajamos auga taip pat laipsniškai kaip ir metinės bendros pajamos, galite šiek tiek pasitikėti metinėmis.
- Kas prašė prognozės – buhalteris, bankas, pardavimų vadybininkas, pardavimų viceprezidentas – galėjo kas mėnesį matyti 2017 metų prognozę. Jei taip, tikriausiai turėsite grįžti prie mėnesio pradinės linijos ir naudoti regresiją ( tikriausiai todėl , kad pradinėje linijoje galite rasti sezoniškumą, kuris palaikytų sezoninį išlyginimą).
Kaip naudoti logines funkcijas „Excel 2010“ formulėse
„Excel 2010“ naudoja septynias logines funkcijas – IR, FALSE, IF, IFERROR, NOT, OR ir TRUE. Sužinokite, kaip naudoti šias funkcijas efektyviai.
Kaip paslėpti ir rodyti eilutes ir stulpelius programoje „Excel 2016“.
Sužinokite, kaip paslėpti ir atskleisti stulpelius bei eilutes programoje „Excel 2016“. Šis patarimas padės sutaupyti laiko ir organizuoti savo darbalapius.
Kaip apskaičiuoti slenkančius vidurkius programoje „Excel“.
Išsamus vadovas, kaip apskaičiuoti slankiuosius vidurkius „Excel“ programoje, skirtas duomenų analizei ir orų prognozėms.
Kaip nukopijuoti formules naudojant automatinį pildymą programoje „Excel 2016“.
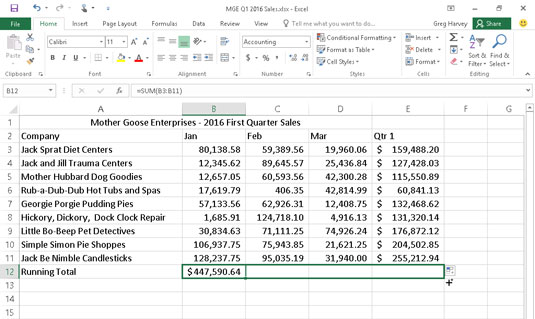
Sužinokite, kaip efektyviai nukopijuoti formules Excel 2016 programoje naudojant automatinio pildymo funkciją, kad pagreitintumėte darbo eigą.
Kaip „Excel 2010“ langeliams taikyti užpildymo spalvas, raštus ir gradientus
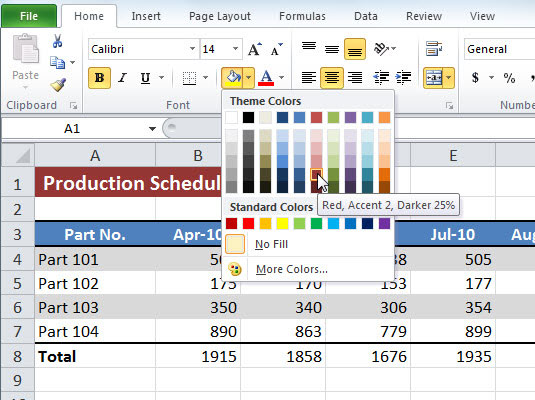
Galite pabrėžti pasirinktus langelius „Excel 2010“ darbalapyje pakeisdami užpildymo spalvą arba pritaikydami ląstelėms šabloną ar gradiento efektą.
Kaip paryškinti savaitgalio datas programoje „Excel“.
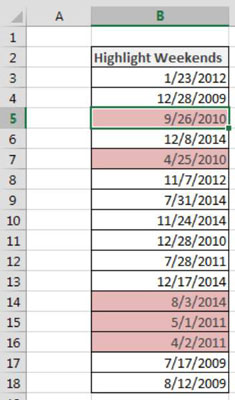
Dirbdami su laiko kortelėmis ir planuodami programą „Excel“, dažnai pravartu lengvai nustatyti bet kokias datas, kurios patenka į savaitgalius. Šiame straipsnyje pateikiami žingsniai, kaip naudoti sąlyginį formatavimą.
Kaip sukurti diagramas „Office 365“.
Sužinokite, kaip sukurti diagramas „Word“, „Excel“ ir „PowerPoint“ programose „Office 365“. Daugiau informacijos rasite LuckyTemplates.com.
Kaip sukurti pasirinktinius „Excel“ suvestinės lentelės skaičiavimus
„Excel“ suvestinės lentelės leidžia kurti <strong>pasirinktinius skaičiavimus</strong>, įtraukiant daug pusiau standartinių skaičiavimų. Šiame straipsnyje pateiksiu detalius nurodymus, kaip efektyviai naudoti šią funkciją.
Kaip pakeisti rašybos tikrinimo ir gramatikos nustatymus programoje „Word 2016“.
Nesvarbu, ar dievinate, ar nekenčiate Word gebėjimo išjuokti jūsų kalbos gebėjimus, jūs turite galutinį sprendimą. Yra daug nustatymų ir parinkčių, leidžiančių valdyti „Word“ rašybos ir gramatikos tikrinimo įrankius.