A Pi egy alapvető matematikai állandó, amely a kör kerületének és átmérőjének arányát jelenti. A Pi kihasználása a Pythonban alapvető fontosságú geometriai számítások, trigonometria és számos egyéb matematikai művelet során.
A Pi (π) a kör kerületének (c) és átmérőjének (d) arányát jelenti, ahol ? = c/d. A pi értéke körülbelül 3,14159, és irracionális szám, ami azt jelenti, hogy végtelenségig folytatódik, anélkül, hogy ismételné önmagát.
Íme a pi első néhány számjegye:
3.14159265358979323846...
A pi-hez való hozzáférés négy leggyakoribb módja a Pythonban:
Ne feledje, hogy a Python math.pi állandója a legtöbb célra elég pontos, azonban más könyvtárakon keresztül még ennél is pontosabb közelítések érhetők el. A megfelelő könyvtár kiválasztása az Ön igényeitől és a szükséges funkcióktól függ.
A Python matematikai modulja lehetővé teszi a pi számmal való munkát, és akár 15 tizedesjegyig pontos közelítést ad. Két lehetősége van a pi importálására:
Például:
import math
pi_value = math.pifrom math import pi
pi_value = piA pi állandón kívül a matematikai modul számos más matematikai függvényt is kínál. Ezek kombinálhatók math.pi-val, hogy:
A kör kerülete a következő képlettel számítható ki:
C = 2 ? r (C - kerület, ? - Pi állandó, r - sugár)
Példa a kódra:
import math
radius = 5
circumference = 2 * math.pi * radius
print(circumference)
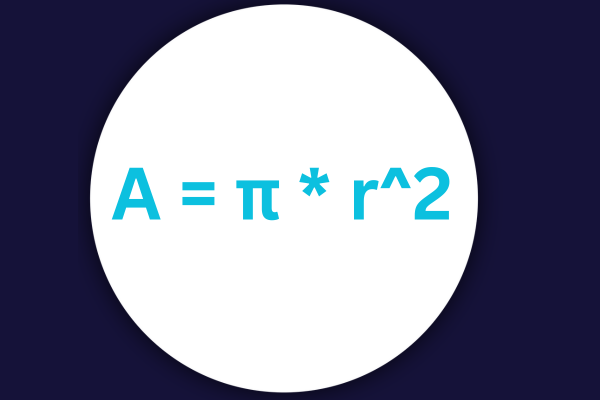
A kör területe a következőképpen számítható ki:
A = ? * r^2
Példa a kódra:
import math
radius = 5
area = math.pi * (radius ** 2)
print(area)
A szögeket fokban és radiánban mérik. A fokok radiánra konvertálásához használja a következő képletet:
Radián = fok * (? / 180) vagy a math.radians() függvényt.
Példa:
import math
angle_degrees = 45
angle_radians = math.radians(angle_degrees)
print(angle_radians)A NumPy egy népszerű Python-könyvtár, amely számadatokkal dolgozik. Az alábbiakban található a telepítési és importálási példa:
pip install numpy
import numpy as np
pi_value = np.pi
print(pi_value)A SciPy egy másik széles körben használt Python-könyvtár, amely a NumPy könyvtárra épül:
pip install scipy
import scipy
pi_value = scipy.pi
print(pi_value)A Python támogatja a komplex számokat a cmath modulon keresztül:
import cmath
z = 1 + 1j
result = cmath.exp(z * cmath.pi)
print(result) # Output: (-1-2.8421709430404007e-14j)
Számítási hibák esetén érdemes a következő kivételkezelési technikákat alkalmazni:
Példa a hibakezelésre:
try:
# Perform calculation here
except (ZeroDivisionError, OverflowError, ArithmeticError):
# Handle specific errors here
finally:
# Code to be executed regardless of any exceptionsMegtanulta, hogyan érheti el a Pi-t négy különböző Python-modul használatával. Igényeitől függően mindenképp azt válassza, amelyik biztosítja a szükséges pontosságot.
Ha további segítségre van szüksége, keresse fel közösségünket és nagyszerű forrásainkat. Boldog kódolást!
Ebből a blogból megtudhatja, hogyan mentheti automatikusan az e-mail mellékleteket a SharePointba, majd törölheti az e-maileket a Power Automate segítségével.
A Microsoft LuckyTemplates irányítópult 18 legjobb példája 2023
Ismerje meg, hogyan hozhat létre <strong>Power Automate</strong> folyamatokat a semmiből. Sablon használata helyett mi magunk hozzuk létre a kiváltó okokat és a műveleteket.
4 módszer a Pi használatára a Pythonban példákkal
Ebben az útmutatóban bemutatom, hogyan lehet Pénzügyi információk mátrixát létrehozni a Profit és veszteség (P&L) kimutatással a LuckyTemplates alkalmazásban.
Fedezze fel, hogyan lehet dinamikusan egyesíteni oszlopokat a Power Query Table.CombineColumns függvény segítségével.
Ismerje meg, hogyan adhatjuk hozzá és szinkronizálhatjuk SharePoint-fájljainkat az asztalon és a OneDrive-on.
Tudja meg, miért fontos egy dedikált dátumtáblázat a LuckyTemplatesben, és ismerje meg ennek leggyorsabb és leghatékonyabb módját.
Ez a rövid oktatóanyag kiemeli a LuckyTemplates mobil jelentési funkcióját. Megmutatom, hogyan készíthet hatékony jelentéseket mobileszközökön.
Ebben a LuckyTemplates bemutatóban olyan jelentéseket tekintünk át, amelyek professzionális szolgáltatáselemzést mutatnak be egy olyan cégtől, amely több szerződéssel és ügyfél-elkötelezettséggel rendelkezik.
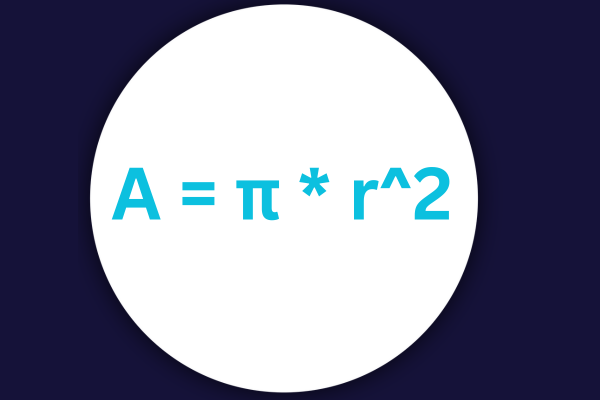
András Tóth -
Ó, imádom a Pi-t és a Python-t! Nagyon jól megírt cikk, köszönet érte! A harmadik módszert mindenképpen ki fogom próbálni egy projektre. A végén sokat lehet tanulni belőle
Mia 88 -
Kiváló írás, csupán egy dolgot hiányolok: Mi lenne, ha a jövőben a Pi és a webfejlesztés kapcsolatáról is írnátok? Az izgalmas lenne, ha tudnám, hogy lehet a Pi-t webes környezetben használni
Péter IT -
Szuper cikk! Az első módszer különösen tetszik, mert egyszerű és hatékony. Használható, amikor a Pi-t beépített alkalmazások készítésére használom. Milyen más projekteket javasoltok, ahol a Pi-t alkalmazhatom
Gábor -
Köszönöm a cikket! Nagyon hasznosnak találom a Python és a Pi kapcsolatáról szóló információkat. A második módszert próbálom ki, és alig várom, hogy lássam az eredményt
Eva K. -
Köszönöm szépen, hogy megosztottad a tudásodat! A Pi érdekes egy kis gép, és a Python valóban tökéletes a használatához. Mindenki, aki érdeklődik a technológia iránt, próbálja ki ezt a párost!
Kata Mókus -
Ez igazán érdekes! Én eddig csak a harmadik módszert használtam, de most kipróbálom az elsőt is. Lehet, hogy a vizuális munka segít jobban megérteni a Pi használatát
Szilvia -
Egy kérdésem van: van esetleg tapasztalatotok a Pi 4 használatával? Én eddig csak a Pi 3-t használtam. Készítettem egy projektet a zaj csökkentésére, és kíváncsi lennék, hogyan változna a teljesítmény
Hanna -
A második módszerről érdekes tapasztalataim lettek. Miközben dolgoztam rajta, rájöttem, hogy sokkal kreatívabban tudok gondolkodni a Python és a Pi együttműködéséről. Köszönöm a kezdő lépéseket!
László 23 -
Fantasztikus írás! Jól van megfogalmazva, és könnyen követhető. A folyamatok leírása segített, hogy jobban megértsem, hogyan működik a Pi Pythonban. Kíváncsi vagyok, lesz-e folytatás!