Змініть формати дати за допомогою редактора Power Query
У цьому посібнику ви дізнаєтеся, як перетворити текст у формат дати за допомогою редактора Power Query в LuckyTemplates.
Якщо ви працювали з Python для аналізу даних або машинного навчання, ви, ймовірно, стикалися з масивами NumPy. Вони є потужним інструментом для роботи з числовими даними, але іноді дані в цих масивах потрібно скоригувати або «нормалізувати», щоб ефективно використовувати їх у ваших алгоритмах. Але що означає нормалізувати масив?
Щоб нормалізувати масив NumPy, вам потрібно налаштувати значення в масиві так, щоб вони потрапляли в певний діапазон, зазвичай між 0 і 1, або щоб вони мали стандартний нормальний розподіл із середнім значенням 0 і стандартним відхиленням 1. Це часто робиться в області машинного навчання та аналізу даних, щоб гарантувати, що всі вхідні функції мають однаковий масштаб.

У цій статті ми розглянемо, як можна нормалізувати масив NumPy у Python. Ми розглянемо різні методи, які можна використовувати для нормалізації масиву NumPy, а також розглянемо приклади, які допоможуть вам краще зрозуміти концепцію.
Давайте потрапимо в це!
Зміст
Які основи нормалізації в Python?
Перш ніж запровадити нормалізацію в Python, ви повинні зрозуміти, що означає нормалізація.

Тому в цьому розділі ми розглянемо, що таке нормалізація та її основні поняття.
Що таке нормалізація?
Нормалізація — це процес масштабування та перетворення даних у стандартизований діапазон. Це робиться шляхом ділення кожного елемента даних на параметр. Параметр може бути максимальним значенням, діапазоном або іншою нормою.
Ви можете нормалізувати масив NumPy за допомогою евклідової норми (також відомої як норма L2). Крім того, ви також можете нормалізувати масиви NumPy, змінивши значення в певному діапазоні, зазвичай від 0 до 1.
У Python бібліотека NumPy забезпечує ефективний спосіб нормалізації масивів. Це також включає багатовимірні масиви та матриці.
Чому нормалізація важлива?
Нормалізація важлива, оскільки вона забезпечує однакову обробку різних функцій під час порівняння та аналізу даних. Ви можете використовувати його для усунення потенційних упереджень або розбіжностей, які можуть виникнути через різні масштаби.
Що таке норми?
Параметр, який ви використовуєте для нормалізації, може бути різними нормами , такими як Евклідова норма (L2), Манхеттенська норма (L1) або максимальна норма (L_inf). Ви використовуєте норми для обчислення величини вектора або матриці . Потім вони використовуються як коефіцієнт масштабування для нормалізації даних.
Під час роботи з матрицями ми часто використовуємо норму Фробеніуса , яка є узагальненням евклідової норми для багатовимірних масивів.
У наступному прикладі показано нормалізацію матриці за допомогою норми Фробеніуса:
import numpy as np
# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
# Calculate the Frobenius norm
frobenius_norm = np.linalg.norm(matrix, 'fro')
# Normalize the matrix
normalized_matrix = matrix / frobenius_norm
print('Original Matrix:')
print(matrix)
print('nFrobenius Norm:')
print(frobenius_norm)
print('nNormalized Matrix:')
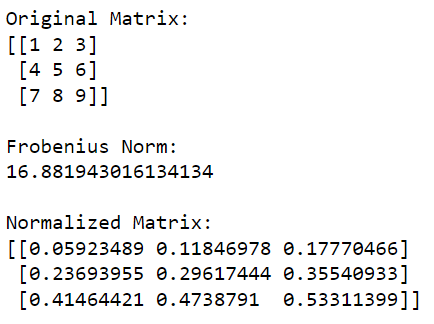
print(normalized_matrix)Цей код Python спочатку імпортує бібліотеку NumPy і використовує її для створення матриці. Потім він обчислює норму Фробеніуса матриці, а потім ділить кожен елемент у матриці на це значення, щоб нормалізувати його.
Результат цього коду наведено нижче:
Що таке нормалізація в машинному навчанні?
У машинному навчанні нормалізація є важливим етапом попередньої обробки, оскільки вона покращує продуктивність алгоритмів.
Виконуючи методи оптимізації на основі градієнта, ви побачите, що оптимізовані функції, як правило, зближуються швидше та ефективніше. Це тому, що це зменшує ризик поганого масштабування або зникнення градієнтів.
Які є методи нормалізації в Python?
Нормалізацію масивів можна виконати декількома способами. Однак одні методи більш популярні, ніж інші, завдяки своїй високій ефективності.
У цьому розділі ми розглянемо три широко використовувані методи нормалізації:
Мінімально-максимальне масштабування
Нормалізація L1
Нормалізація L2
1. Як виконати мінімально-максимальне масштабування
Мін.-макс. масштабування також відоме як лінійна нормалізація або масштабування ознак. При мінімально-максимальному масштабуванні ми масштабуємо значення масиву NumPy таким чином, щоб вони потрапляли в заданий діапазон, як правило, від 0 до 1.
Для цього ви віднімаєте мінімальне значення від кожного елемента та ділите результат на різницю між максимальним і мінімальним значеннями.
Ви можете представити мінімально-максимальне масштабування математично як:
x' = (x - min(x)) / (max(x) - min(x))У наведеному нижче прикладі показано, як можна виконувати мінімально-максимальне масштабування за допомогою бібліотеки NumPy:
import numpy as np
# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
# Perform min-max scaling
min_val = np.min(matrix)
max_val = np.max(matrix)
scaled_matrix = (matrix - min_val) / (max_val - min_val)
print('Original Matrix:')
print(matrix)
print('nMin-Max Scaled Matrix:')
print(scaled_matrix)Цей код спочатку імпортує NumPy, а потім обчислює мінімальне та максимальне значення в матриці, яку потім масштабує таким чином, щоб усі значення були між 0 (що відповідає початковому мінімальному значенню) та 1 (що відповідає початковому максимальному значенню).
Результат цього коду наведено нижче:

Мінімально-максимальне масштабування є дуже поширеною формою масштабування в машинному навчанні та попередній обробці даних.
2. Як виконати нормалізацію L1
Нормалізація L1 використовує L1-норму, яка є сумою абсолютних значень елементів масиву. Це особливо корисно для розріджених матриць. Він гарантує, що сума абсолютних значень нормалізованих елементів масиву дорівнює 1.
Формула для нормалізації L1:
x' = x / sum(|x|)У наступному прикладі показано, як можна виконати нормалізацію L1 за допомогою NumPy:
import numpy as np
# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
# Perform L1 normalization
l1_norm = np.linalg.norm(matrix, 1, axis=1, keepdims=True)
l1_normalized_matrix = matrix / l1_norm
print('Original Matrix:')
print(matrix)
print('nL1 Normalized Matrix:')
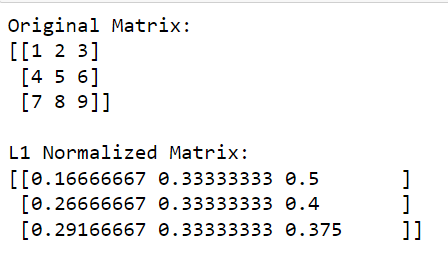
print(l1_normalized_matrix)У цьому коді np.linalg.norm (matrix, 1, axis=1, keepdims=True) обчислює норму L1 для кожного рядка (це робиться шляхом вказівки axis=1).
Ця операція поверне вектор-стовпець, де кожен елемент є нормою L1 відповідного рядка. Розділивши вихідну матрицю на ці норми (виконуючи ділення поелементно), ми отримаємо L1 нормалізовану версію матриці.
Результат наведено нижче:
3. Як виконати нормалізацію L2
Нормалізація L2 використовує L2-норму, яка є квадратним коренем із суми квадратів елементів масиву.
Цей метод перетворює нормалізований масив на одиничний вектор із 2-нормою 1. Нормалізація L2 корисна для зменшення розмірів і забезпечує однакову важливість для всіх функцій.
Формула нормалізації L2:
x' = x / sqrt(sum(x^2))Ось як ви можете виконати нормалізацію L2 за допомогою NumPy :
import numpy as np
# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
# Perform L2 normalization
l2_norm = np.linalg.norm(matrix, 2, axis=1, keepdims=True)
l2_normalized_matrix = matrix / l2_norm
print('Original Matrix:')
print(matrix)
print('nL2 Normalized Matrix:')
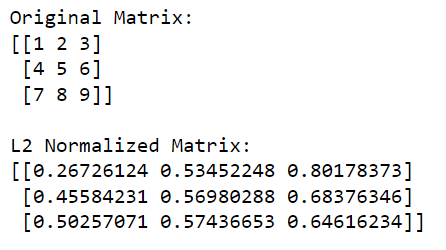
print(l2_normalized_matrix)У цьому коді np.linalg.norm(matrix, 2, axis=1, keepdims=True) обчислює норму L2 (евклідову норму) для кожного рядка (це робиться шляхом вказівки axis=1). Ця операція поверне вектор-стовпець, де кожен елемент є нормою L2 відповідного рядка.
Розділивши вихідну матрицю на ці норми (виконуючи поелементний ділення), ми отримаємо L2 нормалізовану версію матриці.
Результат наведено нижче:
Гаразд, тепер, коли ми розглянули популярні способи створення нормалізованого масиву за допомогою NumPy, давайте подивимося, як можна зробити те саме за допомогою інших бібліотек Python у наступному розділі.
Як використовувати Scikit-Learn для нормалізації в Python
Scikit-learn — потужна бібліотека Python для машинного навчання. Він надає кілька інструментів для попередньої обробки даних.
Одним із інструментів, яким ви можете скористатися, є модуль sklearn.preprocessing , який пропонує різноманітні методи нормалізації. Доступно багато різних функцій масштабування, трансформаторів і нормалізаторів. Однак ми зосередимося на MinMaxScaler і normalize .
Для попередньої обробки даних за допомогою scikit-learn ви переважно використовуєте transformer API. Це включає методи fit , transform і fit_transform .
1. Як нормалізувати масив за допомогою MinMaxScaler
MinMaxScaler — це засіб масштабування, який нормалізує дані до заданого діапазону, зазвичай [0, 1] .
Формула MinMaxScalar наведена нижче:
scaled_value = (value - min_value) / (max_value - min_value)Щоб реалізувати MinMaxScaler , виконайте такі дії:
Імпортуйте необхідні бібліотеки:
import numpy as np
from sklearn.preprocessing import MinMaxScalerСтворіть масив NumPy:
data = np.array([[1., 2., 5.], [3., 6., 8.], [5., 10., 12.]])Створіть екземпляр MinMaxScaler і підберіть його до даних:
scaler = MinMaxScaler()
scaler.fit(data)Перетворіть дані за допомогою методу transform або fit_transform :
normalized_data = scaler.transform(data)Результат цього коду наведено нижче:

Як ви бачите у вихідних даних, MinMaxScalarMatrix має лише значення в діапазоні від 0 до 1.
2. Як виконати нормалізацію рядків на місці
Ви також можете використовувати нормалізацію рядка на місці як альтернативу, використовуючи функцію normalize .
Цей метод нормалізує кожен вхідний масив або функцію незалежно шляхом масштабування вектора до одиничної норми. За замовчуванням функція нормалізації використовує норму L2 для виконання простої нормалізації, але ви можете вибрати інші параметри норми.
Наступний приклад демонструє нормалізацію рядка на місці:
from sklearn.preprocessing import normalize
import numpy as np
# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]], dtype=float)
# Apply in-place row normalization
normalize(matrix, norm='l2', copy=False)
print('L2 Normalized Matrix:')
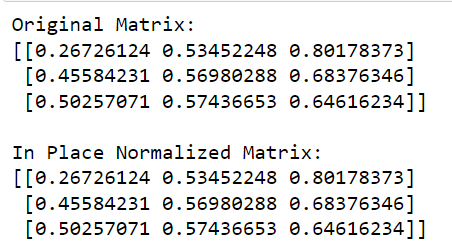
print(matrix)У цьому коді ми викликаємо функцію нормалізації з sklearn , визначаємо норму для використання ('l2' у цьому випадку) і встановлюємо copy=False для виконання нормалізації на місці.
Результат цього коду наведено нижче:
Щоб дізнатися більше про машинне навчання в , перегляньте це відео:
Заключні думки
Досліджуючи науку про дані та машинне навчання, ви побачите, що процес нормалізації є важливим кроком у вашому конвеєрі попередньої обробки даних.
По-перше, він розміщує різні характеристики на загальній шкалі. Це робить ваші моделі менш чутливими до масштабу вхідних даних. Це може значно покращити продуктивність багатьох алгоритмів машинного навчання.
По-друге, це допоможе вам прискорити процес навчання. Деякі алгоритми, особливо ті, що базуються на обчисленні обчислень відстані, збігаються швидше, коли дані нормалізуються.
Навчившись нормалізувати дані, ви отримаєте важливу навичку. Нормалізація — це практичний інструмент, який регулярно використовується в реальних програмах. Це допоможе вам зменшити ймовірність отримання неочікуваних результатів через викиди або різницю в одиницях.
Як і будь-який інструмент, ключ до оволодіння нормалізацією лежить на практиці. Тож не соромтеся забруднити руки та експериментувати з різними наборами даних і випадковими значеннями. Світ вашої устриці. Щасливого кодування!
У цьому посібнику ви дізнаєтеся, як перетворити текст у формат дати за допомогою редактора Power Query в LuckyTemplates.
Дізнайтеся, як об’єднати файли з кількох папок у мережі, робочому столі, OneDrive або SharePoint за допомогою Power Query.
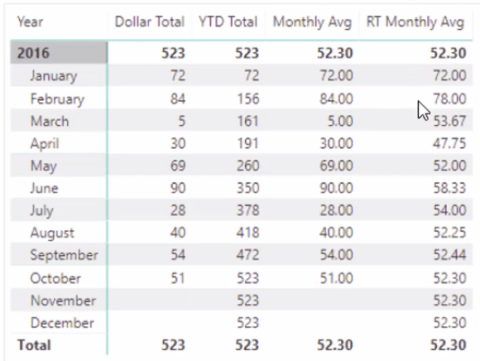
Цей підручник пояснює, як обчислити місячне ковзне середнє на базі даних з початку року за допомогою функцій AVERAGEX, TOTALYTD та FILTER у LuckyTemplates.
Дізнайтеся, чому важлива спеціальна таблиця дат у LuckyTemplates, і вивчіть найшвидший і найефективніший спосіб це зробити.
У цьому короткому посібнику розповідається про функцію мобільних звітів LuckyTemplates. Я збираюся показати вам, як ви можете ефективно створювати звіти для мобільних пристроїв.
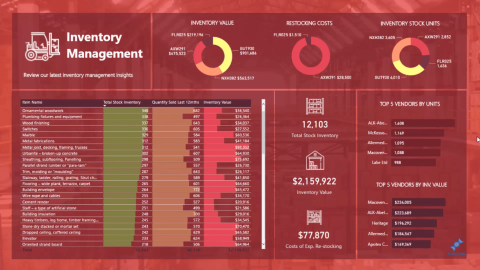
У цій презентації LuckyTemplates ми розглянемо звіти, що демонструють професійну аналітику послуг від фірми, яка має кілька контрактів і залучених клієнтів.
Ознайомтеся з основними оновленнями для Power Apps і Power Automate, а також їх перевагами та наслідками для Microsoft Power Platform.
Відкрийте для себе деякі поширені функції SQL, які ми можемо використовувати, наприклад String, Date і деякі розширені функції для обробки та маніпулювання даними.
У цьому підручнику ви дізнаєтеся, як створити свій ідеальний шаблон LuckyTemplates, налаштований відповідно до ваших потреб і вподобань.
У цьому блозі ми продемонструємо, як шарувати параметри поля з малими кратними, щоб створити неймовірно корисну інформацію та візуальні ефекти.