Vad är matrisformler i Excel 2013?

En matrisformel i Excel 2013 (och andra kalkylblad) är en speciell formel som fungerar på ett antal värden. Om ett cellområde tillhandahåller detta område (som ofta är fallet) kallas det för ett arrayområde . Om detta intervall tillhandahålls av en lista med numeriska värden kallas de för en matriskonstant .

Många kalkylbladstabeller använder en originalformel som du kopierar till intilliggande celler genom att använda relativa cellreferenser (kallas ibland för en kopia av en till många ). I vissa fall kan du bygga den ursprungliga formeln så att Excel utför den önskade beräkningen inte bara i den aktiva cellen, utan även i alla andra celler som du normalt skulle kopiera formeln till. Du gör detta genom att skapa en matrisformel .

Även om arraykonceptet kan verka främmande till en början, är du egentligen ganska bekant med arrayer eftersom kolumn-och-radstrukturen i Excel-kalkylbladets rutnät naturligt organiserar dina dataområden i endimensionella och tvådimensionella arrayer. (1-D-matriser tar upp en enda rad eller kolumn, medan 2-D-matriser tar upp flera rader och kolumner.)

Följande figur illustrerar ett par tvådimensionella arrayer med numeriska poster av två olika storlekar. Den första arrayen är en 3 x 2 array i cellområdet B2:C4. Denna array är en 3 x 2 array eftersom den upptar tre rader och två kolumner.

Den andra arrayen är en 2 x 3 array i cellområdet F2:H3. Denna array är en 2 x 3 array eftersom den använder två rader och tre kolumner.

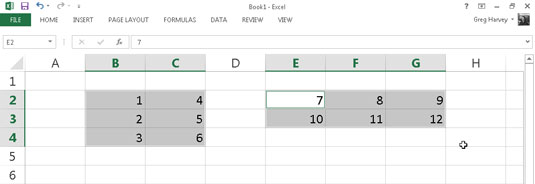
Om du skulle lista värdena i den första 3 x 2-matrisen som en matriskonstant i en formel, skulle de se ut enligt följande:

{1,4;2,5;3,6}

Flera saker i denna lista är anmärkningsvärda. Först är arraykonstanten innesluten i ett par klammerparenteser ({}). För det andra är kolumner inom varje rad separerade med kommatecken (,) och rader inom arrayen separeras med semikolon (;). För det tredje listas konstanterna i arrayen över varje rad och sedan ner i varje kolumn och inte ner i varje kolumn och över varje rad.

Den andra 2 x 3-matrisen uttryckt som en matriskonstant ser ut som följer:

{7,8,9;10,11,12}

Notera igen att du listar värdena över varje rad och sedan ner i varje kolumn, och separerar värdena i olika kolumner med kommatecken och värdena i olika rader med semikolon.

Användningen av matrisformler kan avsevärt minska mängden formelkopiering som du måste göra i ett kalkylblad genom att producera flera resultat över hela matrisområdet i en enda operation.

Dessutom använder matrisformler mindre datorminne än standardformler som kopieras i ett intervall. Detta kan vara viktigt när du skapar ett stort kalkylblad med många tabeller eftersom det kan betyda skillnaden mellan att passa in alla dina beräkningar på ett kalkylblad och att behöva dela upp din modell i flera kalkylbladsfiler.