För att hjälpa dig förstå statistisk analys med Excel, hjälper det att simulera Central Limit Theorem. Det låter nästan inte rätt. Hur kan en population som inte är normalfördelad resultera i en normalfördelad urvalsfördelning?
För att ge dig en uppfattning om hur Central Limit Theorem fungerar finns det en simulering. Denna simulering skapar något som liknar en samplingsfördelning av medelvärdet för ett mycket litet urval, baserat på en population som inte är normalfördelad. Som du kommer att se, även om populationen inte är en normalfördelning, och även om urvalet är litet, ser urvalsfördelningen av medelvärdet ganska ut som en normalfördelning.
Föreställ dig en enorm population som består av bara tre poäng - 1, 2 och 3 - och var och en är lika sannolikt att visas i ett urval. Föreställ dig också att du kan slumpmässigt välja ett urval av tre poäng från denna population.
Alla möjliga prov av tre poäng (och deras medel) från en population som består av poängen 1, 2 och 3
| Prov | Betyda | Prov | Betyda | Prov | Betyda |
| 1,1,1 | 1.00 | 2,1,1 | 1,33 | 3,1,1 | 1,67 |
| 1,1,2 | 1,33 | 2,1,2 | 1,67 | 3,1,2 | 2.00 |
| 1,1,3 | 1,67 | 2,1,3 | 2.00 | 3,1,3 | 2,33 |
| 1,2,1 | 1,33 | 2,2,1 | 1,67 | 3,2,1 | 2.00 |
| 1,2,2 | 1,67 | 2,2,2 | 2.00 | 3,2,2 | 2,33 |
| 1,2,3 | 2.00 | 2,2,3 | 2,33 | 3,2,3 | 2,67 |
| 1,3,1 | 1,67 | 2,3,1 | 2.00 | 3,3,1 | 2,33 |
| 1,3,2 | 2.00 | 2,3,2 | 2,33 | 3,3,2 | 2,67 |
| 1,3,3 | 2,33 | 2,3,3 | 2,67 | 3,3,3 | 3.00 |
Om du tittar noga på tabellen kan du nästan se vad som är på väg att hända i simuleringen. Det urvalsmedelvärde som förekommer oftast är 2,00. De urvalsmedel som förekommer minst frekvent är 1,00 och 3,00. Hmmm. . . .
I simuleringen valdes en poäng slumpmässigt ut från populationen och sedan slumpmässigt två till. Den gruppen med tre poäng är ett exempel. Sedan beräknar du medelvärdet av det provet. Denna process upprepades för totalt 60 prover, vilket resulterade i 60 provmedelvärden. Slutligen ritar du en graf över fördelningen av urvalsmedlen.
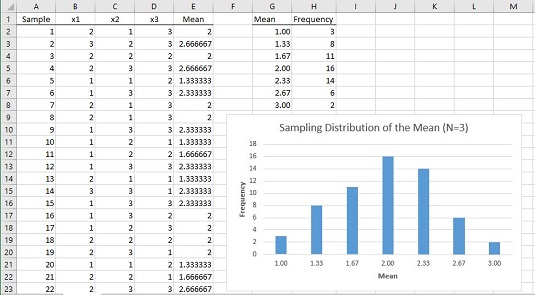
Hur ser den simulerade samplingsfördelningen av medelvärdet ut? Bilden nedan visar ett arbetsblad som besvarar denna fråga.
I kalkylbladet är varje rad ett exempel. Kolumnerna märkta x1, x2 och x3 visar de tre poängen för varje prov. Kolumn E visar medelvärdet för provet i varje rad. Kolumn G visar alla möjliga värden för provmedelvärdet, och kolumn H visar hur ofta varje medelvärde förekommer i de 60 proven. Kolumnerna G och H, och grafen, visar att fördelningen har sin maximala frekvens när urvalsmedelvärdet är 2,00. Frekvenserna avtar när samplingsmedlen kommer längre och längre bort från 2.00.
Poängen med allt detta är att populationen inte ser ut som en normalfördelning och urvalsstorleken är mycket liten. Även under dessa begränsningar börjar provtagningsfördelningen av medelvärdet baserat på 60 prover att likna en normalfördelning.
Hur är det med parametrarna som Central Limit Theorem förutsäger för samplingsfördelningen? Börja med befolkningen. Populationsmedelvärdet är 2,00 och populationens standardavvikelse är 0,67. (Denna typ av population kräver lite snygg matematik för att ta reda på parametrarna.)
Till provfördelningen. Medelvärdet för de 60 medelvärdena är 1,98 och deras standardavvikelse (en uppskattning av medelvärdets standardfel) är 0,48. Dessa siffror är nära de förutsagda parametrarna för Central Limit Theorem för provtagningsfördelningen av medelvärdet, 2,00 (lika med populationsmedelvärdet) och 0,47 (standardavvikelsen, 0,67, dividerat med kvadratroten ur 3, urvalsstorleken) .
Om du är intresserad av att göra denna simulering, här är stegen:
Välj en cell för ditt första slumpmässigt valda nummer.
Välj cell B2.
Använd kalkylbladsfunktionen RANDBETWEEN för att välja 1, 2 eller 3.
Detta simulerar att du ritar ett tal från en population som består av siffrorna 1, 2 och 3 där du har lika stor chans att välja varje nummer. Du kan antingen välja FORMLER | Math & Trig | RANDBETWEEN och använd dialogrutan Funktionsargument eller skriv bara =RANDBETWEEN(1,3) i B2 och tryck på Enter. Det första argumentet är det minsta talet RANDBETWEEN returnerar, och det andra argumentet är det största talet.
Välj cellen till höger om den ursprungliga cellen och välj ett annat slumptal mellan 1 och 3. Gör detta igen för ett tredje slumptal i cellen till höger om den andra.
Det enklaste sättet att göra detta är att autofylla de två cellerna till höger om den ursprungliga cellen. I det här arbetsbladet är dessa två celler C2 och D2.
Betrakta dessa tre celler som ett prov och beräkna deras medelvärde i cellen till höger om den tredje cellen.
Det enklaste sättet att göra detta är att bara skriva =AVERAGE(B2:D2) i cell E2 och trycka på Enter.
Upprepa denna process för så många prover som du vill inkludera i simuleringen. Låt varje rad motsvara ett prov.
60 prover användes här. Det snabba och enkla sättet att få detta gjort är att välja den första raden av tre slumpmässigt valda nummer och deras medelvärde och sedan autofylla de återstående raderna. Uppsättningen av provmedelvärden i kolumn E är den simulerade provtagningsfördelningen av medelvärdet. Använd AVERAGE och STDEV.P för att hitta dess medelvärde och standardavvikelse.
För att se hur den här simulerade samplingsfördelningen ser ut, använd arrayfunktionen FREQUENCY på sampelmedelvärdet i kolumn E. Följ dessa steg:
Ange de möjliga värdena för provmedelvärdet i en matris.
Du kan använda kolumn G för detta. Du kan uttrycka de möjliga värdena för provmedelvärdet i bråkform (3/3, 4/3, 5/3, 6/3, 7/3, 8/3 och 9/3) som de som anges i cellerna G2 till G8. Excel konverterar dem till decimalform. Se till att dessa celler är i nummerformat.
Välj en matris för frekvenserna för de möjliga värdena för provmedelvärdet.
Du kan använda kolumn H för att hålla frekvenserna och markera cellerna H2 till H8.
Från menyn Statistiska funktioner, välj FREKVENS för att öppna dialogrutan Funktionsargument för FREKVENS
I dialogrutan Funktionsargument anger du lämpliga värden för argumenten.
I rutan Data_array anger du cellerna som innehåller provmedelvärdet. I det här exemplet är det E2:E61.
Identifiera den matris som innehåller de möjliga värdena för provmedelvärdet.
FREQUENCY håller denna array i rutan Bins_array. För detta kalkylblad går G2:G8 in i rutan Bins_array. När du har identifierat båda arrayerna visar dialogrutan Funktionsargument frekvenserna inom ett par krulliga parenteser.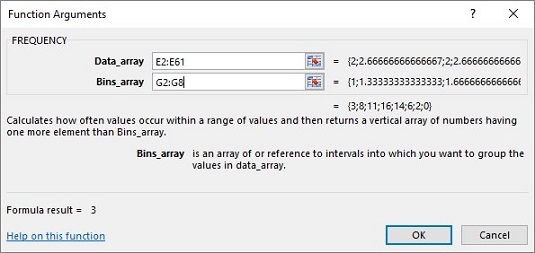
Tryck på Ctrl+Skift+Enter för att stänga dialogrutan Funktionsargument och visa frekvenserna.
Använd denna tangentkombination eftersom FREQUENCY är en arrayfunktion.
Slutligen, med H2:H8 markerad, välj Infoga | Rekommenderade diagram och välj layouten Clustered Column för att skapa grafen över frekvenserna. Din graf kommer förmodligen att se något annorlunda ut än min, eftersom du sannolikt kommer att sluta med ett annat slumptal.
Förresten, Excel upprepar den slumpmässiga urvalsprocessen när du gör något som får Excel att räkna om kalkylbladet. Effekten är att siffrorna kan ändras när du arbetar igenom detta. (Det vill säga att du kör simuleringen igen.) Om du till exempel går tillbaka och autofyller en av raderna igen, ändras siffrorna och grafen ändras.
Lär dig att använda kommandona Gör om och Upprepa i Word 2016 för att effektivt hantera dina dokument. Dessa funktioner hjälper dig att enkelt ångra och återställa ändringar.
Hur man blockerar Microsoft Word från att öppna filer i skrivskyddat läge på Windows Microsoft Word öppnar filer i skrivskyddat läge, vilket gör det omöjligt att redigera dem? Oroa dig inte, metoderna finns nedan
Så här åtgärdar du fel vid utskrift av felaktiga Microsoft Word-dokument Fel vid utskrift av Word-dokument med ändrade teckensnitt, röriga stycken, saknad text eller förlorat innehåll är ganska vanligt. Men gör det inte
Om du har använt pennan eller överstrykningspennan för att rita på dina PowerPoint-bilder under en presentation, kan du spara ritningarna till nästa presentation eller radera dem så att nästa gång du visar den börjar du med rena PowerPoint-bilder. Följ dessa instruktioner för att radera ritningar med penna och överstrykningspenna: Radera linjer ett på […]
Stilbiblioteket innehåller CSS-filer, XSL-filer (Extensible Stylesheet Language) och bilder som används av fördefinierade mallsidor, sidlayouter och kontroller i SharePoint 2010. För att hitta CSS-filer i stilbiblioteket på en publiceringswebbplats: Välj Webbplatsåtgärder→Visa Allt webbplatsinnehåll. Innehållet på webbplatsen visas. Style-biblioteket ligger i […]
Överväldiga inte din publik med gigantiska siffror. I Microsoft Excel kan du förbättra läsbarheten för dina instrumentpaneler och rapporter genom att formatera dina siffror så att de visas i tusentals eller miljoner.
Lär dig hur du använder SharePoints sociala nätverksverktyg som låter individer och grupper kommunicera, samarbeta, dela och ansluta.
Julianska datum används ofta i tillverkningsmiljöer som en tidsstämpel och snabbreferens för ett batchnummer. Denna typ av datumkodning tillåter återförsäljare, konsumenter och serviceagenter att identifiera när en produkt tillverkades och därmed produktens ålder. Julianska datum används också i programmering, militären och astronomi. Annorlunda […]
Du kan skapa en webbapp i Access 2016. Så vad är en webbapp egentligen? Tja, webben betyder att den är online, och appen är bara en förkortning för "applikation". En anpassad webbapp är en onlinedatabasapplikation som nås från molnet med en webbläsare. Du bygger och underhåller webbappen i skrivbordsversionen […]
De flesta sidor i SharePoint 2010 visar en lista med navigeringslänkar i snabbstartsfältet till vänster på sidan. Snabbstartsfältet visar länkar till utvalt webbplatsinnehåll som listor, bibliotek, webbplatser och publiceringssidor. Snabbstartsfältet innehåller två mycket viktiga länkar: Länken Allt webbplatsinnehåll: […]
