Funktionerna PV (nuvärde), NPV (nettovärde) och FV (framtidsvärde) i Excel 2016 finns alla på finansknappens rullgardinsmeny på menyfliksområdets formlerfliken (Alt+MI) gör att du kan bestämma lönsamheten av en investering.
Funktionen PV, eller Nuvärde, returnerar nuvärdet av en investering, vilket är det totala belopp som en serie framtida betalningar är värda för närvarande. Syntaxen för PV-funktionen är som följer:
=PV(hastighet,nper,pmt,[fv],[typ])
De fv och typ argument är valfria argument i funktionen (anges med hakparenteser). Den fv argumentet är det framtida värdet eller saldot som du vill ha efter att din senaste betalning. Om du utelämnar argumentet fv antar Excel ett framtida värde på noll (0). Den typ argumentet anger om betalning sker i början eller slutet av perioden: Ange 0 (eller utelämna typ argument) när betalningen sker vid slutet av perioden, och använda ett när den är gjord i början av perioden.
Följande bild innehåller flera exempel på användning av PV-funktionen. Alla tre PV-funktionerna använder samma årliga procentsats på 1,25 procent och löptid på 10 år. Eftersom betalningar görs månadsvis omvandlar varje funktion dessa årssiffror till månatliga. Till exempel, i PV-funktionen i cell E3, omvandlas den årliga räntan i cell A3 till en månadsränta genom att dividera med 12 (A3/12). Den årliga termen i cell B3 omvandlas till motsvarande månadsperioder genom att multiplicera med 12 (B3 x 12).
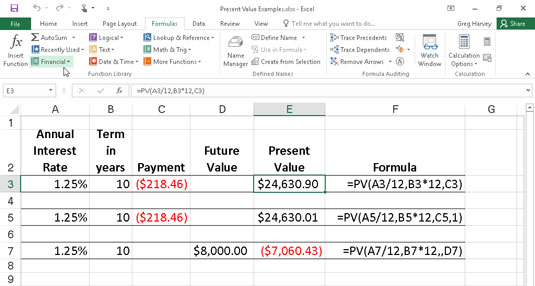
Använda PV-funktionen för att beräkna nuvärdet av olika investeringar.
Observera att även om PV-funktionerna i cellerna E3 och E5 använder argumenten rate, nper och pmt ($218,46), är deras resultat något annorlunda. Detta orsakas av skillnaden i typ argumentet i de två funktionerna: PV-funktionen i cellen E3 antar att varje betalning sker vid slutet av perioden (den typ argumentet är 0 när den är utelämnad), medan PV-funktionen i cell E5 antar att varje betalning sker i början av perioden (anges med en typ argument 1). När betalningen görs i början av perioden, är nuvärdet av denna investering 0,89 USD högre än när betalningen görs i slutet av perioden, vilket återspeglar den ränta som uppstått under den senaste perioden.
Det tredje exemplet i cell E7 (visas i figur 4-1) använder PV-funktionen med ett fv- argument istället för pmt- argumentet. I det här exemplet anger PV-funktionen att du skulle behöva göra månatliga betalningar på 7 060,43 USD under en 10-årsperiod för att realisera ett kassasaldo på 8 000 USD, förutsatt att investeringen gav en konstant årlig ränta på 1 1/4 procent. Observera att när du använder PV-funktionen med fv- argumentet istället för pmt- argumentet, måste du fortfarande ange positionen för pmt- argumentet i funktionen med ett kommatecken (alltså de två kommatecken i rad i funktionen) så att Excel inte Förväxla inte ditt fv- argument med pmt- argumentet.
NPV-funktionen beräknar nettonuvärdet baserat på en serie kassaflöden. Syntaxen för denna funktion är
=NPV( rate , value1 ,[ value2 ],[...])
där värde1, värde2, och så vidare är mellan 1 och 13 värdeargument som representerar en serie betalningar (negativa värden) och inkomster (positiva värden), som var och en är jämnt fördelade i tid och inträffar i slutet av perioden. NPV-investeringen börjar en period före perioden för värde1 kassaflödet och slutar med det sista kassaflödet i argumentlistan. Om ditt första kassaflöde inträffar i början av perioden måste du lägga till det i resultatet av NPV-funktionen istället för att inkludera det som ett av argumenten.
Följande figur illustrerar användningen av NPV-funktionen för att utvärdera attraktiviteten hos en femårig investering som kräver en initial investering på 30 000 USD (värdet i cell G3). Det första året förväntar du dig en förlust på $22 000 (cell B3); det andra året, en vinst på $15 000 (cell C3); det tredje året, en vinst på $25 000 (cell D3); det fjärde året, en vinst på $32 000 (cell E3); och det femte året en vinst på $38 000 (cell F3). Observera att dessa cellreferenser används som värde argument NPV-funktionen.
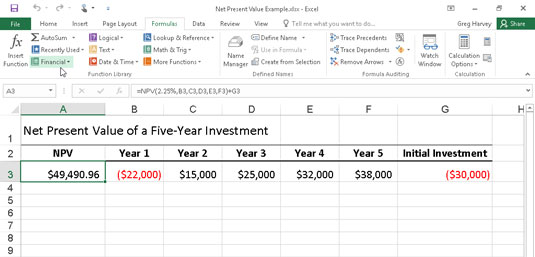
Använda NPV-funktionen för att beräkna nettonuvärdet av en investering.
Till skillnad från när du använder PV-funktionen, kräver NPV-funktionen inte en jämn ström av kassaflöden. Den hastighet argumentet i funktionen är satt till 2,25 procent. I det här exemplet representerar detta investeringens diskonteringsränta – det vill säga den ränta som du kan förvänta dig att få under femårsperioden om du lägger dina pengar på någon annan typ av investering, till exempel en högavkastande pengar -marknadskonto. Denna NPV-funktion i cell A3 returnerar ett nettonuvärde på 49 490,96 USD, vilket indikerar att du kan förvänta dig att realisera mycket mer av att investera dina 30 000 USD i denna investering än vad du möjligen skulle kunna av att investera pengarna på ett penningmarknadskonto till räntan på 2,25 procent.
FV-funktionen beräknar det framtida värdet av en investering. Syntaxen för denna funktion är
=FV(hastighet,nper,pmt,[pv],[typ])
De hastighets, periodantal, PMT, och typ argument är desamma som de som används av den PV-funktionen. Den pv Argumentet är nuvärdet eller schablonbelopp som du vill beräkna det framtida värdet. Precis som med argumenten fv och typ i PV-funktionen, är både argumenten pv och typ valfria i FV-funktionen. Om du utelämnar dessa argument antar Excel att deras värden är noll (0) i funktionen.
Du kan använda FV-funktionen för att beräkna det framtida värdet av en investering, till exempel ett IRA (Individual Retirement Account). Anta till exempel att du etablerar en IRA vid 43 års ålder och går i pension om 22 år vid 65 års ålder och att du planerar att göra årliga inbetalningar till IRA i början av varje år. Om du antar en avkastning på 2,5 procent per år, skulle du ange följande FV-funktion i ditt kalkylblad:
=FV(2,5 %;22;–1500;,1)
Excel anger sedan att du kan förvänta dig ett framtida värde på 44 376,64 USD för din IRA när du går i pension vid 65 års ålder. Om du hade etablerat IRA ett år tidigare och kontot redan har ett nuvärde på 1 538 USD, skulle du ändra FV-funktionen enligt följande :
=FV(2,5 %;22;–1500;–1538;1)
I det här fallet indikerar Excel att du kan förvänta dig ett framtida värde på $47 024,42 för din IRA vid pensioneringen.
Hur man blockerar Microsoft Word från att öppna filer i skrivskyddat läge på Windows Microsoft Word öppnar filer i skrivskyddat läge, vilket gör det omöjligt att redigera dem? Oroa dig inte, metoderna finns nedan
Så här åtgärdar du fel vid utskrift av felaktiga Microsoft Word-dokument Fel vid utskrift av Word-dokument med ändrade teckensnitt, röriga stycken, saknad text eller förlorat innehåll är ganska vanligt. Men gör det inte
Om du har använt pennan eller överstrykningspennan för att rita på dina PowerPoint-bilder under en presentation, kan du spara ritningarna till nästa presentation eller radera dem så att nästa gång du visar den börjar du med rena PowerPoint-bilder. Följ dessa instruktioner för att radera ritningar med penna och överstrykningspenna: Radera linjer ett på […]
Stilbiblioteket innehåller CSS-filer, XSL-filer (Extensible Stylesheet Language) och bilder som används av fördefinierade mallsidor, sidlayouter och kontroller i SharePoint 2010. För att hitta CSS-filer i stilbiblioteket på en publiceringswebbplats: Välj Webbplatsåtgärder→Visa Allt webbplatsinnehåll. Innehållet på webbplatsen visas. Style-biblioteket ligger i […]
Överväldiga inte din publik med gigantiska siffror. I Microsoft Excel kan du förbättra läsbarheten för dina instrumentpaneler och rapporter genom att formatera dina siffror så att de visas i tusentals eller miljoner.
Lär dig hur du använder SharePoints sociala nätverksverktyg som låter individer och grupper kommunicera, samarbeta, dela och ansluta.
Julianska datum används ofta i tillverkningsmiljöer som en tidsstämpel och snabbreferens för ett batchnummer. Denna typ av datumkodning tillåter återförsäljare, konsumenter och serviceagenter att identifiera när en produkt tillverkades och därmed produktens ålder. Julianska datum används också i programmering, militären och astronomi. Annorlunda […]
Du kan skapa en webbapp i Access 2016. Så vad är en webbapp egentligen? Tja, webben betyder att den är online, och appen är bara en förkortning för "applikation". En anpassad webbapp är en onlinedatabasapplikation som nås från molnet med en webbläsare. Du bygger och underhåller webbappen i skrivbordsversionen […]
De flesta sidor i SharePoint 2010 visar en lista med navigeringslänkar i snabbstartsfältet till vänster på sidan. Snabbstartsfältet visar länkar till utvalt webbplatsinnehåll som listor, bibliotek, webbplatser och publiceringssidor. Snabbstartsfältet innehåller två mycket viktiga länkar: Länken Allt webbplatsinnehåll: […]
För enkla problem hittar Solver i Excel vanligtvis snabbt de optimala Solver-variabelvärdena för objektivfunktionen. Men i vissa fall har Solver problem med att hitta Solver-variabelvärdena som optimerar objektivfunktionen. I dessa fall visar Solver vanligtvis ett meddelande eller ett felmeddelande som beskriver eller diskuterar problemet som […]
