Rörliga medelvärden i Excel Data Analysis Add-in

När du har installerat Excel Data Analysis-tillägget och gjort det tillgängligt för Excel kan du välja vilket som helst av dess analysverktyg och köra den analysen på indata som du tillhandahåller. I prognosvärlden betyder det baslinjen som du har samlat in och strukturerat ordentligt på ett kalkylblad.

Det första verktyget du kan överväga - om än bara för att det är det enklaste att använda och förstå - är verktyget Moving Average. Som alltid med tillägget, börja med att gå till menyfliksområdet Data och välja Dataanalys. I listrutan Analysverktyg väljer du glidande medelvärde och klickar på OK.

Dialogrutan för glidande medelvärde, som visas här, visas.

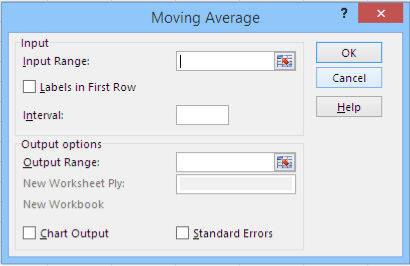
Intervallet är antalet faktiska värden från din baslinje som ska användas i varje glidande medelvärde.

Flyttdag: Att ta sig härifrån till dit

Lika lätt som glidande medelvärden är att ställa in och förstå, du tar ett extra ansvar när du bestämmer dig för att prognostisera med dem. Frågan är hur många tidsperioder från din baslinje du bör inkludera i varje glidande medelvärde.

Använd samma antal faktiska observationer för att beräkna varje glidande medelvärde. Om det första glidande medelvärdet som du har Excel beräknat använder tre perioder från baslinjen, använder alla glidande medelvärden i din prognos tre perioder.

Du vill välja rätt antal perioder:

• Om du använder för få kommer prognoserna att svara på slumpmässiga chocker i baslinjen, när det du är ute efter är att jämna ut de slumpmässiga felen och fokusera på de verkliga drivkrafterna för dina försäljningsresultat.
• Om du använder för många, släpar prognoserna efter verkliga, ihållande förändringar i nivån på baslinjen - kanske för långt för att du ska kunna reagera effektivt.

När du bestämmer dig för att använda verktyget glidande medelvärde – eller mer allmänt, att använda glidande medelvärden oavsett om du använder verktyget eller anger formlerna själv – tar du ställning till effekten av de senaste baslinjevärdena kontra effekten av fler avlägsna baslinjevärden.

Anta att du har en baslinje som sträcker sig från januari 2016 till december 2016, och du använder ett tre månaders glidande medelvärde av försäljningsresultat för dina prognoser. Prognosen för januari 2017 skulle vara genomsnittet av resultaten från oktober, november och december 2016. Den prognosen är helt beroende av det sista kvartalet 2016 och är matematiskt oberoende av de tre första kvartalen 2016.

Tänk om du istället hade valt ett sexmånaders glidande medelvärde? Då skulle prognosen för januari 2017 baseras på genomsnittet för juli till och med december 2016. Den skulle vara helt beroende av andra halvan av 2016, och första halvan av 2016 skulle inte ha någon direkt inverkan på januari 2017-prognosen.

Det kan mycket väl vara så att någon av dessa situationer - eller en annan, till exempel ett tvåmånaders glidande medelvärde - är precis vad du vill ha. Till exempel kan du behöva din prognos för att betona de senaste resultaten. Den betoningen kan vara särskilt viktig om du misstänker att en nyligen genomförd händelse, till exempel en betydande förändring av din produktlinje, kommer att påverka försäljningen.

Å andra sidan kanske du inte vill betona de senaste försäljningsresultaten för mycket. Att betona de senaste försäljningsresultaten kan dölja vad som händer med din baslinje på lång sikt. Om du inte är säker på hur mycket du ska betona de senaste resultaten har du ett par bra alternativ:

• Experimentera med olika antal tidsperioder för att göra upp dina glidande medelvärden. Detta tillvägagångssätt är ofta bäst.
• Använd exponentiell utjämning, som använder hela baslinjen för att få en prognos men ger större vikt åt de nyare baslinjevärdena. Exponentiell utjämning ger lite mindre vikt åt det näst sista baslinjevärdet, lite mindre vikt till det före det, och så vidare hela vägen tillbaka till det första baslinjevärdet, som har minst inflytande på nästa prognos.

Rörliga medelvärden och stationära baslinjer

Rörliga medelvärden är väl lämpade för stationära baslinjer (baslinjer vars nivåer i allmänhet inte ökar eller minskar under en lång tidsperiod). Du kan använda glidande medelvärden med baslinjer som trendar uppåt eller nedåt, men du bör vanligtvis avskräcka dem först eller använda en av de mer komplicerade modellerna för glidande medelvärde.

Hur skiljer man en stationär baslinje från en som trendar uppåt eller nedåt? Ett sätt är att se på det. Följande figur har ett exempel. Baslinjen ser verkligen stationär ut. Den har toppar och toppar och dalar, men totalt sett verkar baslinjen inte trenda upp eller ner.

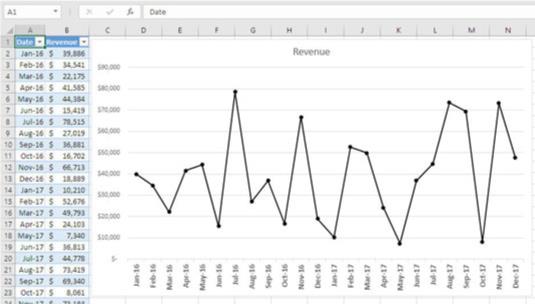
Över en längre tidsperiod (säg sex år snarare än två) kan denna baslinje visa sig vara en del av en cykel. Men för kortsiktiga syften är detta en stationär baslinje.

Problemet med att bara titta på baslinjen är att det ibland inte är helt klart om det är stationärt eller trendigt. Vad tycker du om baslinjen som visas i följande figur? Om man tittar på diagrammet är det svårt att säga om baslinjen är stationär. Det kan det vara, men det kan verkligen sjunka gradvis. Du kan göra ett snabbtest genom att kontrollera korrelationen mellan datum och intäkt.

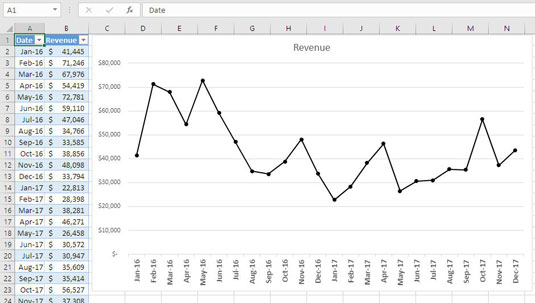
Den här baslinjen ser ut som om den kan vara på väg neråt. Att lägga till en trendlinje kan hjälpa dig att tolka vad som händer.