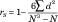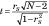Spearmans korrelationskoefficient, rS, var det tidigaste icke-parametriska testet baserat på rangordningar. För ett urval av individer som var och en mätt på två variabler i Excel är tanken att rangordna varje poäng inom sin egen variabel. Subtrahera sedan en rang från den andra för varje individ. Om korrelationen är perfekt (i positiv riktning) är alla skillnader noll.
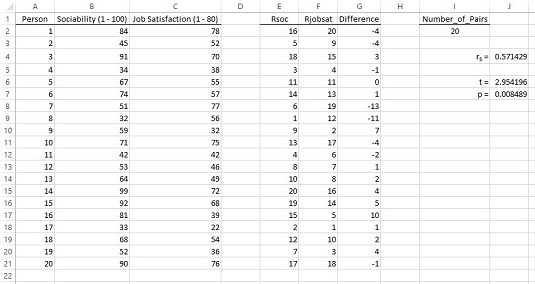
Bilden nedan visar ett exempel. En industripsykolog bedömde sällskapligheten hos 20 anställda på FarDrate Timepiece Corporation. Skalan sträckte sig från 1 (minst sällskaplig) till 100 (mest sällskaplig). Varje FarDrate-anställd bedömde också sin arbetstillfredsställelse på en skala från 1 (minst nöjd) till 80 (mest nöjd). Nollhypotesen är att sällskaplighet inte är korrelerad med arbetstillfredsställelse. Den alternativa hypotesen är att dessa två variabler är korrelerade.
Uppgifterna finns i kolumnerna B och C, och rangorden finns i kolumnerna E och F. Skillnaderna mellan varje rangpar finns i kolumn G.
Spearman's rS.
Formeln är
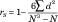
där d är en interparskillnad. Som är fallet med den vanliga korrelationskoefficienten, om nollhypotesen är sann, bör värdet på rS vara runt noll.
För att beräkna rangen i kolumn E, skriv
=RANK.AVG(B2,$B$2:$B$21,1)
i E2 och autofylld. För rangorden i kolumn E, skriv
=RANK.AVG(C2,$C$2:$C$21,1)
till F2 och autofylld.
Du behöver inte skriva in en komplicerad Excel-formel i cell J4 för att beräkna korrelationskoefficienten. Varför? Eftersom Excel och matematisk statistik slår sig samman för en kraftig överraskning: Allt du behöver göra är att skriva
=CORREL(E2:E21;F2:F21)
in i J4. Det är allt som finns. Att använda CORREL på rangorden ger samma svar som formeln ovan. (Så det är egentligen inte nödvändigt att beräkna rangskillnaderna mellan par i kolumn G.)
Beräkna
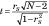
N är antalet par, och testet har N-2 frihetsgrader.
Du kan definiera Antal_par som namn på värdet i cell I2. Så typ
=J4*SQRT(Antal_par-2)/SQRT(1-J4^2)
in i J6 och
=T.FÖRD.2T(J6,Antal_par-2)
in i J7. Du kan använda den tvåsidiga t-fördelningsfunktionen om du inte känner till korrelationens riktning i förväg. Och återigen säger det låga p-värdet dig att förkasta nollhypotesen.
Lär dig att använda kommandona Gör om och Upprepa i Word 2016 för att effektivt hantera dina dokument. Dessa funktioner hjälper dig att enkelt ångra och återställa ändringar.
Hur man blockerar Microsoft Word från att öppna filer i skrivskyddat läge på Windows Microsoft Word öppnar filer i skrivskyddat läge, vilket gör det omöjligt att redigera dem? Oroa dig inte, metoderna finns nedan
Så här åtgärdar du fel vid utskrift av felaktiga Microsoft Word-dokument Fel vid utskrift av Word-dokument med ändrade teckensnitt, röriga stycken, saknad text eller förlorat innehåll är ganska vanligt. Men gör det inte
Om du har använt pennan eller överstrykningspennan för att rita på dina PowerPoint-bilder under en presentation, kan du spara ritningarna till nästa presentation eller radera dem så att nästa gång du visar den börjar du med rena PowerPoint-bilder. Följ dessa instruktioner för att radera ritningar med penna och överstrykningspenna: Radera linjer ett på […]
Stilbiblioteket innehåller CSS-filer, XSL-filer (Extensible Stylesheet Language) och bilder som används av fördefinierade mallsidor, sidlayouter och kontroller i SharePoint 2010. För att hitta CSS-filer i stilbiblioteket på en publiceringswebbplats: Välj Webbplatsåtgärder→Visa Allt webbplatsinnehåll. Innehållet på webbplatsen visas. Style-biblioteket ligger i […]
Överväldiga inte din publik med gigantiska siffror. I Microsoft Excel kan du förbättra läsbarheten för dina instrumentpaneler och rapporter genom att formatera dina siffror så att de visas i tusentals eller miljoner.
Lär dig hur du använder SharePoints sociala nätverksverktyg som låter individer och grupper kommunicera, samarbeta, dela och ansluta.
Julianska datum används ofta i tillverkningsmiljöer som en tidsstämpel och snabbreferens för ett batchnummer. Denna typ av datumkodning tillåter återförsäljare, konsumenter och serviceagenter att identifiera när en produkt tillverkades och därmed produktens ålder. Julianska datum används också i programmering, militären och astronomi. Annorlunda […]
Du kan skapa en webbapp i Access 2016. Så vad är en webbapp egentligen? Tja, webben betyder att den är online, och appen är bara en förkortning för "applikation". En anpassad webbapp är en onlinedatabasapplikation som nås från molnet med en webbläsare. Du bygger och underhåller webbappen i skrivbordsversionen […]
De flesta sidor i SharePoint 2010 visar en lista med navigeringslänkar i snabbstartsfältet till vänster på sidan. Snabbstartsfältet visar länkar till utvalt webbplatsinnehåll som listor, bibliotek, webbplatser och publiceringssidor. Snabbstartsfältet innehåller två mycket viktiga länkar: Länken Allt webbplatsinnehåll: […]
