Funktionen nettonuvärde (NPV) i Excel 2013 beräknar nettonuvärdet baserat på en serie kassaflöden. Syntaxen för denna funktion är
=NPV( rate , value1 ,[ value2 ],[...])
där värde1, värde2, och så vidare är mellan 1 och 13 värdeargument som representerar en serie betalningar (negativa värden) och inkomster (positiva värden), som var och en är jämnt fördelade i tid och inträffar i slutet av perioden.
NPV-investeringen börjar en period före perioden för värde1 kassaflödet och slutar med det sista kassaflödet i argumentlistan. Om ditt första kassaflöde inträffar i början av perioden måste du lägga till det i resultatet av NPV-funktionen istället för att inkludera det som ett av argumenten.
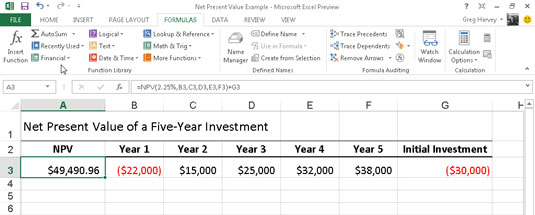
Figuren illustrerar användningen av NPV-funktionen för att utvärdera attraktiviteten hos en femårig investering som kräver en initial investering på 30 000 USD (värdet i cell G3).
Det första året förväntar du dig en förlust på $22 000 (cell B3); det andra året, en vinst på $15 000 (cell C3); det tredje året, en vinst på $25 000 (cell D3); det fjärde året, en vinst på $32 000 (cell E3); och det femte året en vinst på $38 000 (cell F3). Observera att dessa cellreferenser används som värde argument NPV-funktionen.
Till skillnad från när du använder PV-funktionen, kräver NPV-funktionen inte en jämn ström av kassaflöden. Den hastighet argumentet i funktionen är satt till 2,25 procent. I det här exemplet representerar detta investeringens diskonteringsränta – det vill säga den ränta som du kan förvänta dig att få under femårsperioden om du lägger dina pengar på någon annan typ av investering, till exempel en högavkastande pengar -marknadskonto.
Denna NPV-funktion i cell A3 returnerar ett nettonuvärde på 49 490,96 USD, vilket indikerar att du kan förvänta dig att realisera mycket mer av att investera dina 30 000 USD i denna investering än vad du möjligen skulle kunna av att investera pengarna på ett penningmarknadskonto till räntan på 2,25 procent.
Lär dig att använda kommandona Gör om och Upprepa i Word 2016 för att effektivt hantera dina dokument. Dessa funktioner hjälper dig att enkelt ångra och återställa ändringar.
Hur man blockerar Microsoft Word från att öppna filer i skrivskyddat läge på Windows Microsoft Word öppnar filer i skrivskyddat läge, vilket gör det omöjligt att redigera dem? Oroa dig inte, metoderna finns nedan
Så här åtgärdar du fel vid utskrift av felaktiga Microsoft Word-dokument Fel vid utskrift av Word-dokument med ändrade teckensnitt, röriga stycken, saknad text eller förlorat innehåll är ganska vanligt. Men gör det inte
Om du har använt pennan eller överstrykningspennan för att rita på dina PowerPoint-bilder under en presentation, kan du spara ritningarna till nästa presentation eller radera dem så att nästa gång du visar den börjar du med rena PowerPoint-bilder. Följ dessa instruktioner för att radera ritningar med penna och överstrykningspenna: Radera linjer ett på […]
Stilbiblioteket innehåller CSS-filer, XSL-filer (Extensible Stylesheet Language) och bilder som används av fördefinierade mallsidor, sidlayouter och kontroller i SharePoint 2010. För att hitta CSS-filer i stilbiblioteket på en publiceringswebbplats: Välj Webbplatsåtgärder→Visa Allt webbplatsinnehåll. Innehållet på webbplatsen visas. Style-biblioteket ligger i […]
Överväldiga inte din publik med gigantiska siffror. I Microsoft Excel kan du förbättra läsbarheten för dina instrumentpaneler och rapporter genom att formatera dina siffror så att de visas i tusentals eller miljoner.
Lär dig hur du använder SharePoints sociala nätverksverktyg som låter individer och grupper kommunicera, samarbeta, dela och ansluta.
Julianska datum används ofta i tillverkningsmiljöer som en tidsstämpel och snabbreferens för ett batchnummer. Denna typ av datumkodning tillåter återförsäljare, konsumenter och serviceagenter att identifiera när en produkt tillverkades och därmed produktens ålder. Julianska datum används också i programmering, militären och astronomi. Annorlunda […]
Du kan skapa en webbapp i Access 2016. Så vad är en webbapp egentligen? Tja, webben betyder att den är online, och appen är bara en förkortning för "applikation". En anpassad webbapp är en onlinedatabasapplikation som nås från molnet med en webbläsare. Du bygger och underhåller webbappen i skrivbordsversionen […]
De flesta sidor i SharePoint 2010 visar en lista med navigeringslänkar i snabbstartsfältet till vänster på sidan. Snabbstartsfältet visar länkar till utvalt webbplatsinnehåll som listor, bibliotek, webbplatser och publiceringssidor. Snabbstartsfältet innehåller två mycket viktiga länkar: Länken Allt webbplatsinnehåll: […]
