Poisson kan vara ett mycket användbart verktyg när man närmar sig statistisk analys med Excel. Inte visa hur det fungerar? Här är stegen för att använda Excels POISSON.DIST:
Välj en cell för POISSON.DIST:s svar.
Från menyn Statistiska funktioner, välj POISSON.DIST för att öppna dialogrutan Funktionsargument.
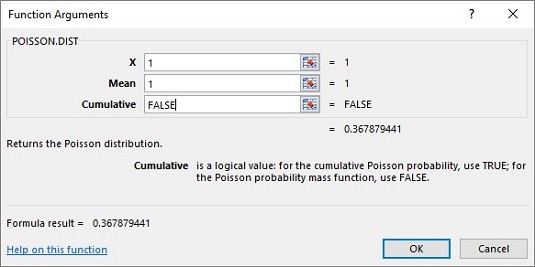
I dialogrutan Funktionsargument anger du lämpliga värden för argumenten.
I X-rutan anger du antalet händelser som du bestämmer sannolikheten för. För det här exemplet letar du efter pr (1), så skriv in 1.
I rutan Medel anger du processens medelvärde, vilket för det här exemplet är 1.
I rutan Kumulativ är det antingen TRUE för den kumulativa sannolikheten eller FALSK för bara sannolikheten för antalet händelser. Ange FALSE.
Med posterna för X, Mean och Cumulative visas svaret i dialogrutan. Svaret för detta exempel är .367879441.
Klicka på OK för att lägga svaret i den valda cellen.
I exemplet ser du sannolikheten för två defekta leder i 1 000 och sannolikheten för tre. För att fortsätta med beräkningarna, skriv 2 i X-rutan för att beräkna pr (2) och 3 för att hitta pr (3).
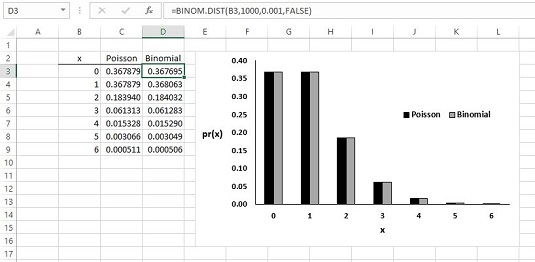
På 2000-talet är det ganska lätt att beräkna de binomiska sannolikheterna direkt. Bilden nedan visar Poisson- och binomialsannolikheterna för talen i kolumn B och villkoren för exemplet. Sannolikheterna är grafiska så att du kan se hur nära de två verkligen är. Cell D3 valdes, så formelfältet visar hur BINOM.DIST användes för att beräkna binomialsannolikheterna.
Även om Poissons användbarhet som uppskattning är föråldrad, har den fått sitt eget liv. Fenomen som är så vitt skilda som reaktionstidsdata i psykologiska experiment, degenerering av radioaktiva ämnen och poäng i professionella hockeyspel verkar passa Poisson-fördelningarna. Det är därför affärsanalytiker och vetenskapliga forskare gillar att basera modeller på denna fördelning.
Hur man blockerar Microsoft Word från att öppna filer i skrivskyddat läge på Windows Microsoft Word öppnar filer i skrivskyddat läge, vilket gör det omöjligt att redigera dem? Oroa dig inte, metoderna finns nedan
Så här åtgärdar du fel vid utskrift av felaktiga Microsoft Word-dokument Fel vid utskrift av Word-dokument med ändrade teckensnitt, röriga stycken, saknad text eller förlorat innehåll är ganska vanligt. Men gör det inte
Om du har använt pennan eller överstrykningspennan för att rita på dina PowerPoint-bilder under en presentation, kan du spara ritningarna till nästa presentation eller radera dem så att nästa gång du visar den börjar du med rena PowerPoint-bilder. Följ dessa instruktioner för att radera ritningar med penna och överstrykningspenna: Radera linjer ett på […]
Stilbiblioteket innehåller CSS-filer, XSL-filer (Extensible Stylesheet Language) och bilder som används av fördefinierade mallsidor, sidlayouter och kontroller i SharePoint 2010. För att hitta CSS-filer i stilbiblioteket på en publiceringswebbplats: Välj Webbplatsåtgärder→Visa Allt webbplatsinnehåll. Innehållet på webbplatsen visas. Style-biblioteket ligger i […]
Överväldiga inte din publik med gigantiska siffror. I Microsoft Excel kan du förbättra läsbarheten för dina instrumentpaneler och rapporter genom att formatera dina siffror så att de visas i tusentals eller miljoner.
Lär dig hur du använder SharePoints sociala nätverksverktyg som låter individer och grupper kommunicera, samarbeta, dela och ansluta.
Julianska datum används ofta i tillverkningsmiljöer som en tidsstämpel och snabbreferens för ett batchnummer. Denna typ av datumkodning tillåter återförsäljare, konsumenter och serviceagenter att identifiera när en produkt tillverkades och därmed produktens ålder. Julianska datum används också i programmering, militären och astronomi. Annorlunda […]
Du kan skapa en webbapp i Access 2016. Så vad är en webbapp egentligen? Tja, webben betyder att den är online, och appen är bara en förkortning för "applikation". En anpassad webbapp är en onlinedatabasapplikation som nås från molnet med en webbläsare. Du bygger och underhåller webbappen i skrivbordsversionen […]
De flesta sidor i SharePoint 2010 visar en lista med navigeringslänkar i snabbstartsfältet till vänster på sidan. Snabbstartsfältet visar länkar till utvalt webbplatsinnehåll som listor, bibliotek, webbplatser och publiceringssidor. Snabbstartsfältet innehåller två mycket viktiga länkar: Länken Allt webbplatsinnehåll: […]
För enkla problem hittar Solver i Excel vanligtvis snabbt de optimala Solver-variabelvärdena för objektivfunktionen. Men i vissa fall har Solver problem med att hitta Solver-variabelvärdena som optimerar objektivfunktionen. I dessa fall visar Solver vanligtvis ett meddelande eller ett felmeddelande som beskriver eller diskuterar problemet som […]
