Fliken GRG olinjär i Excel innehåller knappar och rutor för att hantera hur Solver fungerar när du använder GRG olinjär lösningsmetoden. Detta kan vara något du aldrig kommer att behöva, men det är bra att ha möjligheten.
Har du någonsin varit på en restaurang där din server går omkring någon gång under måltiden med en enorm pepparkvarn och frågar om du vill ha svartpeppar på din sallad? Om du har, vet du att en del av ritualen är att du någon gång berättar för servern när hon har mald tillräckligt med peppar för din grönsallad.
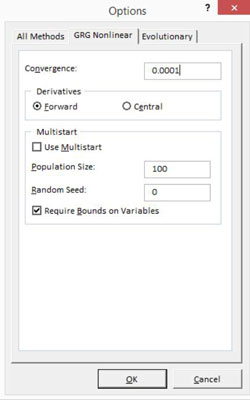
Textrutan Konvergens som finns på fliken GRG icke-linjär i dialogrutan Lösningsalternativ fungerar på ungefär samma sätt. Om du använder metoden GRG Nolinear Solving använder du konvergensrutan för att tala om för Excel när det ska sluta leta efter en bättre lösning. Textrutan Konvergens accepterar alla värden mellan 0 och 1.
När förändringen i resultatet av målfunktionsformeln är mindre än värdet som visas i konvergenstextrutan, räknar Excel med att saker och ting närmar sig tillräckligt, så ytterligare iterationer är inte nödvändiga.
Åh, och något du borde veta: Med större konvergensvärden når Excel en rimlig lösning snabbare och med mindre arbete. Och med mindre eller mycket exakta konvergensvärden arbetar Excel hårdare och tar längre tid.
Välj bland de två alternativknapparna för derivator — Framåt och Central — för att berätta för Excel hur man uppskattar partiella derivator när det arbetar med målfunktionen och begränsningsformlerna. I de flesta fall fungerar allt bra om Excel använder framåtderivata. Men i vissa fall fungerar inte terminsderivat. Och i den här situationen kanske du kan ange att Excel använder centrala derivator.
Att använda centrala derivator kräver mycket mer arbete med Excel, men vissa mycket begränsade problem kan lättare och mer praktiskt lösas med hjälp av centrala derivator.
Om du markerar rutan Multistart på fliken GRG Nolinjär, säger du till Solver att i praktiken lösa optimeringsproblemet genom att börja från flera olika utgångspunkter. Rutan Populationsstorlek låter dig ange antalet startpunkter. Rutan Random Seed låter dig ange ett heltal som ska användas som frö till en slumptalsgenerator som producerar de faktiska startpunkterna.
Slutligen kan du markera och avmarkera rutan Require Bounds On Variables för att specificera att hela multistartsvansinnet bara inträffar när du har haft anständigheten att definiera både övre och nedre gränser för variablerna.
Lär dig att använda kommandona Gör om och Upprepa i Word 2016 för att effektivt hantera dina dokument. Dessa funktioner hjälper dig att enkelt ångra och återställa ändringar.
Hur man blockerar Microsoft Word från att öppna filer i skrivskyddat läge på Windows Microsoft Word öppnar filer i skrivskyddat läge, vilket gör det omöjligt att redigera dem? Oroa dig inte, metoderna finns nedan
Så här åtgärdar du fel vid utskrift av felaktiga Microsoft Word-dokument Fel vid utskrift av Word-dokument med ändrade teckensnitt, röriga stycken, saknad text eller förlorat innehåll är ganska vanligt. Men gör det inte
Om du har använt pennan eller överstrykningspennan för att rita på dina PowerPoint-bilder under en presentation, kan du spara ritningarna till nästa presentation eller radera dem så att nästa gång du visar den börjar du med rena PowerPoint-bilder. Följ dessa instruktioner för att radera ritningar med penna och överstrykningspenna: Radera linjer ett på […]
Stilbiblioteket innehåller CSS-filer, XSL-filer (Extensible Stylesheet Language) och bilder som används av fördefinierade mallsidor, sidlayouter och kontroller i SharePoint 2010. För att hitta CSS-filer i stilbiblioteket på en publiceringswebbplats: Välj Webbplatsåtgärder→Visa Allt webbplatsinnehåll. Innehållet på webbplatsen visas. Style-biblioteket ligger i […]
Överväldiga inte din publik med gigantiska siffror. I Microsoft Excel kan du förbättra läsbarheten för dina instrumentpaneler och rapporter genom att formatera dina siffror så att de visas i tusentals eller miljoner.
Lär dig hur du använder SharePoints sociala nätverksverktyg som låter individer och grupper kommunicera, samarbeta, dela och ansluta.
Julianska datum används ofta i tillverkningsmiljöer som en tidsstämpel och snabbreferens för ett batchnummer. Denna typ av datumkodning tillåter återförsäljare, konsumenter och serviceagenter att identifiera när en produkt tillverkades och därmed produktens ålder. Julianska datum används också i programmering, militären och astronomi. Annorlunda […]
Du kan skapa en webbapp i Access 2016. Så vad är en webbapp egentligen? Tja, webben betyder att den är online, och appen är bara en förkortning för "applikation". En anpassad webbapp är en onlinedatabasapplikation som nås från molnet med en webbläsare. Du bygger och underhåller webbappen i skrivbordsversionen […]
De flesta sidor i SharePoint 2010 visar en lista med navigeringslänkar i snabbstartsfältet till vänster på sidan. Snabbstartsfältet visar länkar till utvalt webbplatsinnehåll som listor, bibliotek, webbplatser och publiceringssidor. Snabbstartsfältet innehåller två mycket viktiga länkar: Länken Allt webbplatsinnehåll: […]
