Hur du ställer in din Excel-försäljningsprognos

Det enklaste sättet att få en försäljningsprognos är att lägga ut din baslinje på ett Excel-kalkylblad i en tabellkonfiguration och sedan använda tillägget Data Analysis för att generera en prognos åt dig. Det tillägget följer med Microsoft Office.

Tillägget och dess verktyg är goda och dåliga nyheter - mer bra än dåliga, faktiskt. Det har inte förändrats nämnvärt sedan Excel 1995, förutom att nu koden är skriven med Visual Basic snarare än det gamla konstiga Excel 4.0-makrospråket. Det kan vara udda, som du kommer att se om du bestämmer dig för att använda det. Trots dess egenheter kan det spara lite tid. Det kan fungera som en ganska bra språngbräda för att lära sig hur man gör allt själv. Och det kan bespara dig de fel som oundvikligen uppstår när du rullar dina egna prognoser.

Tillägget har 19 olika numeriska och statistiska analysverktyg. Om du lägger upp din data på rätt sätt kan du rikta ett av dess verktyg mot din data och få en ganska komplett och vanligtvis korrekt analys — inklusive autokorrelationsanalyser, prognoser för glidande medelvärde, exponentiellt utjämnande prognoser och regressionsprognoser. Det gör det hårda arbetet för dig, och eftersom det hela är förkodat behöver du inte oroa dig så mycket för att till exempel få en fel formel.

Utjämna data

Om du bestämmer dig för att använda exponentiell utjämning för att skapa din prognos, behöver du bara baslinjen för historiska försäljningsintäkter. Varje observation i baslinjen bör vara från samma sorts prognosperiod – så ofta som inte, totala intäkter på månadsbasis.

Du behöver ingen annan variabel än dina försäljningsresultat eftersom, med utjämning, kommer du att använda en periods resultat för att prognostisera nästa – vilket är en anledning till att du använder dataanalystilläggets korrelationsverktyg för att bestämma mängden autokorrelation i baslinjen innan du gör prognosen. Betydande autokorrelation tenderar att leda dig mot att använda verktyget exponentiell utjämning som din prognosmetod - och det kommer att hjälpa dig att bestämma vilken dämpningsfaktor (eller, motsvarande, vilken utjämningskonstant) du ska använda för att utveckla din prognos.

Regression: Allt handlar om relationer

Om du har tillgänglig någon variabel utöver försäljningsintäkter eller sålda enheter, och du misstänker att det är starkt relaterat till försäljningsresultaten, bör du titta närmare på förhållandet.

Anta att du kan lägga vantarna på historiska data som visar - per år och månad, till exempel - enhetspriset som du har debiterat och antalet enheter du har sålt. Om du är intresserad av att prognostisera antalet enheter du kommer att sälja nästa månad, kan Data Analysis-tilläggets regressionsverktyg underlätta din uppgift.

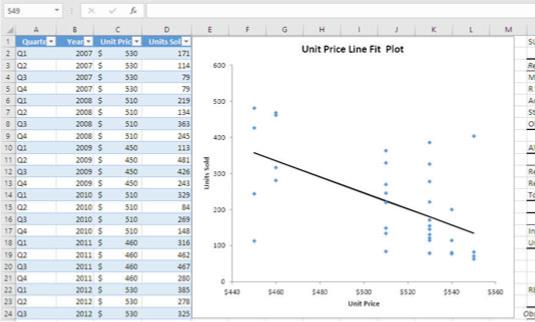
Diagrammet ger dig en bild av vad som händer mellan de två variablerna: Enhetspris och Sålda enheter.

(I figuren har diagrammets utseende ändrats eftersom regressionsverktyget skapar det för att göra det lättare att mäta förhållandet mellan pris och volym.)

Med denna baslinje, inklusive enhetspris och sålda enheter, fokuserar ditt intresse inte på intäkter. När allt kommer omkring är det ganska tydligt från diagrammet att ju högre enhetspris, desto färre enheter såldes - och det tenderar att minimera variationen i kvartalsintäkter. Istället talar denna analys till produktionen. Om du vet hur du kommer att ställa in ditt enhetspris för nästa kvartal, kan du använda regressionsverktyget för att prognostisera antalet enheter du kommer att sälja nästa kvartal. Den prognosen kan mycket väl informera din produktionsavdelning om hur man fördelar sina resurser.

Förresten, Excel benämner den heldragna linjen som visas en trendlinje. När du ser en trendlinje som löper från det övre vänstra till det nedre högra, som visas, vet du att korrelationen mellan de två variablerna är negativ (och i det här fallet är korrelationen mellan enhetspris och sålda enheter –0,57). En negativ korrelation innebär att ju högre nivå en av variablerna har, desto lägre blir motsvarande värde för den andra variabeln. Om trendlinjen går från det nedre vänstra till det övre högra vet du att korrelationen är positiv. En positiv korrelation innebär att lägre värden på en variabel är associerade med lägre värden på den andra och att högre värden på den ena är associerade med högre värden på den andra.