Här är några sannolikhetsrelaterade kalkylbladsfunktioner som du kan använda i Excel 2016 för att hjälpa till med statistisk analys. Även om de är lite på den esoteriska sidan, kanske du kan hitta någon användning för dem.
Om du har en sannolikhetsfördelning av en diskret slumpvariabel och du vill hitta sannolikheten att variabeln får ett visst värde, är PROB något för dig. Här är dialogrutan PROB Argument Functions tillsammans med en distribution.
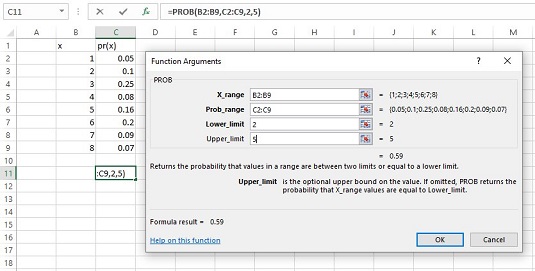
Dialogrutan PROB-funktionsargument och en sannolikhetsfördelning.
Du anger den slumpmässiga variabeln (X_range), sannolikheterna (Prob_range), en nedre gräns och en övre gräns. PROB returnerar sannolikheten att den slumpmässiga variabeln får ett värde mellan dessa gränser (inklusive).
Om du lämnar Övre gräns tom, returnerar PROB sannolikheten för värdet du gav för den nedre gränsen. Om du lämnar den nedre gränsen tom, returnerar PROB sannolikheten att som mest erhålla den övre gränsen (till exempel den kumulativa sannolikheten).
Detta är en sannolikhetstäthetsfunktion som mestadels är tillämplig på teknik. Det fungerar som en modell för tiden tills ett fysiskt system misslyckas. Som ingenjörer vet förblir antalet fel i vissa system detsamma över tid eftersom stötar i systemet orsakar fel. I andra, som vissa mikroelektroniska komponenter, minskar antalet fel med tiden. Hos ytterligare andra ökar slitaget misslyckanden med tiden.
Weibull-fördelningens två parametrar låter den återspegla alla dessa möjligheter. En parameter, Alpha, avgör hur bred eller smal fördelningen är. Den andra, Beta, bestämmer var den är centrerad på x- axeln.
Weibulls sannolikhetstäthetsfunktion är en ganska komplicerad ekvation. Tack vare Excel behöver du inte oroa dig för det. Bilden nedan visar WEIBULL.DIST:s funktionsargument-dialogruta.
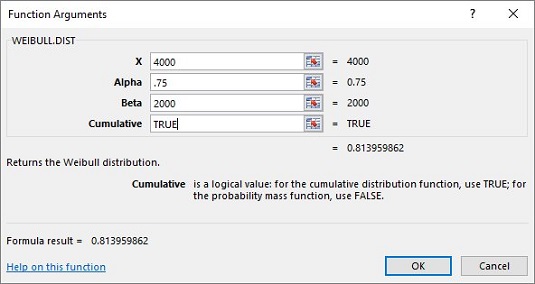
Dialogrutan WEIBULL.DIST Funktionsargument.
Dialogrutan svarar på den typ av fråga som en produkttekniker skulle ställa: Antag att tiden till fel på en glödlampa i en LCD-projektor följer en Weibull-fördelning med Alpha = 0,75 och Beta = 2 000 timmar. Hur stor är sannolikheten att glödlampan håller högst 4 000 timmar? Dialogrutan visar att svaret är .814.
Lär dig att använda kommandona Gör om och Upprepa i Word 2016 för att effektivt hantera dina dokument. Dessa funktioner hjälper dig att enkelt ångra och återställa ändringar.
Hur man blockerar Microsoft Word från att öppna filer i skrivskyddat läge på Windows Microsoft Word öppnar filer i skrivskyddat läge, vilket gör det omöjligt att redigera dem? Oroa dig inte, metoderna finns nedan
Så här åtgärdar du fel vid utskrift av felaktiga Microsoft Word-dokument Fel vid utskrift av Word-dokument med ändrade teckensnitt, röriga stycken, saknad text eller förlorat innehåll är ganska vanligt. Men gör det inte
Om du har använt pennan eller överstrykningspennan för att rita på dina PowerPoint-bilder under en presentation, kan du spara ritningarna till nästa presentation eller radera dem så att nästa gång du visar den börjar du med rena PowerPoint-bilder. Följ dessa instruktioner för att radera ritningar med penna och överstrykningspenna: Radera linjer ett på […]
Stilbiblioteket innehåller CSS-filer, XSL-filer (Extensible Stylesheet Language) och bilder som används av fördefinierade mallsidor, sidlayouter och kontroller i SharePoint 2010. För att hitta CSS-filer i stilbiblioteket på en publiceringswebbplats: Välj Webbplatsåtgärder→Visa Allt webbplatsinnehåll. Innehållet på webbplatsen visas. Style-biblioteket ligger i […]
Överväldiga inte din publik med gigantiska siffror. I Microsoft Excel kan du förbättra läsbarheten för dina instrumentpaneler och rapporter genom att formatera dina siffror så att de visas i tusentals eller miljoner.
Lär dig hur du använder SharePoints sociala nätverksverktyg som låter individer och grupper kommunicera, samarbeta, dela och ansluta.
Julianska datum används ofta i tillverkningsmiljöer som en tidsstämpel och snabbreferens för ett batchnummer. Denna typ av datumkodning tillåter återförsäljare, konsumenter och serviceagenter att identifiera när en produkt tillverkades och därmed produktens ålder. Julianska datum används också i programmering, militären och astronomi. Annorlunda […]
Du kan skapa en webbapp i Access 2016. Så vad är en webbapp egentligen? Tja, webben betyder att den är online, och appen är bara en förkortning för "applikation". En anpassad webbapp är en onlinedatabasapplikation som nås från molnet med en webbläsare. Du bygger och underhåller webbappen i skrivbordsversionen […]
De flesta sidor i SharePoint 2010 visar en lista med navigeringslänkar i snabbstartsfältet till vänster på sidan. Snabbstartsfältet visar länkar till utvalt webbplatsinnehåll som listor, bibliotek, webbplatser och publiceringssidor. Snabbstartsfältet innehåller två mycket viktiga länkar: Länken Allt webbplatsinnehåll: […]
