Excel 2007s statistiska funktioner – inklusive AVERAGE, MAX, MIN och MEDIAN – finns på en fortsättningsmeny som nås från kommandoknappen Fler funktioners rullgardinsmeny på fliken Formler. Excel innehåller en av de mest kompletta uppsättningarna statistiska funktioner som är tillgängliga utanför ett dedikerat statistikprogram.
Funktionerna AVERAGE, MAX (för max) och MIN (för minimum) är de vanligast använda av de statistiska funktionerna eftersom de är användbara för både den genomsnittliga numeriken och den dedikerade statistikern. Alla tre funktionerna följer samma syntax som den gamla goda SUM-funktionen. Syntaxen för funktionen AVERAGE använder till exempel följande argument, precis som funktionerna SUM, MAX och MIN:
=MEDEL(tal1;[ tal2 ],[...])
Precis som i SUM-funktionen, de siffer argumenten är mellan 1 och 30 numeriska argument som du vill genomsnittet. Bilden nedan illustrerar hur du kan använda funktionerna AVERAGE, MAX, MIN och MEDIAN i ett kalkylblad. Det här exemplet använder dessa funktioner för att beräkna några få statistik över försäljningspriserna för bostäder i ett visst område. Denna statistik omfattar i genomsnitt högst, lägst och median försäljningspriset för bostäder som säljs i april och maj 2008. Alla de statistiska funktioner i detta kalkylblad använder samma antal argument; dvs cellområdet C3:C7. Formlerna som används i detta kalkylblad visas i kolumn D.
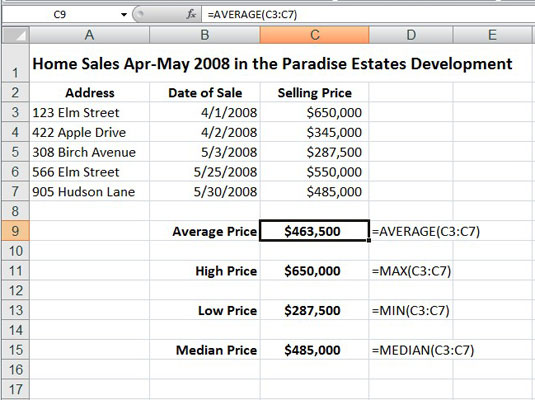
Ett kalkylblad för hemförsäljning som använder vanliga statistiska funktioner.
Funktionen AVERAGE beräknar det aritmetiska medelvärdet av värdena i detta intervall genom att summera dem och sedan dividera dem med antalet värden i intervallet. Denna AVERAGE-funktion motsvarar följande formel:
=SUMMA(C3:C7)/ANTAL(C3:C7)
Observera att den här formeln använder SUM-funktionen för att summera värdena och en annan statistisk funktion som kallas COUNT för att bestämma antalet värden i listan. MAX och MIN funktioner returnerar helt enkelt de högsta och lägsta värdena i cellområdet som används som antalet argument. MEDIAN-funktionen beräknar värdet som ligger i mitten av värdeintervallet; det vill säga den där hälften av värdena är större och hälften är mindre. Detta är anledningen till att medianförsäljningspriset (i cell C15) skiljer sig från det genomsnittliga försäljningspriset (i cell C9) i detta kalkylblad.
Lär dig att använda kommandona Gör om och Upprepa i Word 2016 för att effektivt hantera dina dokument. Dessa funktioner hjälper dig att enkelt ångra och återställa ändringar.
Hur man blockerar Microsoft Word från att öppna filer i skrivskyddat läge på Windows Microsoft Word öppnar filer i skrivskyddat läge, vilket gör det omöjligt att redigera dem? Oroa dig inte, metoderna finns nedan
Så här åtgärdar du fel vid utskrift av felaktiga Microsoft Word-dokument Fel vid utskrift av Word-dokument med ändrade teckensnitt, röriga stycken, saknad text eller förlorat innehåll är ganska vanligt. Men gör det inte
Om du har använt pennan eller överstrykningspennan för att rita på dina PowerPoint-bilder under en presentation, kan du spara ritningarna till nästa presentation eller radera dem så att nästa gång du visar den börjar du med rena PowerPoint-bilder. Följ dessa instruktioner för att radera ritningar med penna och överstrykningspenna: Radera linjer ett på […]
Stilbiblioteket innehåller CSS-filer, XSL-filer (Extensible Stylesheet Language) och bilder som används av fördefinierade mallsidor, sidlayouter och kontroller i SharePoint 2010. För att hitta CSS-filer i stilbiblioteket på en publiceringswebbplats: Välj Webbplatsåtgärder→Visa Allt webbplatsinnehåll. Innehållet på webbplatsen visas. Style-biblioteket ligger i […]
Överväldiga inte din publik med gigantiska siffror. I Microsoft Excel kan du förbättra läsbarheten för dina instrumentpaneler och rapporter genom att formatera dina siffror så att de visas i tusentals eller miljoner.
Lär dig hur du använder SharePoints sociala nätverksverktyg som låter individer och grupper kommunicera, samarbeta, dela och ansluta.
Julianska datum används ofta i tillverkningsmiljöer som en tidsstämpel och snabbreferens för ett batchnummer. Denna typ av datumkodning tillåter återförsäljare, konsumenter och serviceagenter att identifiera när en produkt tillverkades och därmed produktens ålder. Julianska datum används också i programmering, militären och astronomi. Annorlunda […]
Du kan skapa en webbapp i Access 2016. Så vad är en webbapp egentligen? Tja, webben betyder att den är online, och appen är bara en förkortning för "applikation". En anpassad webbapp är en onlinedatabasapplikation som nås från molnet med en webbläsare. Du bygger och underhåller webbappen i skrivbordsversionen […]
De flesta sidor i SharePoint 2010 visar en lista med navigeringslänkar i snabbstartsfältet till vänster på sidan. Snabbstartsfältet visar länkar till utvalt webbplatsinnehåll som listor, bibliotek, webbplatser och publiceringssidor. Snabbstartsfältet innehåller två mycket viktiga länkar: Länken Allt webbplatsinnehåll: […]
