Den hypergeometriska fördelningen handlar om framgångar och misslyckanden och är användbar för statistisk analys med Excel. Låt oss börja med ett exempel. I en uppsättning med 16 glödlampor är 9 bra och 7 är defekta. Om du slumpmässigt väljer 6 glödlampor av dessa 16, vad är sannolikheten att 3 av de 6 är bra? Överväg att välja en bra glödlampa som en "framgång".
När du har valt klart är din uppsättning val en kombination av tre av de nio bra glödlamporna tillsammans med en kombination av tre av de sju defekta glödlamporna. Sannolikheten att få tre bra lökar är en . . . väl. . . kombination av räkneregler.
Varje resultat av valet av de bra glödlamporna kan associeras med alla resultat av valet av de defekta glödlamporna, så produktregeln är lämplig för täljaren. Nämnaren (provutrymmet) är antalet möjliga kombinationer av 6 objekt i en grupp om 16.
HYPGEOM.DIST beräknar allt åt dig när du hanterar den hypergeometriska fördelningen. Så här använder du det för att gå igenom föregående exempel:
Välj en cell för HYPGEOM.DIST:s svar.
Från menyn Statistiska funktioner, välj HYPGEOM.DIST för att öppna dialogrutan Funktionsargument.
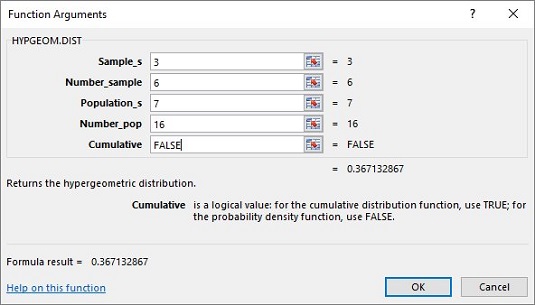
I dialogrutan Funktionsargument anger du lämpliga värden för argumenten.
I rutan Sample_s anger du antalet framgångar i provet. Den siffran är 3 för det här exemplet.
I rutan Number_sample anger du antalet artiklar i provet. Urvalsstorleken för detta exempel är 6.
I rutan Population_s anger du antalet framgångar i populationen. I det här exemplet är det 7, antalet bra glödlampor.
I rutan Number_pop anger du antalet objekt i populationen. Det totala antalet glödlampor är 16, och det är befolkningens storlek.
I rutan Kumulativ anger du FALSK. Detta ger sannolikheten för antalet framgångar du angett i rutan Sample_s. Om du anger TRUE returnerar funktionen sannolikheten för högst det antalet framgångar (till exempel den kumulativa sannolikheten).
Med värden angivna för alla argument visas svaret i dialogrutan. Svaret är 0,367 och ytterligare några decimaler. Klicka på OK för att placera svaret i den markerade cellen.
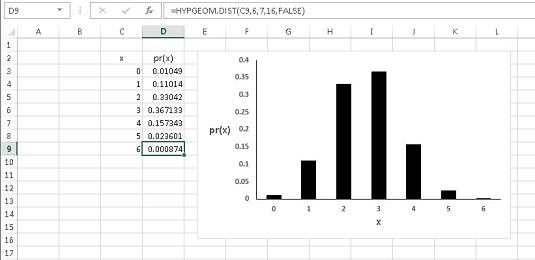
Du kan använda HYP.GEOM.DIST för att beräkna pr (0) till pr (6) för detta exempel. Sedan använder du Excels grafikfunktioner för att plotta resultaten. Målet är att hjälpa dig att visualisera och förstå den hypergeometriska fördelningen.
Hur man blockerar Microsoft Word från att öppna filer i skrivskyddat läge på Windows Microsoft Word öppnar filer i skrivskyddat läge, vilket gör det omöjligt att redigera dem? Oroa dig inte, metoderna finns nedan
Så här åtgärdar du fel vid utskrift av felaktiga Microsoft Word-dokument Fel vid utskrift av Word-dokument med ändrade teckensnitt, röriga stycken, saknad text eller förlorat innehåll är ganska vanligt. Men gör det inte
Om du har använt pennan eller överstrykningspennan för att rita på dina PowerPoint-bilder under en presentation, kan du spara ritningarna till nästa presentation eller radera dem så att nästa gång du visar den börjar du med rena PowerPoint-bilder. Följ dessa instruktioner för att radera ritningar med penna och överstrykningspenna: Radera linjer ett på […]
Stilbiblioteket innehåller CSS-filer, XSL-filer (Extensible Stylesheet Language) och bilder som används av fördefinierade mallsidor, sidlayouter och kontroller i SharePoint 2010. För att hitta CSS-filer i stilbiblioteket på en publiceringswebbplats: Välj Webbplatsåtgärder→Visa Allt webbplatsinnehåll. Innehållet på webbplatsen visas. Style-biblioteket ligger i […]
Överväldiga inte din publik med gigantiska siffror. I Microsoft Excel kan du förbättra läsbarheten för dina instrumentpaneler och rapporter genom att formatera dina siffror så att de visas i tusentals eller miljoner.
Lär dig hur du använder SharePoints sociala nätverksverktyg som låter individer och grupper kommunicera, samarbeta, dela och ansluta.
Julianska datum används ofta i tillverkningsmiljöer som en tidsstämpel och snabbreferens för ett batchnummer. Denna typ av datumkodning tillåter återförsäljare, konsumenter och serviceagenter att identifiera när en produkt tillverkades och därmed produktens ålder. Julianska datum används också i programmering, militären och astronomi. Annorlunda […]
Du kan skapa en webbapp i Access 2016. Så vad är en webbapp egentligen? Tja, webben betyder att den är online, och appen är bara en förkortning för "applikation". En anpassad webbapp är en onlinedatabasapplikation som nås från molnet med en webbläsare. Du bygger och underhåller webbappen i skrivbordsversionen […]
De flesta sidor i SharePoint 2010 visar en lista med navigeringslänkar i snabbstartsfältet till vänster på sidan. Snabbstartsfältet visar länkar till utvalt webbplatsinnehåll som listor, bibliotek, webbplatser och publiceringssidor. Snabbstartsfältet innehåller två mycket viktiga länkar: Länken Allt webbplatsinnehåll: […]
För enkla problem hittar Solver i Excel vanligtvis snabbt de optimala Solver-variabelvärdena för objektivfunktionen. Men i vissa fall har Solver problem med att hitta Solver-variabelvärdena som optimerar objektivfunktionen. I dessa fall visar Solver vanligtvis ett meddelande eller ett felmeddelande som beskriver eller diskuterar problemet som […]
