Excel är ett underbart verktyg när du behöver använda statistik. Om du aldrig har varit utsatt för statistik i skolan eller om det har gått ett eller två decennier sedan du var, låt dessa tips hjälpa dig att använda några av de statistiska verktyg som Excel tillhandahåller.
Det första du borde veta är att viss statistisk analys och vissa statistiska mått är ganska enkla. Beskrivande statistik, som inkluderar saker som pivottabellernas korstabeller, såväl som några av de statistiska funktionerna, är meningsfull även för någon som inte är så kvantitativ.
När någon använder begreppet medelvärde är det han brukar syfta på det vanligaste medelmåttet, vilket är ett medelvärde. Att förstå att termen genomsnitt är oprecis gör mycket av Excels statistiska funktionalitet mer begriplig.
För att göra denna diskussion mer konkret, anta att du tittar på en liten uppsättning värden: 1, 2, 3, 4 och 5. Som du kanske vet är medelvärdet i denna lilla uppsättning värden 3. Du kan räkna ut medelvärdet genom att lägga ihop alla siffror i mängden (1+2+3+4+5) och sedan dividera denna summa (15) med det totala antalet värden i mängden (5).
Den medianvärdet är det värde som skiljer de största värdena från de minsta värdena. I datamängden 1, 2, 3, 4 och 5 är medianen 3. Värdet 3 skiljer de största värdena (4 och 5) från de minsta värdena (1 och 2).
Du behöver inte förstå olika mätningar under i genomsnitt, men du bör komma ihåg att termen genomsnitt är ganska oprecis.
Formeln för standardavvikelse och logiken är ganska lätt att förstå.
En standardavvikelse beskriver hur värden i en datamängd varierar runt medelvärdet. Det snygga med statistiska mått som en standardavvikelse, du får ofta verkliga insikter i egenskaperna hos den data du tittar på. En annan sak är att med dessa två databitar kan du ofta dra slutsatser om data genom att titta på prover.
Observation är en av termerna som du kommer att stöta på om du läser något om statistik. En observation är bara en observation. Ett sätt att definiera termen observation är så här: När du faktiskt tilldelar ett värde till en av dina slumpvariabler skapar du en observation.
Ett urval är en samling observationer från en population. Till exempel, om du skapar en datamängd som registrerar den dagliga höga temperaturen i ditt grannskap, är din lilla samling observationer ett exempel.
I jämförelse är ett urval inte en population. En population inkluderar alla möjliga observationer.
Om man tittar på ett urval av värden från en population och urvalet är representativt och tillräckligt stort, kan man dra slutsatser om populationen utifrån egenskaper hos urvalet.
Slutsatsstatistik, även om den är mycket kraftfull, har två egenskaper som du behöver känna till:
Noggrannhetsproblem
Brant inlärningskurva
P robability fördelningsfunktionen låter ganska knepigt; men du kan faktiskt intuitivt förstå vad en sannolikhetsfördelningsfunktion är med ett par användbara exempel.
En vanlig fördelning som man till exempel hör talas om i statistikklasser är en T-fördelning. En T-fördelning är i huvudsak en normalfördelning förutom med tyngre, fetare svansar.
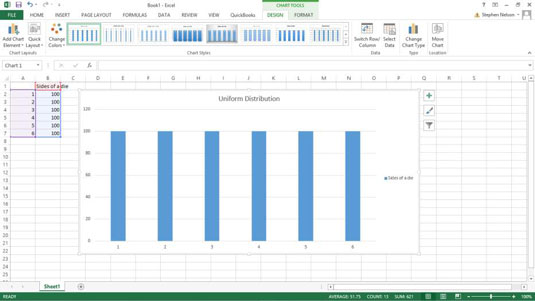
En vanlig sannolikhetsfördelningsfunktion är en enhetlig fördelning. I en enhetlig fördelning har varje händelse samma sannolikhet att inträffa. Det unika med den här distributionen är att allt är ganska jämnt.
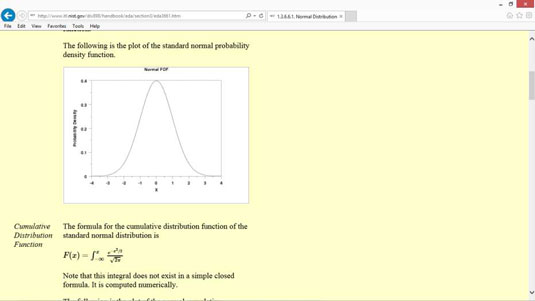
En annan vanlig typ av sannolikhetsfördelningsfunktion är normalfördelningen, även känd som en klockkurva eller en Gaussfördelning.
En normalfördelning sker naturligt i många situationer. Till exempel är intelligenskvoter (IQ) normalfördelade.
En parameter är en indata till sannolikhetsfördelningsfunktionen. Med andra ord behöver formeln eller funktionen eller ekvationen som beskriver en sannolikhetsfördelningskurva indata. I statistiken kallas dessa indata parametrar.
Vissa sannolikhetsfördelningsfunktioner behöver bara en enda enkel parameter. För att till exempel arbeta med en enhetlig fördelning behöver du egentligen bara antalet värden i datamängden. En sexsidig tärning, till exempel, har bara sex möjligheter.
Ett par andra användbara statistiska termer att känna till är skevhet och kurtosis. Skevhet kvantifierar bristen på symmetri i en sannolikhetsfördelning. I en perfekt symmetrisk fördelning, som normalfördelningen, är skevheten lika med noll. Om en sannolikhetsfördelning lutar åt höger eller vänster är dock skevheten lika med något annat värde än noll, och värdet kvantifierar bristen på symmetri.
Kurtosis kvantifierar svansarnas tyngd i en fördelning. I en normalfördelning är kurtosis lika med noll. Den Svansen är det som når ut till vänster eller höger. Men om en svans i en fördelning är tyngre än en normalfördelning är kurtosen ett positivt tal. Om svansarna i en fördelning är smalare än i en normalfördelning är kurtosen ett negativt tal.
Sannolikheter förvirrar ofta människor. En viktig sak att förstå om konfidensnivåer är att de är kopplade till felmarginalen.
En annan viktig sak att förstå om konfidensnivåer är att ju större du gör ditt urval, desto mindre kommer din felmarginal att använda samma konfidensnivå.
Som bara ett exempel, säg att du hade lite Google Analytics-data om två olika webbannonser som du kör för att marknadsföra ditt småföretag, och du vill veta vilken annons som är mer effektiv. Du kan använda konfidensintervallsformeln för att ta reda på hur länge dina annonser behöver visas innan Google har samlat in tillräckligt med data för att du ska veta vilken annons som verkligen är bättre.
Lär dig att använda kommandona Gör om och Upprepa i Word 2016 för att effektivt hantera dina dokument. Dessa funktioner hjälper dig att enkelt ångra och återställa ändringar.
Hur man blockerar Microsoft Word från att öppna filer i skrivskyddat läge på Windows Microsoft Word öppnar filer i skrivskyddat läge, vilket gör det omöjligt att redigera dem? Oroa dig inte, metoderna finns nedan
Så här åtgärdar du fel vid utskrift av felaktiga Microsoft Word-dokument Fel vid utskrift av Word-dokument med ändrade teckensnitt, röriga stycken, saknad text eller förlorat innehåll är ganska vanligt. Men gör det inte
Om du har använt pennan eller överstrykningspennan för att rita på dina PowerPoint-bilder under en presentation, kan du spara ritningarna till nästa presentation eller radera dem så att nästa gång du visar den börjar du med rena PowerPoint-bilder. Följ dessa instruktioner för att radera ritningar med penna och överstrykningspenna: Radera linjer ett på […]
Stilbiblioteket innehåller CSS-filer, XSL-filer (Extensible Stylesheet Language) och bilder som används av fördefinierade mallsidor, sidlayouter och kontroller i SharePoint 2010. För att hitta CSS-filer i stilbiblioteket på en publiceringswebbplats: Välj Webbplatsåtgärder→Visa Allt webbplatsinnehåll. Innehållet på webbplatsen visas. Style-biblioteket ligger i […]
Överväldiga inte din publik med gigantiska siffror. I Microsoft Excel kan du förbättra läsbarheten för dina instrumentpaneler och rapporter genom att formatera dina siffror så att de visas i tusentals eller miljoner.
Lär dig hur du använder SharePoints sociala nätverksverktyg som låter individer och grupper kommunicera, samarbeta, dela och ansluta.
Julianska datum används ofta i tillverkningsmiljöer som en tidsstämpel och snabbreferens för ett batchnummer. Denna typ av datumkodning tillåter återförsäljare, konsumenter och serviceagenter att identifiera när en produkt tillverkades och därmed produktens ålder. Julianska datum används också i programmering, militären och astronomi. Annorlunda […]
Du kan skapa en webbapp i Access 2016. Så vad är en webbapp egentligen? Tja, webben betyder att den är online, och appen är bara en förkortning för "applikation". En anpassad webbapp är en onlinedatabasapplikation som nås från molnet med en webbläsare. Du bygger och underhåller webbappen i skrivbordsversionen […]
De flesta sidor i SharePoint 2010 visar en lista med navigeringslänkar i snabbstartsfältet till vänster på sidan. Snabbstartsfältet visar länkar till utvalt webbplatsinnehåll som listor, bibliotek, webbplatser och publiceringssidor. Snabbstartsfältet innehåller två mycket viktiga länkar: Länken Allt webbplatsinnehåll: […]
