Како користити ПВ, НПВ и ФВ функције у програму Екцел 2016

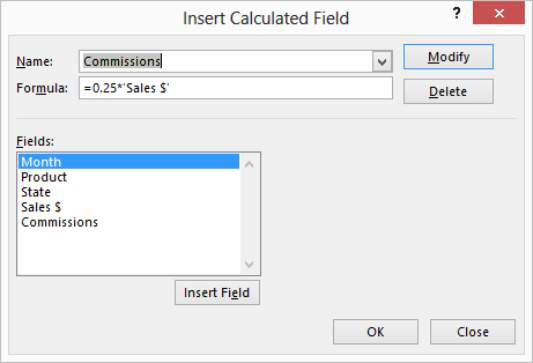
Функције ПВ (садашња вредност), НПВ (нето садашња вредност) и ФВ (будућа вредност) у програму Екцел 2016 које се налазе у падајућем менију дугмета Финансијски на картици Формуле траке (Алт+МИ) вам омогућавају да одредите профитабилност инвестиције.

Израчунавање садашње вредности

Функција ПВ, или садашња вредност, враћа садашњу вредност инвестиције, што је укупан износ који серија будућих плаћања тренутно вреди. Синтакса ПВ функције је следећа:

=ПВ(стопа,нпер,пмт,[фв],[тип])

У Фв и тип аргументи су опциони аргументи у функцији (означен средњим заградама). ФВ аргумент је вредност будућност или стање готовине коју желите да имате након што последњу уплату. Ако изоставите аргумент фв , Екцел претпоставља будућу вредност нула (0). Тип Аргумент показује да ли се плаћање врши на почетку или на крају периода: унесите 0 (или изоставите типа аргумент) када се плаћање врши на крају периода, и користи 1 када је направљен на почетку тачка.

Следећа слика садржи неколико примера коришћења ПВ функције. Све три ПВ функције користе исту годишњу процентуалну стопу од 1,25 посто и рок од 10 година. Пошто се плаћања врше месечно, свака функција претвара ове годишње бројке у месечне. На пример, у ПВ функцији у ћелији Е3, годишња каматна стопа у ћелији А3 се претвара у месечну стопу дељењем са 12 (А3/12). Годишњи рок у ћелији Б3 се претвара у еквивалентне месечне периоде множењем са 12 (Б3 к 12).

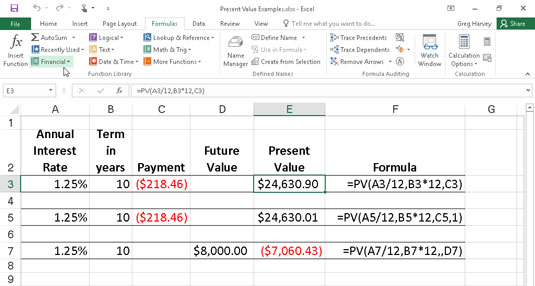
Коришћење ПВ функције за израчунавање садашње вредности различитих инвестиција.

Имајте на уму да иако ПВ функције у ћелијама Е3 и Е5 користе аргументе рате, нпер и пмт (218,46 УСД), њихови резултати су мало другачији. Ово је узроковано разликом у аргументу типа у две функције: ПВ функција у ћелији Е3 претпоставља да се свака уплата врши на крају периода ( аргумент типа је 0 кад год се изостави), док ПВ функција у целл Е5 подразумева да свака уплата врши на почетку периода (коју показује типу аргументу 1). Када се плаћање изврши на почетку периода, садашња вредност ове инвестиције је 0,89 долара виша него када се плаћање изврши на крају периода, одражавајући камату обрачунату током последњег периода.

Трећи пример у ћелији Е7 (приказан на слици 4-1) користи функцију ПВ са аргументом фв уместо аргумента пмт . У овом примеру, функција ПВ наводи да бисте морали да плаћате месечно од 7.060,43 долара за период од 10 година да бисте остварили готовински салдо од 8.000 долара, под претпоставком да је инвестиција вратила константну годишњу каматну стопу од 1 1/4 процента. Имајте на уму да када користите функцију ПВ са аргументом фв уместо аргументом пмт , и даље морате да наведете позицију пмт аргумента у функцији зарезом (дакле, две зарезе у реду у функцији) тако да Екцел не Немојте погрешити свој фв аргумент са аргументом пмт .

Израчунавање нето садашње вредности

Функција НПВ израчунава нето садашњу вредност на основу низа новчаних токова. Синтакса ове функције је

=НПВ( стопа , вредност1 ,[ вредност2 ],[...])

где су вредност1, вредност2 и тако даље између 1 и 13 аргумената вредности који представљају низ уплата (негативне вредности) и прихода (позитивне вредности), од којих је сваки на једнаком временском размаку и јавља се на крају периода. Инвестиција НПВ почиње један период пре периода тока готовине вредности1 и завршава се последњим новчаним током на листи аргумената. Ако се ваш први новчани ток деси на почетку периода, морате га додати резултату функције НПВ уместо да га укључите као један од аргумената.

Следећа слика илуструје употребу функције НПВ за процену атрактивности петогодишње инвестиције која захтева почетно улагање од 30.000 долара (вредност у ћелији Г3). Прве године очекујете губитак од 22.000 долара (ћелија Б3); друге године, профит од 15.000 долара (ћелија Ц3); трећа година, профит од 25.000 долара (ћелија Д3); четврта година, профит од 32.000 долара (ћелија Е3); и пете године, профит од 38.000 долара (ћелија Ф3). Имајте на уму да се ове референце ћелија користе као аргументи вредности функције НПВ.

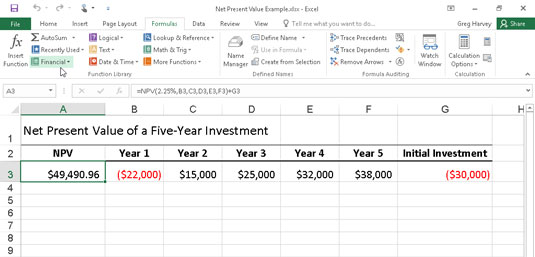
Коришћење функције НПВ за израчунавање нето садашње вредности инвестиције.

За разлику од коришћења ПВ функције, НПВ функција не захтева равномеран ток новчаних токова. Стопа аргумент у функцији је постављена на 2,25 одсто. У овом примеру, ово представља дисконтну стопу инвестиције — односно каматну стопу коју можете очекивати да ћете добити током петогодишњег периода ако свој новац уложите у неку другу врсту улагања, као што је новац са високим приносом -тржишни рачун. Ова функција НПВ у ћелији А3 враћа нето садашњу вредност од 49.490,96 долара, што указује да можете очекивати да ћете остварити много више од улагања својих 30.000 долара у ову инвестицију него што бисте могли да уложите новац на рачун тржишта новца по каматној стопи од 2,25 одсто.

Израчунавање будуће вредности

ФВ функција израчунава будућу вредност инвестиције. Синтакса ове функције је

=ФВ(стопа,нпер,пмт,[пв],[тип])

Тхе стопа, НПЕР, ПМТ, а тип аргументи су исти као они користе функције ПВ. ПВ аргумент је садашња вредност или паушално износ за који желите да израчунате вредности будуће. Као и код аргумената фв и типа у функцији ПВ, и пв и аргументи типа су опциони у функцији ФВ. Ако изоставите ове аргументе, Екцел претпоставља да су њихове вредности нула (0) у функцији.

Можете користити ФВ функцију да израчунате будућу вредност инвестиције, као што је ИРА (Индивидуални пензиони рачун). На пример, претпоставимо да сте основали ИРА са 43 године и да ћете се пензионисати за 22 године са 65 година и да планирате да извршите годишње уплате у ИРА на почетку сваке године. Ако претпоставите стопу приноса од 2,5 одсто годишње, у радни лист бисте унели следећу ФВ функцију:

=ФВ(2,5%,22,–1500,,1)

Екцел затим указује да можете очекивати будућу вредност од 44.376,64 долара за своју ИРА када се пензионишете са 65 година. Ако сте успоставили ИРА годину дана раније и рачун већ има садашњу вредност од 1.538 долара, променили бисте ФВ функцију на следећи начин :

=ФВ(2,5%,22,–1500,–1538,1)

У овом случају, Екцел указује да можете очекивати будућу вредност од 47.024,42 долара за вашу ИРА при пензионисању.