Sammenkoblede prøver T-Test i Excel

I denne opplæringen lærer du hvordan du utfører og tolker den sammenkoblede t-testen ved hjelp av Excel. Du kan se hele videoen av denne opplæringen nederst på denne bloggen .

Den sammenkoblede t-testen skal se etter en forskjell i middelverdiene for observasjoner. Så vi har å gjøre med kvantitative data mellom en tidsperiode og en annen. Vi har også å gjøre med tidsseriedata.

Dette kommer til å være en hypotesetest med alle beslagene som følger med det. Hvis du vil lære mer om hvordan du gjør en hypotesetest i Excel, kan du sjekke ut boken min Advancing Into Analytics .

Vi skal ikke gå for mye inn i teorien, men vi skal bruke analyseverktøypakken i Excel, der vi skal teste på 95 % signifikansnivå og bruke et fagfellevurdert datasett fra Plos One .

I bunn og grunn, det vi ønsker å finne er om det er en forskjell i middelverdien for gruppe 1 mellom tid 1 og tid 2. Vi skal prøve å reprodusere en forskningsstudie.

Innholdsfortegnelse

• Utføre og tolke sammenkoblede prøver T-test
• Konklusjon

Utføre og tolke sammenkoblede prøver T-test

La oss gå videre og dykke ned i . Vi kan kjøre dette per prøvetest, og så omgrupperer vi og går derfra.

I disse dataene er dette enkeltpasienter. De ble målt i en periode kalt Volum 1 og deretter gitt en annen måling i Volum 2 .

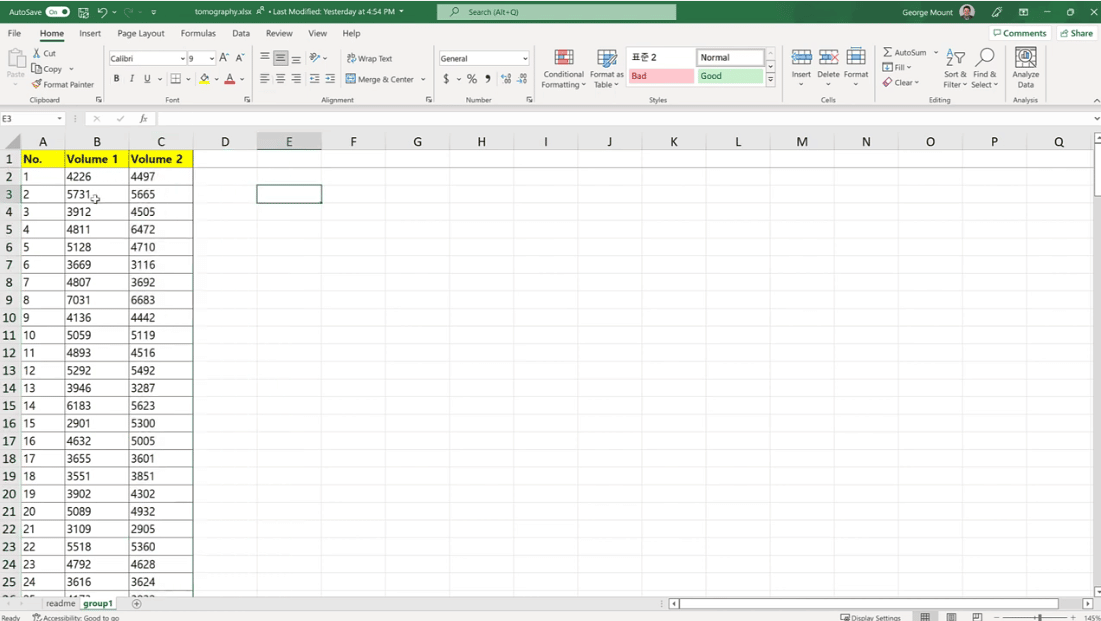
Vi må kjenne til målingene i begge periodene ellers kan vi ikke bruke disse pasientene eller disse observasjonene. Det er én ting å vite om t-testen for sammenkoblede prøver.

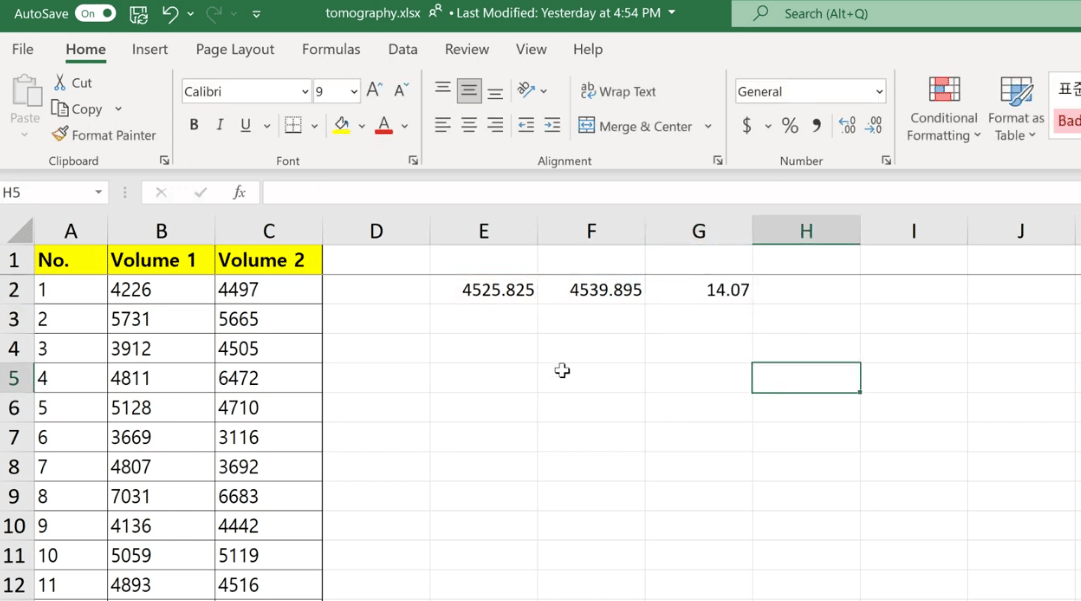
La oss ta gjennomsnittet av bind 1 og bind 2 data og deretter få forskjellen mellom de to. Det ser ut til at bind 2 er litt høyere med 14.07.

Det fine med å bruke hypotesetesting er at vi virkelig kan grave i dette og avgjøre om det vi ser bare er et lykketreff eller ikke.

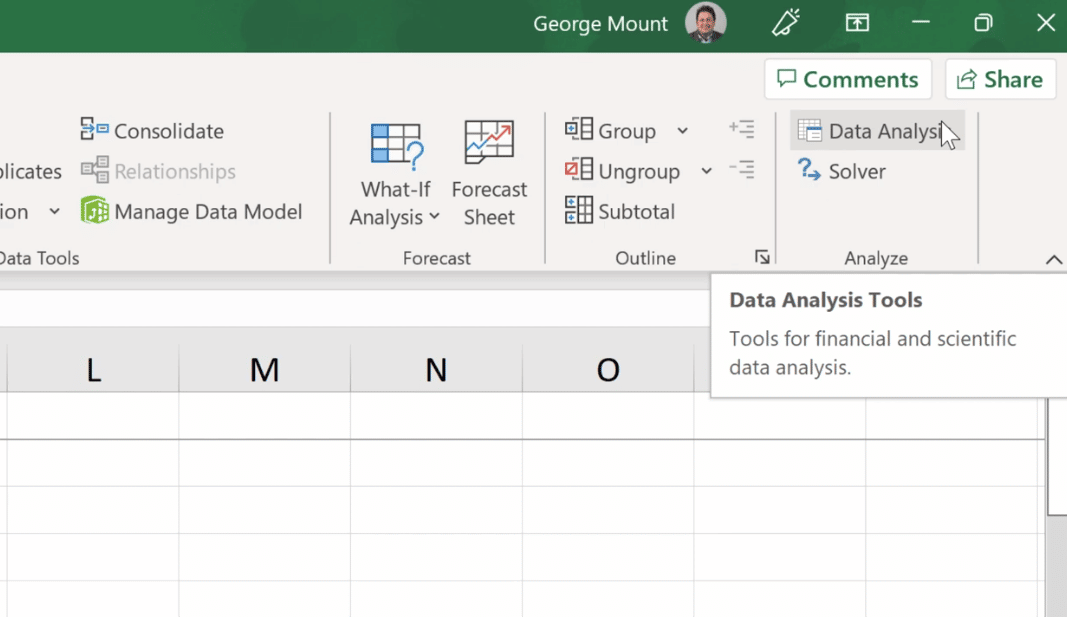
Den neste tingen å gjøre er å gå til Data- delen og deretter velge Data Analysis Tools . Hvis du ikke er kjent med verktøypakken, kan du sjekke ut boken for å lære hvordan du installerer den eller foreta et nettsøk.

Fra alternativene, velg t-Test: Paret to prøve for midler og klikk deretter på OK- knappen.

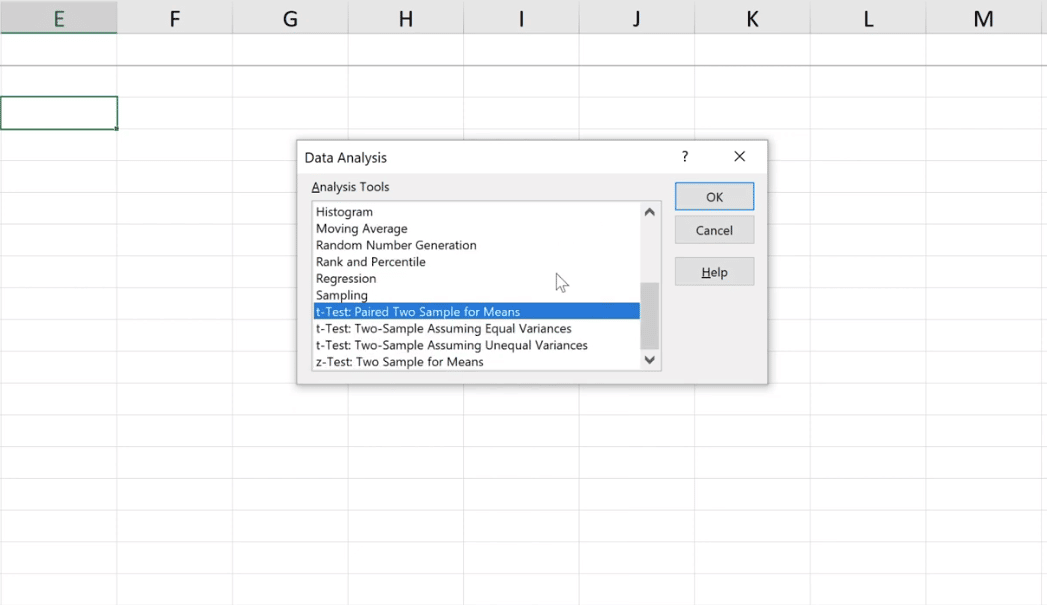
For dette vinduet må vi angi to områder.

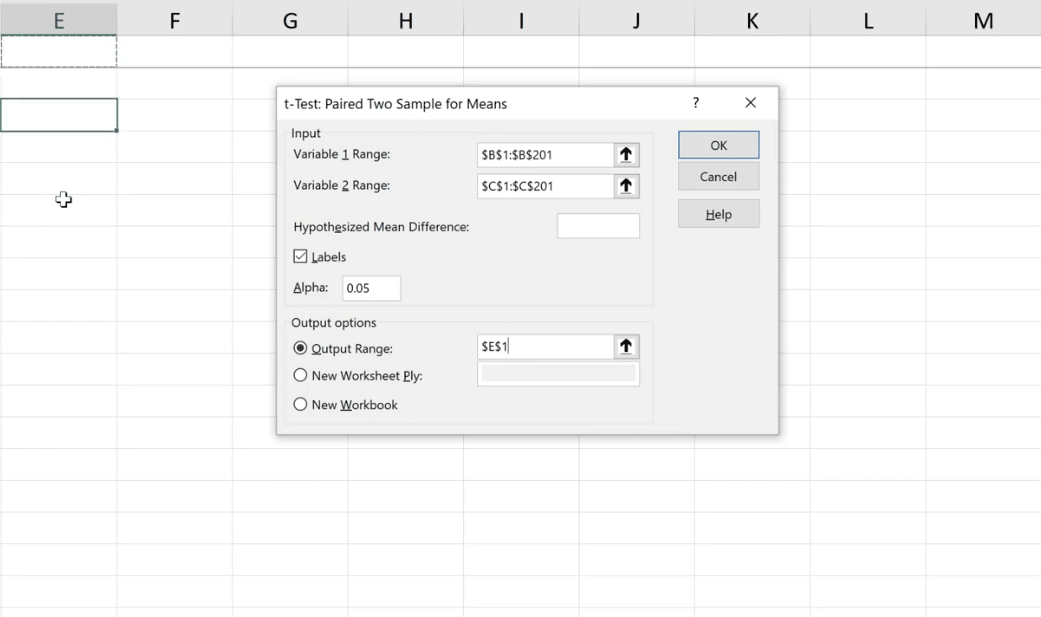
For Variable 1 Range , velg hele området av Volume 1-data ved å trykke CTRL+Shift+pil ned . La oss også velge hele området for Volum 2 for Variable 2 Range- feltet.

Vi fikk samme antall observasjoner i hver gruppe, noe som er fornuftig fordi vi trenger disse observasjonene for hver pasient.

Siden vi har etiketter i den første raden, la oss merke av for Etiketter , og la den stå tom for Hypotesisert gjennomsnittsforskjell . Det kommer til å anta at gjennomsnittsforskjellen er vesentlig forskjellig fra null. Vi kan også sjekke om det er annerledes enn 5 eller -10, men 0 er det vanligste.

For Output Range kan vi legge dette i samme regneark og deretter klikke OK .

Merkbart at dette er en veldig menydrevet tilnærming for å finne forskjellen på denne testen. Vi kan se de samme tallene som vi gjorde tidligere.

Deretter vil jeg at du skal fokusere oppmerksomheten på P(T<=t)>- verdien, som er 0,751 . Det betyr at det sannsynligvis ikke er en signifikant forskjell selv om dette tallet er litt høyere statistisk sett. Vi kan ikke si at det sannsynligvis er annerledes enn 0.

Igjen er målet å ta analysen din til neste nivå ved å bruke hypotesetesting på den.

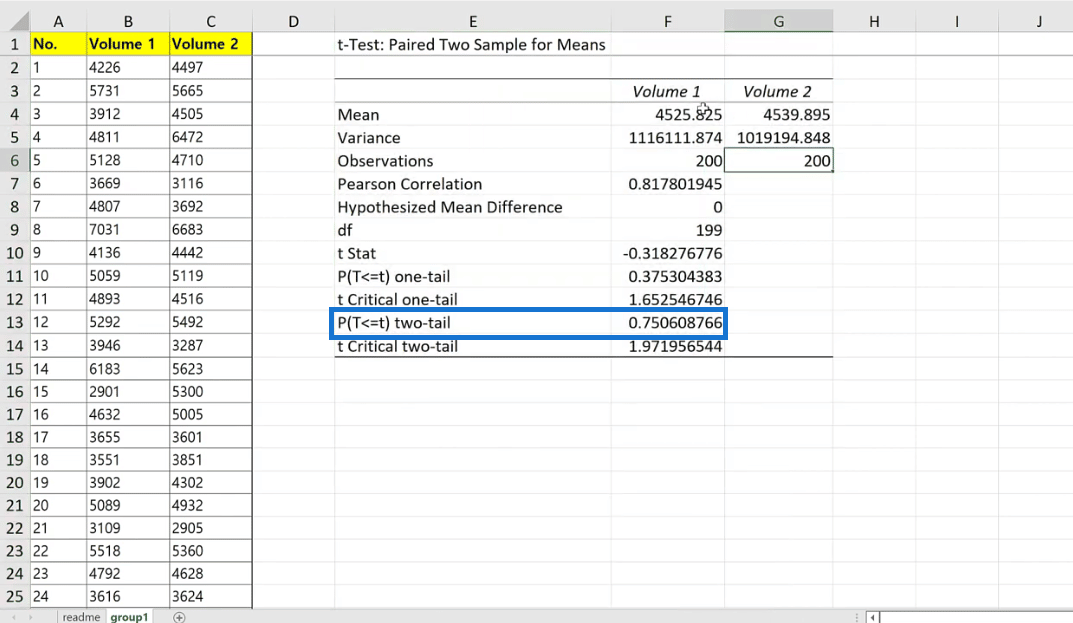
Til slutt, la oss sjekke ut dataene for gruppe 1.

Basert på tabellen kan vi se fra Plos One Journal at p-verdien er 0,751. Dette betyr at vi klarte å reprodusere forskningsresultatene fra denne rapporten, noe som er kjempebra!

Kudos til forskerne også for å ha publisert dataene deres og gjort tilgjengelig for offentligheten slik at alle kan få tilgang til dette. 

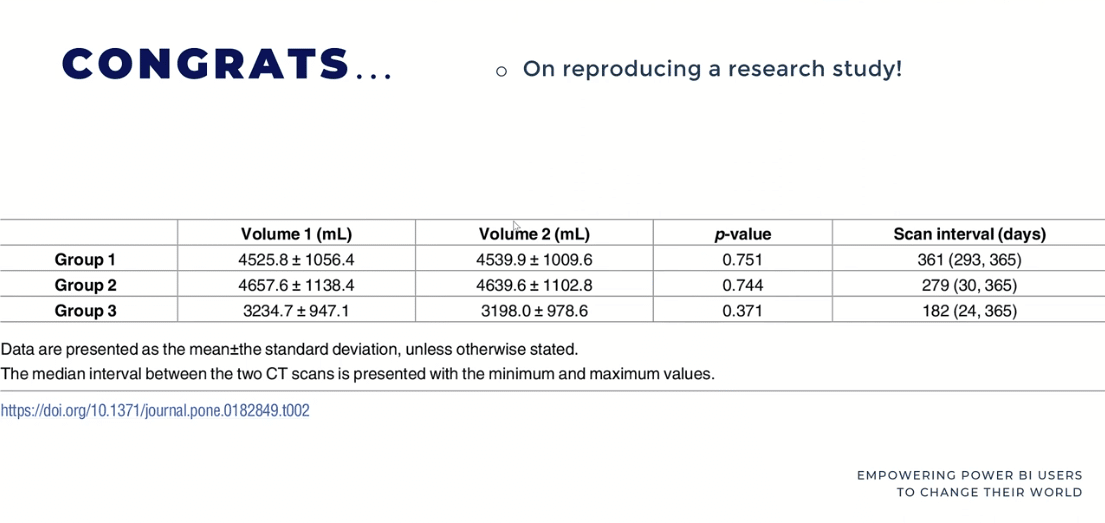
Oftest brukes den sammenkoblede t-testen når det er en intervensjon, enten det er innen medisin, markedsføring eller utdanning. Derfor er dette ofte en samfunnsvitenskapelig test for å bruke og vite om det har vært noen endring gitt i intervensjon.

Den vanskelige siden av det er imidlertid at vi trenger å ha observasjoner for både før- og etterintervensjon, noe som er vanskelig å gjøre ofte i forretningssammenheng.

Konklusjon

En t-test for parvise prøver er en statistisk prosedyre som brukes til å sammenligne gjennomsnittet for to relaterte grupper eller prøver. Det brukes ofte i situasjoner der du har to relaterte prøver som du vil sammenligne.

Dette gjør det til et tilgjengelig og praktisk verktøy for forskere og analytikere som trenger å raskt og nøyaktig sammenligne midlene til to relaterte grupper.

Totalt sett er dette et viktig verktøy for alle som jobber med data og søker å trekke meningsfulle konklusjoner fra dem.

Beste ønsker,

George Mount