Hvordan normalisere NumPy-matriser: En hurtigveiledning

Hvis du har jobbet med Python for dataanalyse eller maskinlæring, har du sannsynligvis kommet over NumPy-matriser. De er et kraftig verktøy for å håndtere numeriske data, men noen ganger må dataene i disse matrisene justeres eller "normaliseres" for å bli effektivt brukt i algoritmene dine. Men hva betyr det å normalisere en matrise?

For å normalisere en NumPy-matrise, må du justere verdiene i matrisen slik at de faller innenfor et visst område, typisk mellom 0 og 1, eller slik at de har en standard normalfordeling med et gjennomsnitt på 0 og et standardavvik på 1 Dette gjøres ofte innen maskinlæring og dataanalyse for å sikre at alle inndatafunksjoner har samme skala.

I denne artikkelen skal vi utforske hvordan du kan normalisere en NumPy-matrise i Python. Vi skal se på de forskjellige metodene du kan bruke for å normalisere en NumPy-matrise og også se på eksempler for å hjelpe deg å forstå konseptet bedre.

La oss komme inn i det!

Innholdsfortegnelse

• Hva er det grunnleggende om normalisering i Python?
  • Hva er normalisering?
  • Hvorfor er normalisering viktig?
  • Hva er normer?
  • Hva er normalisering i maskinlæring?
• Hva er teknikkene for normalisering i Python?
  • 1. Hvordan utføre Min-Max-skalering
  • 2. Hvordan utføre L1-normalisering
  • 3. Hvordan utføre L2-normalisering
• Hvordan bruke Scikit-Learn for normalisering i Python
  • 1. Hvordan normalisere array ved hjelp av MinMaxScaler
  • 2. Hvordan utføre radnormalisering på stedet
• Siste tanker

Hva er det grunnleggende om normalisering i Python?

Før vi implementerer normalisering i Python, må du forstå hva normalisering betyr.

Derfor vil vi i denne delen gå gjennom hva som er normalisering og dets kjernekonsepter.

Hva er normalisering?

Normalisering er en prosess som skalerer og transformerer data til et standardisert område. Dette gjøres ved å dele hvert element i dataene med en parameter. Parameteren kan være maksimumsverdien, området eller en annen norm.

Du kan normalisere NumPy-matrisen ved å bruke den euklidiske normen (også kjent som L2-normen). Videre kan du også normalisere NumPy-matriser ved å skalere verdiene mellom et visst område, vanligvis 0 til 1.

I Python gir NumPy-biblioteket en effektiv måte å normalisere arrays på. Dette inkluderer også flerdimensjonale matriser og matriser.

Hvorfor er normalisering viktig?

Normalisering er viktig da det sikrer at ulike funksjoner behandles likt når man sammenligner og analyserer data. Du kan bruke den til å eliminere potensielle skjevheter eller avvik som kan oppstå på grunn av varierende skalaer.

Hva er normer?

Parameteren du bruker for normalisering kan være forskjellige normer , for eksempel den euklidiske normen (L2), Manhattan-normen (L1) eller maksnormen (L_inf). Du bruker normer for å beregne størrelsen på en vektor eller matrise . Disse brukes så som en skaleringsfaktor for å normalisere dataene.

Når vi jobber med matriser bruker vi ofte Frobenius-normen , som er en generalisering av den euklidiske normen for flerdimensjonale arrays.

Følgende eksempel viser normaliseringen av en matrise ved hjelp av Frobenius-normen:

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Calculate the Frobenius norm
frobenius_norm = np.linalg.norm(matrix, 'fro')

# Normalize the matrix
normalized_matrix = matrix / frobenius_norm

print('Original Matrix:')
print(matrix)
print('nFrobenius Norm:')
print(frobenius_norm)
print('nNormalized Matrix:')
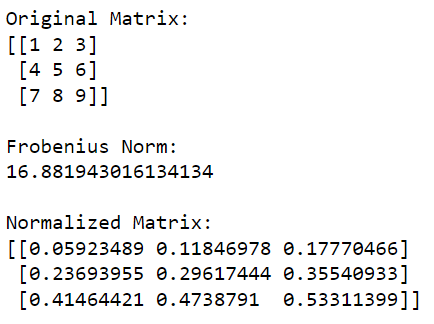
print(normalized_matrix)

Denne Python-koden vil først importere NumPy-biblioteket og bruke det til å lage en matrise. Den beregner deretter Frobenius-normen til matrisen og deler deretter hvert element i matrisen med denne verdien for å normalisere den.

Utgangen av denne koden er gitt nedenfor:

Hva er normalisering i maskinlæring?

I maskinlæring er normalisering et viktig forbehandlingstrinn da det forbedrer ytelsen til algoritmer.

Når du utfører gradientbaserte optimaliseringsteknikker, vil du oppdage at optimaliserte funksjoner har en tendens til å konvergere raskere og mer effektivt. Dette er fordi det reduserer risikoen for dårlig skalering eller forsvinnende gradienter.

Hva er teknikkene for normalisering i Python?

Du kan utføre normalisering av matriser på en rekke måter. Noen metoder er imidlertid mer populære enn andre på grunn av deres høye effektivitet.

For denne delen skal vi se på de tre mye brukte normaliseringsteknikkene:

1. Min-maks skalering

2. L1 Normalisering

3. L2 Normalisering

1. Hvordan utføre Min-Max-skalering

Min-maks-skalering er også kjent som lineær normalisering eller funksjonsskalering. I min-maks-skalering skalerer vi verdiene til en NumPy-matrise slik at de faller innenfor et spesifisert område, vanligvis mellom 0 og 1.

For å gjøre dette trekker du minimumsverdien fra hvert element og deler resultatet med differansen mellom maksimums- og minimumsverdiene.

Du kan representere min-maks-skaleringen matematisk som:

x' = (x - min(x)) / (max(x) - min(x))

Følgende eksempel viser hvordan du kan utføre min-maks-skalering ved å bruke NumPy-biblioteket:

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform min-max scaling
min_val = np.min(matrix)
max_val = np.max(matrix)

scaled_matrix = (matrix - min_val) / (max_val - min_val)

print('Original Matrix:')
print(matrix)
print('nMin-Max Scaled Matrix:')
print(scaled_matrix)

Denne koden vil først importere NumPy og deretter beregne minimums- og maksimumsverdiene i matrisen, som den deretter skalerer slik at alle verdiene er mellom 0 (tilsvarer den opprinnelige minimumsverdien) og 1 (tilsvarer den opprinnelige maksimumsverdien).

Utgangen av denne koden er gitt nedenfor:

Min-maks-skalering er en veldig vanlig form for skalering innen maskinlæring og dataforbehandling.

2. Hvordan utføre L1-normalisering

L1-normalisering bruker L1-normen, som er summen av de absolutte verdiene til matriseelementene. Dette er spesielt nyttig for sparsomme matriser. Det sikrer at summen av de absolutte verdiene til de normaliserte matriseelementene er lik 1.

Formelen for L1 normalisering er:

x' = x / sum(|x|)

Følgende eksempel viser hvordan du kan utføre L1-normalisering ved å bruke NumPy:

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform L1 normalization
l1_norm = np.linalg.norm(matrix, 1, axis=1, keepdims=True)
l1_normalized_matrix = matrix / l1_norm

print('Original Matrix:')
print(matrix)
print('nL1 Normalized Matrix:')
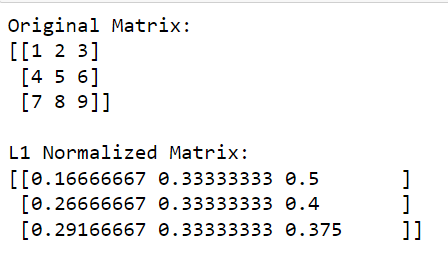
print(l1_normalized_matrix)

I denne koden beregner np.linalg.norm (matrise, 1, akse=1, keepdims=True) L1-normen for hver rad (dette gjøres ved å spesifisere akse=1).

Denne operasjonen vil returnere en kolonnevektor der hvert element er L1-normen til den tilsvarende raden. Ved å dele den opprinnelige matrisen med disse normene (utføre delingen element-vis), får vi den L1 normaliserte versjonen av matrisen.

Utgangen er gitt nedenfor:

3. Hvordan utføre L2-normalisering

L2-normalisering bruker L2-normen, som er kvadratroten av summen av de kvadrerte array-elementene.

Denne metoden konverterer den normaliserte matrisen til en enhetsvektor med en 2-norm på 1. L2-normalisering er nyttig for dimensjonsreduksjon og sikrer lik betydning for alle funksjoner.

Formelen for L2-normalisering er:

x' = x / sqrt(sum(x^2))

Slik kan du utføre L2-normalisering ved å bruke NumPy :

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform L2 normalization
l2_norm = np.linalg.norm(matrix, 2, axis=1, keepdims=True)
l2_normalized_matrix = matrix / l2_norm

print('Original Matrix:')
print(matrix)
print('nL2 Normalized Matrix:')
print(l2_normalized_matrix)

I denne koden beregner np.linalg.norm(matrise, 2, akse=1, keepdims=True) L2-normen (euklidsk norm) for hver rad (dette gjøres ved å spesifisere akse=1). Denne operasjonen vil returnere en kolonnevektor der hvert element er L2-normen til den tilsvarende raden.

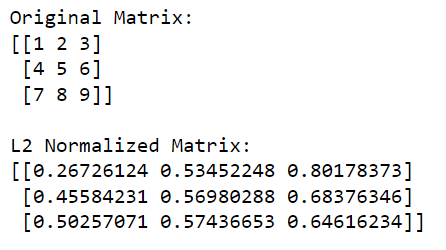
Ved å dele den opprinnelige matrisen med disse normene (utføre delingen element-vis), får vi den L2-normaliserte versjonen av matrisen.

Utgangen er gitt nedenfor:

Ok, nå som vi har gått gjennom de populære måtene å lage en normalisert matrise ved å bruke NumPy, la oss ta en titt på hvordan du kan gjøre det samme ved å bruke andre Python-biblioteker i neste seksjon.

Hvordan bruke Scikit-Learn for normalisering i Python

Scikit-learn er et kraftig Python-bibliotek for maskinlæring. Den gir flere verktøy for dataforbehandling.

Et verktøy du kan bruke er modulen sklearn.preprocessing , som tilbyr ulike teknikker for å utføre normalisering. Det er mange forskjellige skaleringsfunksjoner, transformatorer og normalisatorer tilgjengelig. Vi vil imidlertid fokusere på MinMaxScaler og normaliseringen .

For å forhåndsbehandle data med scikit-learn bruker du hovedsakelig transformator-API. Dette inkluderer metodene fit , transform og fit_transform .

1. Hvordan normalisere array ved hjelp av MinMaxScaler

MinMaxScaler er en skaler som normaliserer data til et spesifisert område , vanligvis [0, 1].

Formelen for MinMaxScalar er gitt nedenfor:

scaled_value = (value - min_value) / (max_value - min_value)

For å implementere MinMaxScaler kan du følge disse trinnene:

1. Importer de nødvendige bibliotekene:

   import numpy as np
   from sklearn.preprocessing import MinMaxScaler

2. Lag en NumPy-matrise:

   data = np.array([[1., 2., 5.], [3., 6., 8.], [5., 10., 12.]])

3. Instantier MinMaxScaler og tilpass den til dataene:

   scaler = MinMaxScaler()
   scaler.fit(data)

4. Transformer dataene ved å bruke transform- eller fit_transform -metoden:

   normalized_data = scaler.transform(data)

Utgangen av denne koden er gitt nedenfor:

Som du kan se i utdataene at MinMaxScalarMatrix bare har verdier fra 0 til 1.

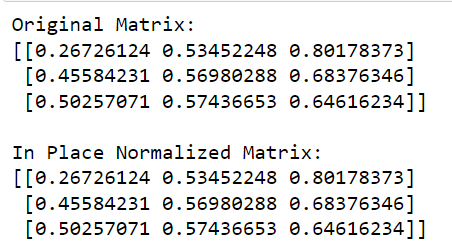
2. Hvordan utføre radnormalisering på stedet

Du kan også bruke på plass radnormalisering som et alternativ ved å bruke normaliseringsfunksjonen .

Denne metoden normaliserer hver inngangsmatrise eller funksjon uavhengig ved å skalere vektoren til en enhetsnorm. Som standard bruker normaliseringsfunksjonen L2-normen for å utføre enkel normalisering, men du kan velge andre normalternativer.

Følgende eksempel viser normalisering av rader på plass:

from sklearn.preprocessing import normalize
import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]], dtype=float)

# Apply in-place row normalization
normalize(matrix, norm='l2', copy=False)

print('L2 Normalized Matrix:')
print(matrix)

I denne koden kaller vi normaliseringsfunksjonen fra sklearn , definerer normen som skal brukes ('l2' i dette tilfellet), og setter copy=False for å utføre normalisering på stedet.

Utgangen av denne koden er gitt nedenfor:

For å lære mer om maskinlæring i , sjekk følgende video:

Siste tanker

Når du utforsker datavitenskap og maskinlæring ytterligere, vil du oppdage at normaliseringsprosessen er et viktig trinn i dataforbehandlingspipelinen din.

For det første plasserer den ulike funksjoner på en felles skala. Dette gjør modellene dine mindre følsomme for omfanget av innganger. Det kan i stor grad forbedre ytelsen til mange maskinlæringsalgoritmer.

For det andre hjelper det deg med å fremskynde treningsprosessen. Noen algoritmer, spesielt de som er basert på beregnede avstandsberegninger, konvergerer raskere når data er normalisert.

Ved å lære hvordan du normaliserer data, utstyrer du deg selv med en avgjørende ferdighet. Normalisering er et praktisk verktøy som brukes rutinemessig i virkelige applikasjoner. Det vil hjelpe deg med å redusere sannsynligheten for uventede resultater på grunn av uteliggere eller forskjeller i enheter.

Som ethvert verktøy ligger nøkkelen til å mestre normalisering i praksis. Så ikke nøl med å skitne hendene dine og eksperimentere med forskjellige datasett og tilfeldige verdier. Verden av er din østers. Lykke til med koding!