Til að hjálpa þér að skilja tölfræðilega greiningu með Excel, hjálpar það að líkja eftir Central Limit Theorem. Það hljómar næstum ekki rétt. Hvernig getur þýði sem er ekki normaldreifður valdið normaldreifðri sýnatökudreifingu?
Til að gefa þér hugmynd um hvernig Central Limit Theorem virkar er til eftirlíking. Þessi uppgerð skapar eitthvað eins og sýnatökudreifingu meðaltalsins fyrir mjög lítið úrtak, byggt á þýði sem er ekki venjulega dreift. Eins og þú munt sjá, jafnvel þó að þýðið sé ekki normaldreifing, og þó úrtakið sé lítið, lítur úrtaksdreifing meðaltalsins nokkuð út eins og normaldreifing.
Ímyndaðu þér risastórt þýði sem samanstendur af aðeins þremur stigum - 1, 2 og 3 - og hver og einn er jafn líklegur til að koma fram í úrtaki. Ímyndaðu þér líka að þú getur valið af handahófi úrtak af þremur stigum úr þessum þýði.
Öll möguleg sýni af þremur stigum (og aðferðum þeirra) úr þýði sem samanstendur af stigunum 1, 2 og 3
| Sýnishorn | Vondur | Sýnishorn | Vondur | Sýnishorn | Vondur |
| 1,1,1 | 1.00 | 2,1,1 | 1.33 | 3,1,1 | 1,67 |
| 1,1,2 | 1.33 | 2,1,2 | 1,67 | 3,1,2 | 2.00 |
| 1,1,3 | 1,67 | 2,1,3 | 2.00 | 3,1,3 | 2.33 |
| 1,2,1 | 1.33 | 2,2,1 | 1,67 | 3,2,1 | 2.00 |
| 1,2,2 | 1,67 | 2,2,2 | 2.00 | 3,2,2 | 2.33 |
| 1,2,3 | 2.00 | 2,2,3 | 2.33 | 3,2,3 | 2,67 |
| 1,3,1 | 1,67 | 2,3,1 | 2.00 | 3,3,1 | 2.33 |
| 1,3,2 | 2.00 | 2,3,2 | 2.33 | 3,3,2 | 2,67 |
| 1,3,3 | 2.33 | 2,3,3 | 2,67 | 3,3,3 | 3.00 |
Ef þú lítur vel á töfluna geturðu næstum séð hvað er að fara að gerast í uppgerðinni. Úrtaksmeðaltalið sem kemur oftast fram er 2,00. Úrtakið sem koma sjaldnast fram eru 1,00 og 3,00. Hmmm. . . .
Í uppgerðinni var stig valið af handahófi úr þýðinu og síðan valið af handahófi tvö til viðbótar. Sá hópur þriggja stiga er sýnishorn. Þá reiknarðu meðaltal þess úrtaks. Þetta ferli var endurtekið fyrir alls 60 sýni, sem leiddi til 60 sýnismiða. Að lokum teiknar þú dreifingu meðaltals úrtaks.
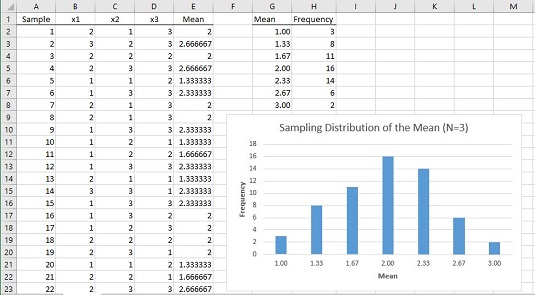
Hvernig lítur hermd sýnatökudreifing meðaltalsins út? Myndin hér að neðan sýnir vinnublað sem svarar þessari spurningu.
Í vinnublaðinu er hver röð sýnishorn. Dálkarnir merktir x1, x2 og x3 sýna þrjú stig fyrir hvert sýni. Dálkur E sýnir meðaltal úrtaksins í hverri röð. Dálkur G sýnir öll möguleg gildi fyrir meðaltal úrtaks og dálkur H sýnir hversu oft hvert meðaltal kemur fyrir í sýnunum 60. Dálkar G og H, og línuritið, sýna að dreifingin hefur hámarkstíðni þegar meðaltal úrtaks er 2,00. Tíðnirnar lækka eftir því sem sýnishornið fer lengra og lengra frá 2.00.
Aðalatriðið í þessu öllu er að þýðið lítur ekkert út eins og normaldreifing og úrtakið er mjög lítið. Jafnvel undir þeim takmörkunum fer sýnatökudreifing meðaltalsins miðað við 60 sýni að líkjast mjög eðlilegri dreifingu.
Hvað með færibreyturnar sem Miðmarkasetningin spáir fyrir um sýnatökudreifingu? Byrjaðu á íbúafjölda. Meðaltal íbúa er 2,00 og staðalfrávik íbúa er .67. (Þessi þýði krefst svolítið fínrar stærðfræði til að finna út færibreyturnar.)
Á dreifingu sýna. Meðaltal meðaltalanna 60 er 1,98 og staðalfrávik þeirra (mat á staðalfrávikum meðaltalsins) er 0,48. Þessar tölur ná nákvæmlega saman miðmörkum setningarinnar – spáð færibreytur fyrir sýnatökudreifingu meðaltalsins, 2,00 (jafnt þýðismeðaltali) og ,47 (staðalfrávikið, 0,67, deilt með kvaðratrótinni af 3, úrtaksstærð) .
Ef þú hefur áhuga á að gera þessa uppgerð, þá eru skrefin hér:
Veldu reit fyrir fyrsta númerið sem þú valdir af handahófi.
Veldu reit B2.
Notaðu vinnublaðsaðgerðina RANDBETWEEN til að velja 1, 2 eða 3.
Þetta líkir eftir því að teikna tölu úr þýði sem samanstendur af tölunum 1, 2 og 3 þar sem þú hefur jafna möguleika á að velja hverja tölu. Þú getur annað hvort valið FORMÚLUR | Stærðfræði og kveikja | RANDBETWEEN og notaðu Function Arguments valmyndina eða skrifaðu bara =RANDBETWEEN(1,3) í B2 og ýttu á Enter. Fyrsta röksemdin er minnsta talan RANDBETWEEN skilar, og önnur rökin eru stærsta talan.
Veldu reitinn hægra megin við upprunalega reitinn og veldu aðra slembitölu á milli 1 og 3. Gerðu þetta aftur fyrir þriðju slembitöluna í reitnum hægra megin við þann seinni.
Auðveldasta leiðin til að gera þetta er að fylla sjálfkrafa út í hólfin tvö hægra megin við upprunalega reitinn. Í þessu vinnublaði eru þessar tvær frumur C2 og D2.
Líttu á þessar þrjár frumur sem sýnishorn og reiknaðu meðaltal þeirra í frumunni hægra megin við þriðju frumuna.
Auðveldasta leiðin til að gera þetta er bara að slá inn =AVERAGE(B2:D2) í reit E2 og ýta á Enter.
Endurtaktu þetta ferli fyrir eins mörg sýni og þú vilt hafa með í uppgerðinni. Láttu hverja röð samsvara sýnishorni.
Hér voru notuð 60 sýni. Fljótlega og auðvelda leiðin til að gera þetta er að velja fyrstu línuna af þremur af handahófi völdum tölum og meðaltal þeirra og fylla síðan út þær línur sem eftir eru. Menngin af meðaltölum úrtaks í dálki E er hermd sýnatökudreifing meðaltalsins. Notaðu AVERAGE og STDEV.P til að finna meðaltal þess og staðalfrávik.
Til að sjá hvernig þessi herma sýnatökudreifing lítur út, notaðu fylkisaðgerðina FREQUENCY á sýnishorninu í dálki E. Fylgdu þessum skrefum:
Sláðu inn möguleg gildi meðaltals sýnisins í fylki.
Þú getur notað dálk G fyrir þetta. Þú getur tjáð möguleg gildi meðaltals úrtaksins í brotaformi (3/3, 4/3, 5/3, 6/3, 7/3, 8/3 og 9/3) eins og þau sem færð eru inn í frumurnar G2 til G8. Excel breytir þeim í aukastaf. Gakktu úr skugga um að þessar frumur séu á númerasniði.
Veldu fylki fyrir tíðni mögulegra gilda meðaltals úrtaks.
Þú getur notað dálk H til að halda tíðnunum, velja reiti H2 til H8.
Í valmyndinni Statistical Functions, veldu FREQUENCY til að opna Function Arguments valmyndina fyrir FREQUENCY
Í valmyndinni Function Arguments, sláðu inn viðeigandi gildi fyrir rökin.
Í Data_array reitnum, sláðu inn frumurnar sem geyma sýnishornið. Í þessu dæmi er það E2:E61.
Þekkja fylkið sem geymir möguleg gildi meðaltals úrtaksins.
FREQUENCY geymir þessa fylki í Bins_array kassanum. Fyrir þetta vinnublað fer G2:G8 í Bins_array reitinn. Eftir að þú hefur borið kennsl á báðar fylkin sýnir aðgerðarrök valmyndin tíðnirnar innan tveggja krullaðra sviga.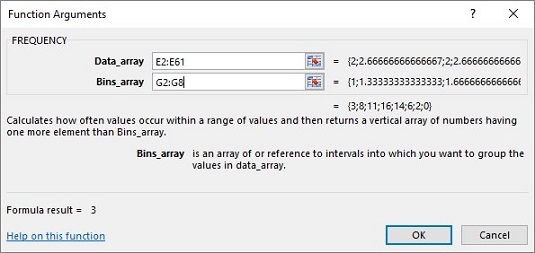
Ýttu á Ctrl+Shift+Enter til að loka glugganum Function Arguments og sýna tíðnirnar.
Notaðu þessa ásláttarsamsetningu vegna þess að FREQUENCY er fylkisaðgerð.
Að lokum, með H2:H8 auðkenndan, veldu Insert | Mælt er með myndritum og veldu Clustered Column skipulag til að búa til línuritið yfir tíðnirnar. Grafið þitt mun líklega líta nokkuð öðruvísi út en mitt, vegna þess að þú munt líklega lenda í annarri slembitölu.
Við the vegur, Excel endurtekur slembivalsferlið þegar þú gerir eitthvað sem veldur því að Excel endurreikur vinnublaðið. Áhrifin eru að tölurnar geta breyst þegar þú vinnur í gegnum þetta. (Þ.e.a.s. þú keyrir uppgerðina aftur.) Til dæmis, ef þú ferð til baka og fyllir út eina af línunum sjálfkrafa aftur, breytast tölurnar og grafið breytist.
Fyrir þá sem vilja læra um aðferðir eins og <strong>ROUND</strong>, <strong>ROUNDUP</strong> og <strong>ROUNDDOWN</strong> í Excel 2007, skoðaðu þessa skref-fyrir-skref leiðbeiningu um hvernig á að rúnna tölur á réttan hátt.
Hvernig á að koma í veg fyrir að Microsoft Word opni skrár í skrifvarandi ham á Windows. Microsoft Word opnar skrár í skrifvarandi ham, sem gerir það ómögulegt að breyta þeim? Ekki hafa áhyggjur, aðferðirnar eru hér að neðan
Hvernig á að laga villur við prentun á röngum Microsoft Word skjölum Villur við prentun Word skjala með breyttu letri, sóðalegar málsgreinar, texta sem vantar eða glatað efni eru nokkuð algengar. Hins vegar ekki
Ef þú hefur notað pennann eða hápunktarann til að teikna á PowerPoint glærurnar þínar meðan á kynningu stendur geturðu vistað teikningarnar fyrir næstu kynningu eða eytt þeim út svo næst þegar þú sýnir þær byrjarðu á hreinum PowerPoint glærum. Fylgdu þessum leiðbeiningum til að eyða penna- og auðkenningarteikningum: Að eyða línum einni á […]
Stílsafnið inniheldur CSS skrár, Extensible Stylesheet Language (XSL) skrár og myndir sem notaðar eru af fyrirfram skilgreindum aðalsíðum, síðuuppsetningum og stjórntækjum í SharePoint 2010. Til að finna CSS skrár í stílasafni útgáfusíðunnar: Veldu Site Actions→ View Allt efni á síðunni. Innihald síðunnar birtist. Style bókasafnið er staðsett í […]
Ekki yfirgnæfa áhorfendur með stórkostlegum tölum. Í Microsoft Excel geturðu bætt læsileika mælaborða og skýrslna með því að forsníða tölurnar þínar þannig að þær birtast í þúsundum eða milljónum.
Lærðu hvernig á að nota SharePoints samfélagsnetverkfæri sem gera einstaklingum og hópum kleift að eiga samskipti, vinna saman, deila og tengjast.
Julian dagsetningar eru oft notaðar í framleiðsluumhverfi sem tímastimpill og fljótleg tilvísun fyrir lotunúmer. Þessi tegund af dagsetningarkóðun gerir söluaðilum, neytendum og þjónustuaðilum kleift að bera kennsl á hvenær vara var framleidd og þar með aldur vörunnar. Julian dagsetningar eru einnig notaðar í forritun, hernum og stjörnufræði. Mismunandi […]
Þú getur búið til vefforrit í Access 2016. Svo hvað er vefforrit eiginlega? Jæja, vefurinn þýðir að hann er á netinu og app er bara stytting fyrir „umsókn“. Sérsniðið vefforrit er gagnagrunnsforrit á netinu sem hægt er að nálgast úr skýinu með vafra. Þú smíðar og viðheldur vefforritinu í skrifborðsútgáfunni […]
Flestar síður í SharePoint 2010 sýna lista yfir flakktengla á flýtiræsingarstikunni vinstra megin á síðunni. Flýtiræsingarstikan sýnir tengla á innihaldsefni vefsvæða eins og lista, bókasöfn, síður og útgáfusíður. Flýtiræsingarstikan inniheldur tvo mjög mikilvæga tengla: Tengill á allt efni vefsvæðis: […]
