Poisson getur verið mjög gagnlegt tæki þegar nálgast tölfræðilega greiningu með Excel. Ekki sýna hvernig það virkar? Hér eru skrefin til að nota Excel's POISSON.DIST:
Veldu reit fyrir svar POISSON.DIST.
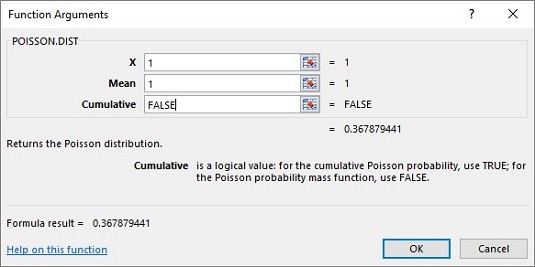
Í Statistical Functions valmyndinni, veldu POISSON.DIST til að opna Function Arguments valmyndina.
Í valmyndinni Function Arguments, sláðu inn viðeigandi gildi fyrir rökin.
Í X reitnum skaltu slá inn fjölda atburða sem þú ert að ákvarða líkurnar á. Fyrir þetta dæmi ertu að leita að pr (1), svo sláðu inn 1.
Í Meðaltalsreitnum skaltu slá inn meðaltal ferlisins, sem fyrir þetta dæmi er 1.
Í Uppsafnaðar kassanum er það annað hvort TRUE fyrir uppsafnaðar líkur eða FALSE fyrir bara líkurnar á fjölda atburða. Sláðu inn FALSE.
Með færslunum fyrir X, Meðaltal og Uppsafnað birtist svarið í svarglugganum. Svarið fyrir þetta dæmi er .367879441.
Smelltu á Í lagi til að setja svarið í valinn reit.
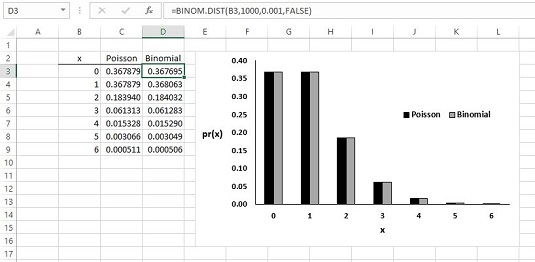
Í dæminu sérðu líkurnar á tveimur gölluðum liðum í 1.000 og líkurnar á þremur. Til að fylgja útreikningunum eftir skaltu slá inn 2 í X reitinn til að reikna pr (2) og 3 til að finna pr (3).
Á 21. öldinni er frekar auðvelt að reikna út tvíliðalíkurnar beint. Myndin hér að neðan sýnir þér Poisson- og tvínefnalíkur fyrir tölurnar í dálki B og skilyrði dæmisins. Líkurnar eru teknar upp á línuriti svo þú getir séð hversu nálægir tveir eru í raun. Hólf D3 var valið, þannig að formúlastúlan sýnir þér hvernig BINOM.DIST var notað til að reikna út tvíliðalíkurnar.
Þó að notagildi Poisson sem nálgun sé úrelt hefur hann öðlast sitt eigið líf. Fyrirbæri sem eru jafn misjöfn og gögn um viðbragðstíma í sálfræðitilraunum, hrörnun geislavirkra efna og stig í atvinnuhokkíleikjum virðast passa við Poisson dreifingu. Þetta er ástæðan fyrir því að viðskiptafræðingar og vísindamenn vilja byggja líkan á þessari dreifingu.
Fyrir þá sem vilja læra um aðferðir eins og <strong>ROUND</strong>, <strong>ROUNDUP</strong> og <strong>ROUNDDOWN</strong> í Excel 2007, skoðaðu þessa skref-fyrir-skref leiðbeiningu um hvernig á að rúnna tölur á réttan hátt.
Hvernig á að koma í veg fyrir að Microsoft Word opni skrár í skrifvarandi ham á Windows. Microsoft Word opnar skrár í skrifvarandi ham, sem gerir það ómögulegt að breyta þeim? Ekki hafa áhyggjur, aðferðirnar eru hér að neðan
Hvernig á að laga villur við prentun á röngum Microsoft Word skjölum Villur við prentun Word skjala með breyttu letri, sóðalegar málsgreinar, texta sem vantar eða glatað efni eru nokkuð algengar. Hins vegar ekki
Ef þú hefur notað pennann eða hápunktarann til að teikna á PowerPoint glærurnar þínar meðan á kynningu stendur geturðu vistað teikningarnar fyrir næstu kynningu eða eytt þeim út svo næst þegar þú sýnir þær byrjarðu á hreinum PowerPoint glærum. Fylgdu þessum leiðbeiningum til að eyða penna- og auðkenningarteikningum: Að eyða línum einni á […]
Stílsafnið inniheldur CSS skrár, Extensible Stylesheet Language (XSL) skrár og myndir sem notaðar eru af fyrirfram skilgreindum aðalsíðum, síðuuppsetningum og stjórntækjum í SharePoint 2010. Til að finna CSS skrár í stílasafni útgáfusíðunnar: Veldu Site Actions→ View Allt efni á síðunni. Innihald síðunnar birtist. Style bókasafnið er staðsett í […]
Ekki yfirgnæfa áhorfendur með stórkostlegum tölum. Í Microsoft Excel geturðu bætt læsileika mælaborða og skýrslna með því að forsníða tölurnar þínar þannig að þær birtast í þúsundum eða milljónum.
Lærðu hvernig á að nota SharePoints samfélagsnetverkfæri sem gera einstaklingum og hópum kleift að eiga samskipti, vinna saman, deila og tengjast.
Julian dagsetningar eru oft notaðar í framleiðsluumhverfi sem tímastimpill og fljótleg tilvísun fyrir lotunúmer. Þessi tegund af dagsetningarkóðun gerir söluaðilum, neytendum og þjónustuaðilum kleift að bera kennsl á hvenær vara var framleidd og þar með aldur vörunnar. Julian dagsetningar eru einnig notaðar í forritun, hernum og stjörnufræði. Mismunandi […]
Þú getur búið til vefforrit í Access 2016. Svo hvað er vefforrit eiginlega? Jæja, vefurinn þýðir að hann er á netinu og app er bara stytting fyrir „umsókn“. Sérsniðið vefforrit er gagnagrunnsforrit á netinu sem hægt er að nálgast úr skýinu með vafra. Þú smíðar og viðheldur vefforritinu í skrifborðsútgáfunni […]
Flestar síður í SharePoint 2010 sýna lista yfir flakktengla á flýtiræsingarstikunni vinstra megin á síðunni. Flýtiræsingarstikan sýnir tengla á innihaldsefni vefsvæða eins og lista, bókasöfn, síður og útgáfusíður. Flýtiræsingarstikan inniheldur tvo mjög mikilvæga tengla: Tengill á allt efni vefsvæðis: […]
