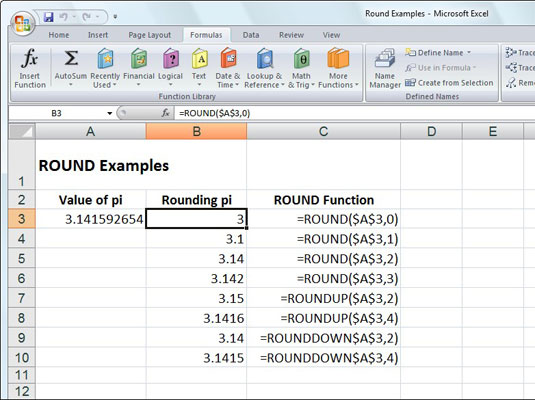
Excel er frábært tól þegar þú þarft að nota tölfræði. Ef þú hefur aldrei kynnst tölfræði í skóla eða það er áratugur eða tveir síðan þú varst, láttu þessar ráðleggingar hjálpa þér að nota nokkur af tölfræðiverkfærunum sem Excel býður upp á.
Það fyrsta sem þú ættir að vita er að einhver tölfræðileg greining og sumar tölfræðilegar mælingar eru frekar einfalt. Lýsandi tölfræði, sem felur í sér hluti eins og snúningstöflu krosstöflur, auk sumra tölfræðilegra aðgerða, er skynsamleg jafnvel fyrir einhvern sem er ekki svo magnbundinn.
Þegar einhver notar hugtakið meðaltal, er það sem hann vísar venjulega til algengasta meðaltalsmælingarinnar, sem er meðaltal. Skilningur á því að hugtakið meðaltal er ónákvæmt gerir mikið af tölfræðilegri virkni Excel skiljanlegra.
Til að gera þessa umræðu áþreifanlegri skaltu gera ráð fyrir að þú sért að horfa á lítið safn af gildum: 1, 2, 3, 4 og 5. Eins og þú kannski veist er meðaltalið í þessu litla gildismati 3. Þú getur reiknað út meðaltalið með því að leggja saman allar tölurnar í menginu (1+2+3+4+5) og deila síðan þessari summu (15) með heildarfjölda gilda í menginu (5).
The miðgildi er gildi sem skilur stærstu gildin frá minnstu gildi. Í gagnasafninu 1, 2, 3, 4 og 5 er miðgildið 3. Gildið 3 skilur stærstu gildin (4 og 5) frá minnstu gildunum (1 og 2).
Þú þarft ekki að skilja mismunandi meðaltalsmælingar, en þú ættir að muna að hugtakið meðaltal er frekar ónákvæmt.
Formúlan fyrir staðalfrávik og rökfræðin er frekar auðvelt að skilja.
A staðalfrávik er því lýst hvernig gildin í gagnasafns verið í kringum meðaltal. Það sniðuga við tölfræðilegar mælingar eins og staðalfrávik, þú færð oft raunverulega innsýn í eiginleika gagna sem þú ert að skoða. Annað er að með þessum tveimur gagnabitum er oft hægt að draga ályktanir um gögn með því að skoða sýnishorn.
Athugun er eitt af hugtökum sem þú munt lenda í ef þú lest eitthvað um tölfræði. Athugun er bara athugun. Ein leið til að skilgreina hugtakið athugun er svona: Alltaf þegar þú gefur í raun gildi einni af handahófskenndu breytunum þínum býrðu til athugun.
A sýni er safn af athugasemdum frá íbúum. Til dæmis, ef þú býrð til gagnasett sem skráir daglegan háan hita í hverfinu þínu, er litla safnið þitt af athugunum sýnishorn.
Til samanburðar er úrtak ekki þýði. A íbúa nær allar mögulegar athugasemdir.
Ef þú skoðar úrtak af gildum úr þýði og úrtakið er dæmigert og nógu stórt, getur þú dregið ályktanir um þýðið út frá eiginleikum úrtaksins.
Ályktunartölfræði, þó hún sé mjög öflug, hefur tvo eiginleika sem þú þarft að vita:
Nákvæmni vandamál
Brattur námsferill
P robability dreifingu virka hljómar nokkuð erfiður; en þú getur í raun skilið innsæi hvað líkindadreifingaraðgerð er með nokkrum gagnlegum dæmum.
Ein algeng dreifing sem þú heyrir um í tölfræðitímum, til dæmis, er T dreifing. A T dreifing er í meginatriðum a normaldreifing, nema með þyngri, feitari hala.
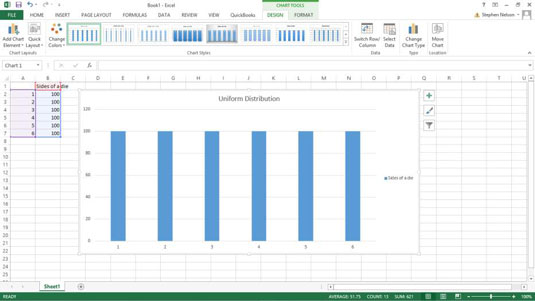
Eitt algengt líkindadreifingarfall er samræmd dreifing. Í samræmdri dreifingu hafa allir atburðir sömu líkur á að hann gerist. Það einstaka við þessa dreifingu er að allt er frekar bölvað.
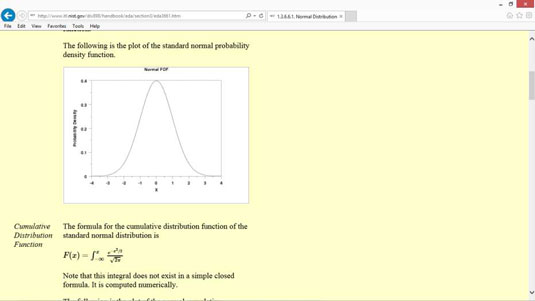
Önnur algeng tegund líkindadreifingarfalls er normaldreifing, einnig þekkt sem bjöllukúrfa eða Gaussdreifing.
Eðlileg dreifing á sér stað náttúrulega í mörgum aðstæðum. Til dæmis dreifast greindarhlutföll (IQs) eðlilega.
A breytu er inntak til Líkindadreifingarfall. Með öðrum orðum, formúlan eða fallið eða jöfnan sem lýsir líkindadreifingarferli þarf inntak. Í tölfræði eru þessi inntak kölluð færibreytur.
Sumar líkindadreifingaraðgerðir þurfa aðeins eina einfalda færibreytu. Til dæmis, til að vinna með samræmda dreifingu, er allt sem þú þarft í raun og veru fjöldi gilda í gagnasafninu. Sexhliða teningur, til dæmis, hefur aðeins sex möguleika.
Nokkur önnur gagnleg tölfræðileg hugtök sem þú þarft að vita eru skewness og kurtosis. Skekkja mælir skort á samhverfu í líkindadreifingu. Í fullkomlega samhverfri dreifingu, eins og normaldreifingu, er skekkjan núll. Ef líkindadreifing hallast hins vegar til hægri eða vinstri jafngildir skekkjan einhverju öðru gildi en núlli og gildið mælir skort á samhverfu.
Kurtosis mælir þyngd hala í dreifingu. Í normaldreifingu er kurtosis núll. The hali er hlutur sem nær út til vinstri eða hægri. Hins vegar, ef hali í dreifingu er þyngri en normaldreifing, er kurtosis jákvæð tala. Ef halar í dreifingu eru horaðar en í normaldreifingu er kurtósa neikvæð tala.
Líkurnar rugla oft fólk. Mikilvægt að skilja varðandi öryggisstig er að þau eru tengd við skekkjumörk.
Annar mikilvægur hlutur til að skilja varðandi öryggisstig er að því stærri sem þú gerir úrtaksstærð þína, því minni skekkjumörk mun nota sama öryggisstig.
Sem aðeins eitt dæmi, segðu að þú hafir haft nokkur Google Analytics gögn um tvær mismunandi vefauglýsingar sem þú ert að birta til að kynna lítið fyrirtæki þitt og þú vilt vita hvaða auglýsing er skilvirkari. Þú getur notað öryggisbilsformúluna til að reikna út hversu lengi auglýsingarnar þínar þurfa að birtast áður en Google safnar nægum gögnum til að þú veist hvaða auglýsing er raunverulega betri.
Fyrir þá sem vilja læra um aðferðir eins og <strong>ROUND</strong>, <strong>ROUNDUP</strong> og <strong>ROUNDDOWN</strong> í Excel 2007, skoðaðu þessa skref-fyrir-skref leiðbeiningu um hvernig á að rúnna tölur á réttan hátt.
Hvernig á að koma í veg fyrir að Microsoft Word opni skrár í skrifvarandi ham á Windows. Microsoft Word opnar skrár í skrifvarandi ham, sem gerir það ómögulegt að breyta þeim? Ekki hafa áhyggjur, aðferðirnar eru hér að neðan
Hvernig á að laga villur við prentun á röngum Microsoft Word skjölum Villur við prentun Word skjala með breyttu letri, sóðalegar málsgreinar, texta sem vantar eða glatað efni eru nokkuð algengar. Hins vegar ekki
Ef þú hefur notað pennann eða hápunktarann til að teikna á PowerPoint glærurnar þínar meðan á kynningu stendur geturðu vistað teikningarnar fyrir næstu kynningu eða eytt þeim út svo næst þegar þú sýnir þær byrjarðu á hreinum PowerPoint glærum. Fylgdu þessum leiðbeiningum til að eyða penna- og auðkenningarteikningum: Að eyða línum einni á […]
Stílsafnið inniheldur CSS skrár, Extensible Stylesheet Language (XSL) skrár og myndir sem notaðar eru af fyrirfram skilgreindum aðalsíðum, síðuuppsetningum og stjórntækjum í SharePoint 2010. Til að finna CSS skrár í stílasafni útgáfusíðunnar: Veldu Site Actions→ View Allt efni á síðunni. Innihald síðunnar birtist. Style bókasafnið er staðsett í […]
Ekki yfirgnæfa áhorfendur með stórkostlegum tölum. Í Microsoft Excel geturðu bætt læsileika mælaborða og skýrslna með því að forsníða tölurnar þínar þannig að þær birtast í þúsundum eða milljónum.
Lærðu hvernig á að nota SharePoints samfélagsnetverkfæri sem gera einstaklingum og hópum kleift að eiga samskipti, vinna saman, deila og tengjast.
Julian dagsetningar eru oft notaðar í framleiðsluumhverfi sem tímastimpill og fljótleg tilvísun fyrir lotunúmer. Þessi tegund af dagsetningarkóðun gerir söluaðilum, neytendum og þjónustuaðilum kleift að bera kennsl á hvenær vara var framleidd og þar með aldur vörunnar. Julian dagsetningar eru einnig notaðar í forritun, hernum og stjörnufræði. Mismunandi […]
Þú getur búið til vefforrit í Access 2016. Svo hvað er vefforrit eiginlega? Jæja, vefurinn þýðir að hann er á netinu og app er bara stytting fyrir „umsókn“. Sérsniðið vefforrit er gagnagrunnsforrit á netinu sem hægt er að nálgast úr skýinu með vafra. Þú smíðar og viðheldur vefforritinu í skrifborðsútgáfunni […]
Flestar síður í SharePoint 2010 sýna lista yfir flakktengla á flýtiræsingarstikunni vinstra megin á síðunni. Flýtiræsingarstikan sýnir tengla á innihaldsefni vefsvæða eins og lista, bókasöfn, síður og útgáfusíður. Flýtiræsingarstikan inniheldur tvo mjög mikilvæga tengla: Tengill á allt efni vefsvæðis: […]
