NumPy-taulukoiden normalisointi: Pikaopas

Jos olet työskennellyt Pythonin kanssa tietojen analysoinnissa tai koneoppimisessa, olet todennäköisesti törmännyt NumPy-taulukoihin. Ne ovat tehokas työkalu numeeristen tietojen käsittelyyn, mutta joskus näiden taulukoiden tietoja on säädettävä tai "normalisoitava", jotta niitä voidaan käyttää tehokkaasti algoritmeissasi. Mutta mitä taulukon normalisointi tarkoittaa?

NumPy-taulukon normalisoimiseksi sinun on säädettävä taulukon arvot niin, että ne ovat tietyllä alueella, tyypillisesti välillä 0 ja 1, tai niin, että niillä on normaali normaalijakauma, jonka keskiarvo on 0 ja keskihajonta 1. Tämä tehdään usein koneoppimisen ja data-analyysin alalla sen varmistamiseksi, että kaikilla syöttöominaisuuksilla on sama mittakaava.

Tässä artikkelissa tutkimme, kuinka voit normalisoida NumPy-taulukon Pythonissa. Tarkastellaan erilaisia ​​menetelmiä, joilla voit normalisoida NumPy-taulukon, ja tarkastellaan myös esimerkkejä, jotka auttavat sinua ymmärtämään käsitteen paremmin.

Mennään asiaan!

Sisällysluettelo

• Mitkä ovat Pythonin normalisoinnin perusteet?
  • Mitä on normalisointi?
  • Miksi normalisointi on tärkeää?
  • Mitä ovat normit?
  • Mitä on normalisointi koneoppimisessa?
• Mitkä ovat Pythonin normalisointitekniikat?
  • 1. Min-Max-skaalaus
  • 2. L1-normalisoinnin suorittaminen
  • 3. L2-normalisoinnin suorittaminen
• Scikit-Learnin käyttäminen normalisointiin Pythonissa
  • 1. Array normalisointi MinMaxScalerilla
  • 2. Paikalla tapahtuvan rivin normalisoinnin suorittaminen
• Lopulliset ajatukset

Mitkä ovat Pythonin normalisoinnin perusteet?

Ennen kuin otamme normalisoinnin käyttöön Pythonissa, sinun on ymmärrettävä, mitä normalisointi tarkoittaa.

Siksi tässä osiossa käymme läpi, mikä on normalisointi ja sen ydinkäsitteet.

Mitä on normalisointi?

Normalisointi on prosessi, joka skaalaa ja muuntaa tiedot standardoiduksi alueeksi. Tämä tehdään jakamalla jokainen datan elementti parametrilla . Parametri voi olla maksimiarvo, alue tai jokin muu normi.

Voit normalisoida NumPy-taulukon käyttämällä euklidista normia (tunnetaan myös L2-normina). Lisäksi voit myös normalisoida NumPy-taulukoita skaalaamalla arvot tietyn alueen välillä, yleensä 0 - 1.

Pythonissa NumPy-kirjasto tarjoaa tehokkaan tavan normalisoida taulukoita. Tämä sisältää myös moniulotteiset taulukot ja matriisit.

Miksi normalisointi on tärkeää?

Normalisointi on tärkeää, sillä sen avulla varmistetaan, että eri ominaisuuksia käsitellään tasavertaisesti vertailtaessa ja analysoitaessa tietoja. Voit käyttää sitä eliminoimaan mahdollisia harhoja tai poikkeavuuksia, joita saattaa syntyä vaihtelevista mittasuhteista johtuen.

Mitä ovat normit?

Normalisointiin käyttämäsi parametri voi olla eri normeja , kuten Euklidinen normi (L2), Manhattanin normi (L1) tai maksiminormi (L_inf). Käytät normeja laskeaksesi vektorin tai matriisin suuruuden . Näitä käytetään sitten skaalaustekijänä tietojen normalisoimiseksi.

Matriisien kanssa työskennellessämme käytämme usein Frobenius-normia , joka on yleistys euklidisesta normista moniulotteisille taulukoille.

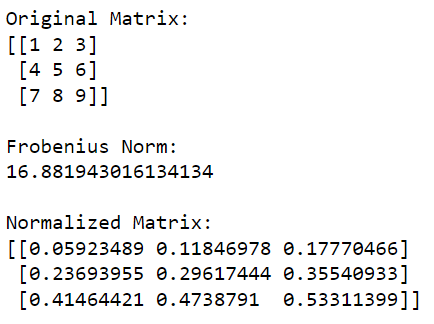
Seuraava esimerkki näyttää matriisin normalisoinnin Frobenius-normin avulla:

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Calculate the Frobenius norm
frobenius_norm = np.linalg.norm(matrix, 'fro')

# Normalize the matrix
normalized_matrix = matrix / frobenius_norm

print('Original Matrix:')
print(matrix)
print('nFrobenius Norm:')
print(frobenius_norm)
print('nNormalized Matrix:')
print(normalized_matrix)

Tämä Python-koodi tuo ensin NumPy-kirjaston ja käyttää sitä matriisin luomiseen. Sitten se laskee matriisin Frobenius-normin ja jakaa sitten jokaisen matriisin elementin tällä arvolla normalisoidakseen sen.

Tämän koodin tulos on annettu alla:

Mitä on normalisointi koneoppimisessa?

Koneoppimisessa normalisointi on tärkeä esikäsittelyvaihe , koska se parantaa algoritmien suorituskykyä.

Kun suoritat gradienttipohjaisia ​​optimointitekniikoita, huomaat, että optimoidut ominaisuudet pyrkivät lähentymään nopeammin ja tehokkaammin. Tämä johtuu siitä, että se vähentää huonon skaalauksen tai katoavien gradienttien riskiä.

Mitkä ovat Pythonin normalisointitekniikat?

Voit suorittaa taulukoiden normalisoinnin useilla tavoilla. Jotkut menetelmät ovat kuitenkin suositumpia kuin toiset korkean tehokkuutensa vuoksi.

Tässä osiossa tarkastellaan kolmea yleisesti käytettyä normalisointitekniikkaa:

1. Min-Max Skaalaus

2. L1 Normalisointi

3. L2 Normalisointi

1. Min-Max-skaalaus

Min-max-skaalaus tunnetaan myös lineaarisena normalisoinna tai ominaisuuden skaalauksena. Min-max-skaalauksessa skaalaamme NumPy-taulukon arvot siten, että ne ovat tietyllä alueella, tyypillisesti välillä 0 ja 1.

Tätä varten vähennät vähimmäisarvon kustakin elementistä ja jaat tuloksen enimmäis- ja vähimmäisarvon erolla.

Voit esittää min-max-skaalauksen matemaattisesti seuraavasti:

x' = (x - min(x)) / (max(x) - min(x))

Seuraava esimerkki havainnollistaa, kuinka voit suorittaa min-max-skaalauksen NumPy-kirjaston avulla:

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform min-max scaling
min_val = np.min(matrix)
max_val = np.max(matrix)

scaled_matrix = (matrix - min_val) / (max_val - min_val)

print('Original Matrix:')
print(matrix)
print('nMin-Max Scaled Matrix:')
print(scaled_matrix)

Tämä koodi tuo ensin NumPy:n ja laskee sitten matriisin minimi- ja maksimiarvot, jotka sitten skaalataan siten, että kaikki arvot ovat välillä 0 (vastaa alkuperäistä minimiarvoa) ja 1 (vastaa alkuperäistä maksimiarvoa).

Tämän koodin tulos on annettu alla:

Min-max-skaalaus on erittäin yleinen skaalausmuoto koneoppimisessa ja tietojen esikäsittelyssä.

2. L1-normalisoinnin suorittaminen

L1-normalisoinnissa käytetään L1-normia, joka on taulukon elementtien itseisarvojen summa. Tämä on erityisen hyödyllistä harvoille matriiseille. Se varmistaa, että normalisoitujen taulukon elementtien absoluuttisten arvojen summa on yhtä suuri kuin 1.

L1-normalisoinnin kaava on:

x' = x / sum(|x|)

Seuraava esimerkki näyttää, kuinka voit suorittaa L1-normalisoinnin NumPy:n avulla:

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform L1 normalization
l1_norm = np.linalg.norm(matrix, 1, axis=1, keepdims=True)
l1_normalized_matrix = matrix / l1_norm

print('Original Matrix:')
print(matrix)
print('nL1 Normalized Matrix:')
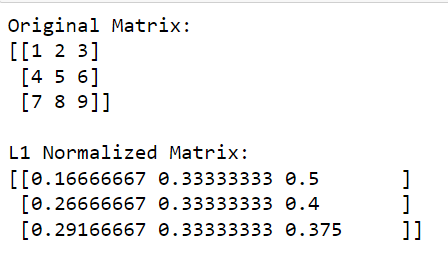
print(l1_normalized_matrix)

Tässä koodissa np.linalg.norm (matriisi, 1, akseli=1, keepdims=True) laskee L1-normin jokaiselle riville (tämä tehdään määrittämällä akseli=1).

Tämä toiminto palauttaa sarakevektorin, jossa jokainen elementti on vastaavan rivin L1-normi. Jakamalla alkuperäinen matriisi näillä normeilla (suorittamalla jakoelementtien mukaan) saadaan matriisin L1 normalisoitu versio.

Tulos on alla:

3. L2-normalisoinnin suorittaminen

L2-normalisointi käyttää L2-normia, joka on neliöjuuri taulukon neliöelementtien summasta.

Tämä menetelmä muuntaa normalisoidun taulukon yksikkövektoriksi, jonka 2-normi on 1. L2-normalisointi on hyödyllinen dimensioiden pienentämisessä ja varmistaa yhtäläisen merkityksen kaikille piirteille.

L2-normalisoinnin kaava on:

x' = x / sqrt(sum(x^2))

Näin voit suorittaa L2-normalisoinnin NumPy:n avulla :

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform L2 normalization
l2_norm = np.linalg.norm(matrix, 2, axis=1, keepdims=True)
l2_normalized_matrix = matrix / l2_norm

print('Original Matrix:')
print(matrix)
print('nL2 Normalized Matrix:')
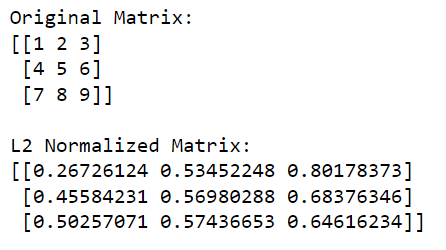
print(l2_normalized_matrix)

Tässä koodissa np.linalg.norm(matriisi, 2, akseli=1, keepdims=True) laskee L2-normin (euklidisen normin) jokaiselle riville (tämä tehdään määrittämällä akseli=1). Tämä toiminto palauttaa sarakevektorin, jossa jokainen elementti on vastaavan rivin L2-normi.

Jakamalla alkuperäinen matriisi näillä normeilla (suorittamalla jakoelementtien mukaan) saadaan matriisin L2-normalisoitu versio.

Tulos on alla:

Selvä, nyt kun olemme käyneet läpi suosittuja tapoja luoda normalisoitu taulukko NumPyllä, katsotaanpa seuraavassa osiossa, kuinka voit tehdä saman käyttämällä muita Python-kirjastoja.

Scikit-Learnin käyttäminen normalisointiin Pythonissa

Scikit-learn on tehokas Python-kirjasto koneoppimiseen. Se tarjoaa useita työkaluja tietojen esikäsittelyyn.

Yksi työkalu, jota voit käyttää, on sklearn.preprocessing -moduuli, joka tarjoaa erilaisia ​​tekniikoita normalisoinnin suorittamiseen. Saatavilla on monia erilaisia ​​skaalaustoimintoja, muuntajia ja normalisoijia. Keskitymme kuitenkin MinMaxScaleriin ja normalisointiin .

Tietojen esikäsittelyyn scikit-learnillä käytetään pääasiassa muuntajan API:ta. Tämä sisältää menetelmät sovitus , muunnos ja sovi_muunnos .

1. Array normalisointi MinMaxScalerilla

MinMaxScaler on skaalaus, joka normalisoi tiedot tietylle alueelle, yleensä [0, 1] .

MinMaxScalarin kaava on annettu alla:

scaled_value = (value - min_value) / (max_value - min_value)

Voit ottaa MinMaxScaler käyttöön seuraavasti:

1. Tuo tarvittavat kirjastot:

   import numpy as np
   from sklearn.preprocessing import MinMaxScaler

2. Luo NumPy-taulukko:

   data = np.array([[1., 2., 5.], [3., 6., 8.], [5., 10., 12.]])

3. Instantoi MinMaxScaler ja sovita se tietoihin:

   scaler = MinMaxScaler()
   scaler.fit(data)

4. Muunna tiedot muunnos- tai fit_transform - menetelmällä:

   normalized_data = scaler.transform(data)

Tämän koodin tulos on annettu alla:

Kuten voit nähdä lähdöstä, että MinMaxScalarMatrixin arvot vaihtelevat vain välillä 0 - 1.

2. Paikalla tapahtuvan rivin normalisoinnin suorittaminen

Vaihtoehtona voit käyttää myös rivin paikallista normalisointia käyttämällä normalisointitoimintoa .

Tämä menetelmä normalisoi jokaisen syötetaulukon tai ominaisuuden itsenäisesti skaalaamalla vektorin yksikkönormiin. Normalisointitoiminto käyttää oletusarvoisesti L2-normia yksinkertaisen normalisoinnin suorittamiseen, mutta voit valita muita normivaihtoehtoja.

Seuraava esimerkki osoittaa rivien normalisoinnin:

from sklearn.preprocessing import normalize
import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]], dtype=float)

# Apply in-place row normalization
normalize(matrix, norm='l2', copy=False)

print('L2 Normalized Matrix:')
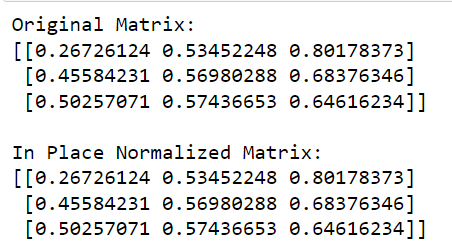
print(matrix)

Tässä koodissa kutsumme normalisointifunktiota sklearnistä , määritämme käytettävän normin (tässä tapauksessa 'l2') ja asetamme copy=False suorittamaan paikallisen normalisoinnin.

Tämän koodin tulos on annettu alla:

Jos haluat lisätietoja koneoppimisesta kohteessa , katso seuraava video:

Lopulliset ajatukset

Kun tutkit edelleen datatieteitä ja koneoppimista, huomaat, että normalisointiprosessi on olennainen vaihe tietojen esikäsittelyssäsi.

Ensinnäkin se asettaa erilaiset ominaisuudet yhteiselle mittakaavalle. Tämä tekee malleistasi vähemmän herkkiä tulojen asteikolle. Se voi parantaa huomattavasti monien koneoppimisalgoritmien suorituskykyä.

Toiseksi se auttaa sinua nopeuttamaan harjoitusprosessia. Jotkut algoritmit, erityisesti ne, jotka perustuvat laskettuun etäisyyslaskelmaan, konvergoivat nopeammin, kun tiedot normalisoidaan.

Oppimalla normalisoimaan dataa saat tärkeän taidon. Normalisointi on käytännöllinen työkalu, jota käytetään rutiininomaisesti tosielämän sovelluksissa. Se auttaa sinua vähentämään odottamattomien tulosten todennäköisyyttä poikkeavuuksista tai yksiköiden eroista.

Kuten kaikki työkalut, avain normalisoinnin hallitsemiseen on käytännössä. Älä siis epäröi likaantua ja kokeilla erilaisia ​​tietojoukkoja ja satunnaisia ​​arvoja. Maailma on sinun osterisi. Hyvää koodausta!