Πώς να προσκαλέσετε άτομα στον διακομιστή Discord σας
Μάθετε πώς να στέλνετε προσκλήσεις στον διακομιστή Discord σας και πώς να αναπτύξετε την διαδικτυακή σας κοινότητα.
Το θεώρημα του Bayes μπορεί να σας βοηθήσει να συμπεράνετε πόσο πιθανό είναι να συμβεί κάτι σε ένα συγκεκριμένο πλαίσιο, με βάση τις γενικές πιθανότητες του ίδιου του γεγονότος και των αποδεικτικών στοιχείων που εξετάζετε, και σε συνδυασμό με την πιθανότητα των αποδεικτικών στοιχείων δεδομένου του γεγονότος. Σπάνια ένα μόνο αποδεικτικό στοιχείο θα μειώσει τις αμφιβολίες και θα παρέχει αρκετή βεβαιότητα σε μια πρόβλεψη ώστε να διασφαλιστεί ότι θα συμβεί. Ως αληθινός ντετέκτιβ, για να φτάσετε στη βεβαιότητα, πρέπει να συλλέξετε περισσότερα στοιχεία και να κάνετε τα μεμονωμένα κομμάτια να συνεργαστούν στην έρευνά σας. Η παρατήρηση ότι ένα άτομο έχει μακριά μαλλιά δεν αρκεί για να καθορίσει εάν το άτομο είναι θηλυκό ή αρσενικό. Η προσθήκη δεδομένων σχετικά με το ύψος και το βάρος θα μπορούσε να βοηθήσει στην αύξηση της αυτοπεποίθησης.
Ο αλγόριθμος Naïve Bayes σάς βοηθά να οργανώσετε όλα τα στοιχεία που συγκεντρώνετε και να φτάσετε σε μια πιο στέρεη πρόβλεψη με μεγαλύτερη πιθανότητα να είναι σωστή. Τα συγκεντρωμένα στοιχεία που θεωρούνται μοναδικά δεν θα μπορούσαν να σας γλιτώσουν από τον κίνδυνο εσφαλμένης πρόβλεψης, αλλά όλα τα στοιχεία που αθροίζονται μαζί μπορούν να φτάσουν σε μια πιο οριστική επίλυση. Το ακόλουθο παράδειγμα δείχνει πώς λειτουργούν τα πράγματα σε μια ταξινόμηση Naïve Bayes. Αυτό είναι ένα παλιό, διάσημο πρόβλημα, αλλά αντιπροσωπεύει το είδος της ικανότητας που μπορείτε να περιμένετε από ένα AI. Το σύνολο δεδομένων προέρχεται από την εργασία « Induction of Decision Trees», του John Ross Quinlan. Ο Quinlan είναι ένας επιστήμονας υπολογιστών που συνέβαλε στην ανάπτυξη ενός άλλου αλγορίθμου μηχανικής μάθησης, των δέντρων αποφάσεων, με θεμελιώδη τρόπο, αλλά το παράδειγμά του λειτουργεί καλά με κάθε είδους αλγόριθμο μάθησης. Το πρόβλημα απαιτεί από το AI να μαντέψει τις καλύτερες συνθήκες για να παίξεις τένις δεδομένων των καιρικών συνθηκών. Το σύνολο των χαρακτηριστικών που περιγράφονται από τον Quinlan είναι το εξής:
Ο παρακάτω πίνακας περιέχει τις εγγραφές της βάσης δεδομένων που χρησιμοποιούνται για το παράδειγμα:
| Αποψη | Θερμοκρασία | Υγρασία | Ανεμώδης | Παίξε αντισφαίριση |
| Ηλιόλουστος | Ζεστό | Υψηλός | Ψευδής | Οχι |
| Ηλιόλουστος | Ζεστό | Υψηλός | Αληθής | Οχι |
| Νεφελώδης | Ζεστό | Υψηλός | Ψευδής | Ναί |
| Βροχερός | Ήπιος | Υψηλός | Ψευδής | Ναί |
| Βροχερός | Δροσερός | Κανονικός | Ψευδής | Ναί |
| Βροχερός | Δροσερός | Κανονικός | Αληθής | Οχι |
| Νεφελώδης | Δροσερός | Κανονικός | Αληθής | Ναί |
| Ηλιόλουστος | Ήπιος | Υψηλός | Ψευδής | Οχι |
| Ηλιόλουστος | Δροσερός | Κανονικός | Ψευδής | Ναί |
| Βροχερός | Ήπιος | Κανονικός | Ψευδής | Ναί |
| Ηλιόλουστος | Ήπιος | Κανονικός | Αληθής | Ναί |
| Νεφελώδης | Ήπιος | Υψηλός | Αληθής | Ναί |
| Νεφελώδης | Ζεστό | Κανονικός | Ψευδής | Ναί |
| Βροχερός | Ήπιος | Υψηλός | Αληθής | Οχι |
Η επιλογή του τένις εξαρτάται από τα τέσσερα επιχειρήματα που παρουσιάζονται εδώ.

Ένα μοντέλο Naïve Bayes μπορεί να βρει ξανά στοιχεία για το σωστό αποτέλεσμα.
Το αποτέλεσμα αυτού του παραδείγματος εκμάθησης τεχνητής νοημοσύνης είναι μια απόφαση για το αν θα παίξετε τένις, δεδομένων των καιρικών συνθηκών (τα στοιχεία). Η χρήση μόνο της προοπτικής (ηλιόλουστη, συννεφιασμένη ή βροχερή) δεν θα είναι αρκετή, επειδή η θερμοκρασία και η υγρασία μπορεί να είναι πολύ υψηλές ή ο άνεμος μπορεί να είναι δυνατός. Αυτά τα ορίσματα αντιπροσωπεύουν πραγματικές συνθήκες που έχουν πολλαπλές αιτίες ή αιτίες που συνδέονται μεταξύ τους. Ο αλγόριθμος Naïve Bayes είναι ικανός να μαντεύει σωστά όταν υπάρχουν πολλαπλές αιτίες.
Ο αλγόριθμος υπολογίζει μια βαθμολογία, με βάση την πιθανότητα λήψης μιας συγκεκριμένης απόφασης και πολλαπλασιαζόμενη με τις πιθανότητες των αποδεικτικών στοιχείων που συνδέονται με αυτήν την απόφαση. Για παράδειγμα, για να καθορίσει εάν θα παίξετε τένις όταν η προοπτική είναι ηλιόλουστη αλλά ο άνεμος είναι δυνατός, ο αλγόριθμος υπολογίζει τη βαθμολογία για μια θετική απάντηση πολλαπλασιάζοντας τη γενική πιθανότητα να παίξετε (9 παιχνίδια από τα 14 περιστατικά) με την πιθανότητα του η ημέρα είναι ηλιόλουστη (2 στους 9 αγώνες που παίχτηκαν) και οι συνθήκες ανέμου όταν παίζετε τένις (3 στους 9 αγώνες). Οι ίδιοι κανόνες ισχύουν για την αρνητική περίπτωση (η οποία έχει διαφορετικές πιθανότητες να μην παίξει υπό ορισμένες προϋποθέσεις):
πιθανότητα παιχνιδιού: 9/14 * 2/9 * 3/9 = 0,05
πιθανότητα να μην παίξετε: 5/14 * 3/5 * 3/5 = 0,13
Επειδή το σκορ για την πιθανότητα είναι υψηλότερο, ο αλγόριθμος αποφασίζει ότι είναι ασφαλέστερο να μην παίζετε κάτω από τέτοιες συνθήκες. Υπολογίζει αυτή την πιθανότητα αθροίζοντας τις δύο βαθμολογίες και διαιρώντας και τις δύο βαθμολογίες με το άθροισμά τους:
πιθανότητα παιχνιδιού : 0,05 / (0,05 + 0,13) = 0,278
πιθανότητα να μην παίξετε : 0,13 / (0,05 + 0,13) = 0,722
Μπορείτε να επεκτείνετε περαιτέρω το Naïve Bayes για να αναπαραστήσετε σχέσεις που είναι πιο περίπλοκες από μια σειρά παραγόντων που υποδηλώνουν την πιθανότητα ενός αποτελέσματος χρησιμοποιώντας ένα Bayesian δίκτυο, το οποίο αποτελείται από γραφήματα που δείχνουν πώς τα γεγονότα επηρεάζουν το ένα το άλλο. Τα γραφήματα Bayesian έχουν κόμβους που αντιπροσωπεύουν τα γεγονότα και τα τόξα που δείχνουν ποια γεγονότα επηρεάζουν άλλα, συνοδευόμενα από έναν πίνακα πιθανοτήτων υπό όρους που δείχνει πώς λειτουργεί η σχέση από την άποψη της πιθανότητας. Το σχήμα δείχνει ένα διάσημο παράδειγμα ενός Μπεϋζιανού δικτύου που λήφθηκε από μια ακαδημαϊκή εργασία του 1988, « Τοπικοί υπολογισμοί με πιθανότητες σε γραφικές δομές και η εφαρμογή τους σε έμπειρα συστήματα », από τους Lauritzen, Steffen L. και David J. Spiegelhalter, που δημοσιεύτηκε από το Journal of η Βασιλική Στατιστική Εταιρεία.

Ένα δίκτυο Bayesian μπορεί να υποστηρίξει μια ιατρική απόφαση.
Το εικονιζόμενο δίκτυο ονομάζεται Ασία. Δείχνει πιθανές καταστάσεις ασθενών και τι προκαλεί τι. Για παράδειγμα, εάν ένας ασθενής έχει δύσπνοια, μπορεί να είναι αποτέλεσμα φυματίωσης, καρκίνου του πνεύμονα ή βρογχίτιδας. Γνωρίζοντας εάν ο ασθενής καπνίζει, έχει πάει στην Ασία ή έχει ανώμαλα αποτελέσματα ακτίνων Χ (άρα δίνοντας βεβαιότητα σε ορισμένα στοιχεία, a priori στη γλώσσα Μπεϋζιανή) βοηθά να συναχθούν οι πραγματικές (μεταγενέστερες) πιθανότητες να έχει κάποια από τις παθολογίες στο γραφική παράσταση.
Τα Bayesian δίκτυα, αν και διαισθητικά, έχουν πολύπλοκα μαθηματικά πίσω τους και είναι πιο ισχυρά από έναν απλό αλγόριθμο Naïve Bayes επειδή μιμούνται τον κόσμο ως μια ακολουθία αιτιών και αποτελεσμάτων με βάση τις πιθανότητες. Τα δίκτυα Bayes είναι τόσο αποτελεσματικά που μπορείτε να τα χρησιμοποιήσετε για να αναπαραστήσετε οποιαδήποτε κατάσταση. Έχουν ποικίλες εφαρμογές, όπως ιατρικές διαγνώσεις, συγχώνευση αβέβαιων δεδομένων που προέρχονται από πολλαπλούς αισθητήρες, οικονομική μοντελοποίηση και παρακολούθηση πολύπλοκων συστημάτων όπως ένα αυτοκίνητο. Για παράδειγμα, επειδή η οδήγηση στην κυκλοφορία σε αυτοκινητόδρομο μπορεί να περιλαμβάνει περίπλοκες καταστάσεις με πολλά οχήματα, η κοινοπραξία Analysis of MassIve Data Streams (AMIDST), σε συνεργασία με την αυτοκινητοβιομηχανία Daimler, επινόησε ένα Bayesian δίκτυο που μπορεί να αναγνωρίσει ελιγμούς από άλλα οχήματα και να αυξήσει την ασφάλεια οδήγησης. Διαβάστε περισσότερα για αυτό το έργοκαι δείτε το σύνθετο δίκτυο Bayes .
Μάθετε πώς να στέλνετε προσκλήσεις στον διακομιστή Discord σας και πώς να αναπτύξετε την διαδικτυακή σας κοινότητα.
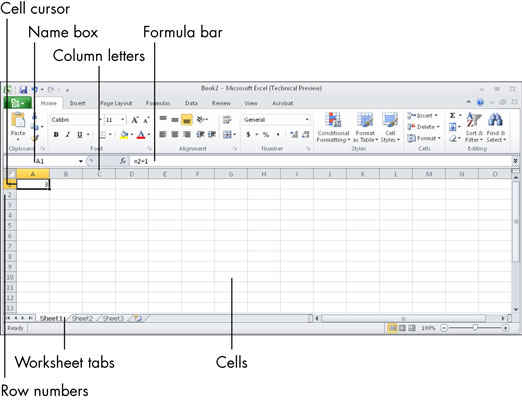
Μάθετε πώς να μετακινείστε αποτελεσματικά σε ένα φύλλο εργασίας του Microsoft Excel χρησιμοποιώντας τον δρομέα κελιού. Αυτός ο οδηγός περιλαμβάνει συντομεύσεις και χρήσιμες πληροφορίες για τη βελτιστοποίηση της εργασίας σας στο Excel.
Μάθετε πώς να μορφοποιείτε κείμενο στα μηνύματά σας στο Discord. Ακολουθήστε τις οδηγίες μας για έντονη γραφή, πλάγια γράμματα, διαγραφή και υπογράμμιση.
Μάθετε πώς να συνδέεστε με φίλους στο Discord και να παρέχετε ειδικά προνόμια σε αυτούς, όπως ανοιχτά μηνύματα και πρόσβαση σε κοινούς διακομιστές.
Ανακαλύψτε τα εργαλεία του μενού QuarkXPress Utilities για τον ορθογραφικό έλεγχο και άλλες λειτουργίες. Ιδανικό για επαγγελματίες του design και γραφίστες.
Ανακαλύψτε πώς να χρησιμοποιήσετε την αυτόματη συμπλήρωση κελιών στο OpenOffice Calc, μια δωρεάν εναλλακτική λύση στο Microsoft Office.
Ανακαλύψτε πώς να ρυθμίσετε το διάκενο παραγράφων στο Microsoft Word με τις ρυθμίσεις διάστιχου, για να επιτύχετε τέλεια μορφοποίηση στα έγγραφά σας.
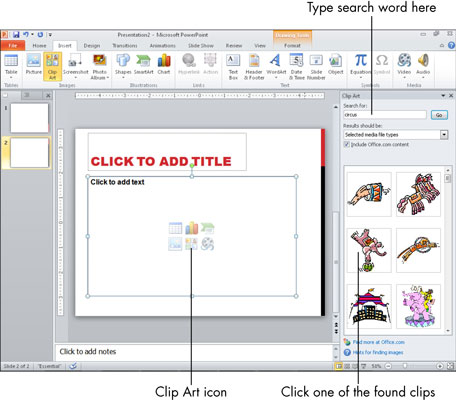
Το clip art είναι προσχεδιασμένο γενικό έργο τέχνης και η Microsoft παρέχει δωρεάν πολλά αρχεία clip art με τα προϊόντα του Office. Μπορείτε να εισαγάγετε clip art στη διάταξη διαφανειών του PowerPoint. Ο ευκολότερος τρόπος εισαγωγής clip art είναι χρησιμοποιώντας ένα από τα σύμβολα κράτησης θέσης σε μια διάταξη διαφάνειας: Εμφάνιση μιας διαφάνειας που περιέχει ένα Clip Art […]
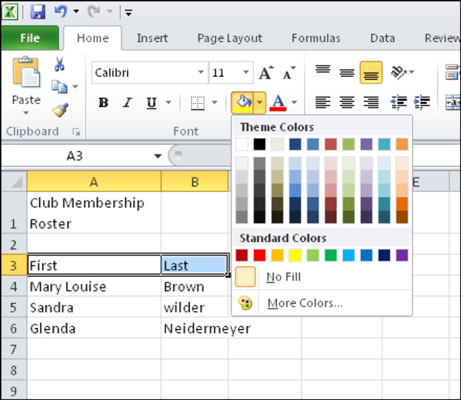
Το χρώμα πλήρωσης — που ονομάζεται επίσης σκίαση — είναι το χρώμα ή το μοτίβο που γεμίζει το φόντο ενός ή περισσότερων κελιών φύλλου εργασίας του Excel. Η εφαρμογή σκίασης μπορεί να βοηθήσει τα μάτια του αναγνώστη να ακολουθήσουν πληροφορίες σε μια σελίδα και μπορεί να προσθέσει χρώμα και οπτικό ενδιαφέρον σε ένα φύλλο εργασίας. Σε ορισμένους τύπους υπολογιστικών φύλλων, όπως ένα μητρώο βιβλιαρίου επιταγών, […]
Στο πιο απλό επίπεδο, ο κύριος σκοπός του ACT! είναι να χρησιμεύσει ως χώρος αποθήκευσης όλων των επαφών με τις οποίες αλληλεπιδράτε σε καθημερινή βάση. Μπορείτε να προσθέσετε και να επεξεργαστείτε όλες τις επαφές σας από το παράθυρο "Λεπτομέρειες επαφών" επειδή περιέχει όλες τις πληροφορίες που σχετίζονται με μια συγκεκριμένη εγγραφή και […]