Jak normalizovat pole NumPy: Rychlý průvodce

Pokud jste pracovali s Pythonem pro analýzu dat nebo strojové učení, pravděpodobně jste narazili na pole NumPy. Jsou mocným nástrojem pro práci s numerickými daty, ale někdy je třeba data v těchto polích upravit nebo „normalizovat“, aby je bylo možné efektivně použít ve vašich algoritmech. Ale co to znamená normalizovat pole?

Chcete-li normalizovat pole NumPy, musíte upravit hodnoty v poli tak, aby spadaly do určitého rozsahu, obvykle mezi 0 a 1, nebo aby měly standardní normální rozdělení s průměrem 0 a směrodatnou odchylkou 1. To se často provádí v oblasti strojového učení a analýzy dat, aby bylo zajištěno, že všechny vstupní funkce mají stejný rozsah.

V tomto článku prozkoumáme, jak můžete normalizovat pole NumPy v Pythonu. Podíváme se na různé metody, které můžete použít k normalizaci pole NumPy, a také se podíváme na příklady, které vám pomohou lépe porozumět konceptu.

Jdeme do toho!

Obsah

• Jaké jsou základy normalizace v Pythonu?
  • Co je normalizace?
  • Proč je normalizace důležitá?
  • Co jsou normy?
  • Co je normalizace ve strojovém učení?
• Jaké jsou techniky normalizace v Pythonu?
  • 1. Jak provést Min-Max Scaling
  • 2. Jak provést normalizaci L1
  • 3. Jak provést normalizaci L2
• Jak používat Scikit-Learn pro normalizaci v Pythonu
  • 1. Jak normalizovat pole pomocí MinMaxScaler
  • 2. Jak provést normalizaci řádků na místě
• Závěrečné myšlenky

Jaké jsou základy normalizace v Pythonu?

Než implementujeme normalizaci v Pythonu, musíte pochopit, co normalizace znamená.

Proto si v této části projdeme, co je normalizace a její základní koncepty.

Co je normalizace?

Normalizace je proces, který škáluje a transformuje data do standardizovaného rozsahu. To se provádí rozdělením každého prvku dat parametrem . Parametr může být maximální hodnota, rozsah nebo nějaká jiná norma.

Pole NumPy můžete normalizovat pomocí euklidovské normy (známé také jako norma L2). Kromě toho můžete také normalizovat pole NumPy změnou měřítka hodnot mezi určitým rozsahem, obvykle 0 až 1.

V Pythonu poskytuje knihovna NumPy efektivní způsob normalizace polí. To zahrnuje také vícerozměrná pole a matice.

Proč je normalizace důležitá?

Normalizace je důležitá, protože zajišťuje, že se s různými funkcemi při porovnávání a analýze dat zachází stejně. Můžete jej použít k odstranění potenciálních zkreslení nebo nesrovnalostí, které mohou vzniknout v důsledku různých měřítek.

Co jsou normy?

Parametr, který použijete pro normalizaci, mohou být různé normy , například euklidovská norma (L2), manhattanská norma (L1) nebo maximální norma (L_inf). Normy se používají k výpočtu velikosti vektoru nebo matice . Ty se pak použijí jako faktor měřítka k normalizaci dat.

Při práci s maticemi často používáme Frobeniovu normu , což je zobecnění euklidovské normy pro vícerozměrná pole.

Následující příklad ukazuje normalizaci matice pomocí Frobeniovy normy:

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Calculate the Frobenius norm
frobenius_norm = np.linalg.norm(matrix, 'fro')

# Normalize the matrix
normalized_matrix = matrix / frobenius_norm

print('Original Matrix:')
print(matrix)
print('nFrobenius Norm:')
print(frobenius_norm)
print('nNormalized Matrix:')
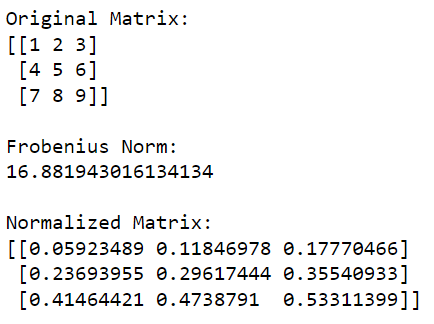
print(normalized_matrix)

Tento kód Pythonu nejprve importuje knihovnu NumPy a použije ji k vytvoření matice. Poté vypočítá Frobeniovu normu matice a poté vydělí každý prvek v matici touto hodnotou, aby ji normalizoval.

Výstup tohoto kódu je uveden níže:

Co je normalizace ve strojovém učení?

Ve strojovém učení je normalizace důležitým krokem předzpracování, protože zlepšuje výkon algoritmů.

Při provádění technik optimalizace založených na přechodech zjistíte, že optimalizované funkce mají tendenci konvergovat rychleji a efektivněji. To proto, že snižuje riziko špatného měřítka nebo mizejících přechodů.

Jaké jsou techniky normalizace v Pythonu?

Normalizaci polí můžete provádět mnoha způsoby. Některé metody jsou však populárnější než jiné díky své vysoké účinnosti.

V této části se podíváme na tři široce používané normalizační techniky:

1. Min-Max škálování

2. Normalizace L1

3. Normalizace L2

1. Jak provést Min-Max Scaling

Minimální a maximální škálování je také známé jako lineární normalizace nebo škálování prvků. V min-max škálování škálujeme hodnoty pole NumPy tak, aby spadaly do určeného rozsahu, obvykle mezi 0 a 1.

Chcete-li to provést, odečtěte minimální hodnotu od každého prvku a vydělte výsledek rozdílem mezi maximální a minimální hodnotou.

Min-max měřítko můžete matematicky znázornit jako:

x' = (x - min(x)) / (max(x) - min(x))

Následující příklad ukazuje, jak můžete provést min-max škálování pomocí knihovny NumPy:

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform min-max scaling
min_val = np.min(matrix)
max_val = np.max(matrix)

scaled_matrix = (matrix - min_val) / (max_val - min_val)

print('Original Matrix:')
print(matrix)
print('nMin-Max Scaled Matrix:')
print(scaled_matrix)

Tento kód nejprve naimportuje NumPy a poté vypočítá minimální a maximální hodnoty v matici, kterou pak upraví tak, aby všechny hodnoty byly mezi 0 (odpovídající původní minimální hodnotě) a 1 (odpovídající původní maximální hodnotě).

Výstup tohoto kódu je uveden níže:

Min-max škálování je velmi běžná forma škálování ve strojovém učení a předzpracování dat.

2. Jak provést normalizaci L1

Normalizace L1 využívá normu L1, což je součet absolutních hodnot prvků pole. To je užitečné zejména pro řídké matice. Zajišťuje, že součet absolutních hodnot prvků normalizovaného pole se rovná 1.

Vzorec pro normalizaci L1 je:

x' = x / sum(|x|)

Následující příklad ukazuje, jak můžete provést normalizaci L1 pomocí NumPy:

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform L1 normalization
l1_norm = np.linalg.norm(matrix, 1, axis=1, keepdims=True)
l1_normalized_matrix = matrix / l1_norm

print('Original Matrix:')
print(matrix)
print('nL1 Normalized Matrix:')
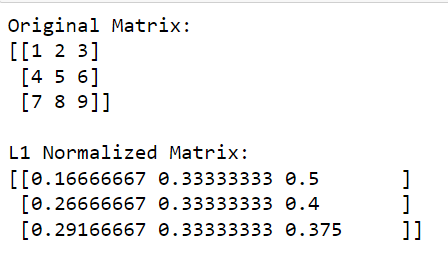
print(l1_normalized_matrix)

V tomto kódu np.linalg.norm (matice, 1, osa=1, keepdims=True) vypočítá normu L1 pro každý řádek (toto se provede zadáním osy=1).

Tato operace vrátí sloupcový vektor, kde každý prvek je normou L1 odpovídajícího řádku. Vydělením původní matice těmito normami (provedením dělení po prvcích) získáme L1 normalizovanou verzi matice.

Výstup je uveden níže:

3. Jak provést normalizaci L2

Normalizace L2 používá normu L2, což je druhá odmocnina součtu prvků čtvercového pole.

Tato metoda převádí normalizované pole na jednotkový vektor s 2-normou 1. Normalizace L2 je užitečná pro zmenšení rozměrů a zajišťuje stejnou důležitost pro všechny funkce.

Vzorec pro normalizaci L2 je:

x' = x / sqrt(sum(x^2))

Takto můžete provést normalizaci L2 pomocí NumPy :

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform L2 normalization
l2_norm = np.linalg.norm(matrix, 2, axis=1, keepdims=True)
l2_normalized_matrix = matrix / l2_norm

print('Original Matrix:')
print(matrix)
print('nL2 Normalized Matrix:')
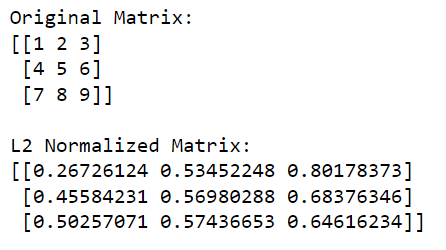
print(l2_normalized_matrix)

V tomto kódu np.linalg.norm(matice, 2, osa=1, keepdims=True) vypočítá normu L2 (euklidovská norma) pro každý řádek (toto se provede zadáním osy=1). Tato operace vrátí sloupcový vektor, kde každý prvek je normou L2 odpovídajícího řádku.

Vydělením původní matice těmito normami (provedením dělení po prvcích) získáme L2 normalizovanou verzi matice.

Výstup je uveden níže:

Dobře, teď, když jsme prošli populární způsoby, jak vytvořit normalizované pole pomocí NumPy, pojďme se v další části podívat na to, jak můžete udělat totéž pomocí jiných knihoven Pythonu.

Jak používat Scikit-Learn pro normalizaci v Pythonu

Scikit-learn je výkonná Python knihovna pro strojové učení. Poskytuje několik nástrojů pro předzpracování dat.

Jedním z nástrojů, který můžete použít, je modul sklearn.preprocessing , který nabízí různé techniky k provádění normalizace. K dispozici je mnoho různých funkcí scaleru, transformátorů a normalizátorů. My se však zaměříme na MinMaxScaler a normalize .

K předzpracování dat pomocí scikit-learn používáte hlavně rozhraní API transformátoru. To zahrnuje metody fit , transform a fit_transform .

1. Jak normalizovat pole pomocí MinMaxScaler

MinMaxScaler je scaler, který normalizuje data na zadaný rozsah, obvykle [0, 1] .

Vzorec pro MinMaxScalar je uveden níže:

scaled_value = (value - min_value) / (max_value - min_value)

Chcete-li implementovat MinMaxScaler , můžete postupovat takto:

1. Importujte požadované knihovny:

   import numpy as np
   from sklearn.preprocessing import MinMaxScaler

2. Vytvořte pole NumPy:

   data = np.array([[1., 2., 5.], [3., 6., 8.], [5., 10., 12.]])

3. Vytvořte instanci MinMaxScaler a přizpůsobte jej datům:

   scaler = MinMaxScaler()
   scaler.fit(data)

4. Transformujte data pomocí metody transform nebo fit_transform :

   normalized_data = scaler.transform(data)

Výstup tohoto kódu je uveden níže:

Jak můžete vidět na výstupu, MinMaxScalarMatrix má pouze hodnoty v rozmezí od 0 do 1.

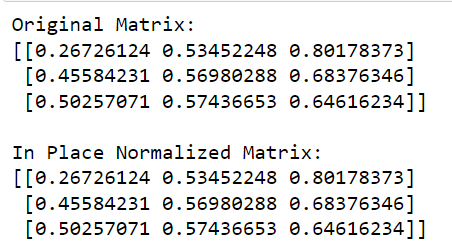
2. Jak provést normalizaci řádků na místě

Jako alternativu můžete také použít místní normalizaci řádků pomocí funkce normalizace .

Tato metoda normalizuje každé vstupní pole nebo prvek nezávisle změnou měřítka vektoru na jednotkovou normu. Ve výchozím nastavení používá funkce normalizace normu L2 k provedení jednoduché normalizace, ale můžete si vybrat i jiné možnosti normy.

Následující příklad ukazuje normalizaci řádků na místě:

from sklearn.preprocessing import normalize
import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]], dtype=float)

# Apply in-place row normalization
normalize(matrix, norm='l2', copy=False)

print('L2 Normalized Matrix:')
print(matrix)

V tomto kódu zavoláme funkci normalizace ze sklearn , definujeme normu, která se má použít (v tomto případě 'l2') a nastavíme copy=False , abychom provedli normalizaci na místě.

Výstup tohoto kódu je uveden níže:

Chcete-li se dozvědět více o strojovém učení v , podívejte se na následující video:

Závěrečné myšlenky

Když budete dále prozkoumávat datovou vědu a strojové učení, zjistíte, že proces normalizace je nezbytným krokem ve vašem kanálu předběžného zpracování dat.

Za prvé klade různé rysy na společnou stupnici. Díky tomu jsou vaše modely méně citlivé na rozsah vstupů. Může výrazně zlepšit výkon mnoha algoritmů strojového učení.

Za druhé vám pomůže urychlit tréninkový proces. Některé algoritmy, zejména ty, které jsou založeny na vypočítaných výpočtech vzdálenosti, konvergují rychleji, když jsou data normalizována.

Tím, že se naučíte normalizovat data, získáte zásadní dovednost. Normalizace je praktický nástroj běžně používaný v aplikacích reálného světa. Pomůže vám snížit pravděpodobnost neočekávaných výsledků v důsledku odlehlých hodnot nebo rozdílů v jednotkách.

Jako každý nástroj spočívá klíč ke zvládnutí normalizace v praxi. Neváhejte si tedy ušpinit ruce a experimentovat s různými datovými sadami a náhodnými hodnotami. Svět je vaše ústřice. Šťastné kódování!